安徽省六安市三校2022-2023学年数学七年级第二学期期末学业质量监测模拟试题含答案

安徽省六安市三校2022-2023学年数学七年级第二学期期末学业质量监测模拟试题

（时间：120分钟             分数：120分）

学校_______            年级_______        姓名_______

注意事项

1．考试结束后，请将本试卷和答题卡一并交回．

2．答题前，请务必将自己的姓名、准考证号用0．5毫米黑色墨水的签字笔填写在试卷及答题卡的规定位置．

3．请认真核对监考员在答题卡上所粘贴的条形码上的姓名、准考证号与本人是否相符．

4．作答选择题，必须用2B铅笔将答题卡上对应选项的方框涂满、涂黑；如需改动，请用橡皮擦干净后，再选涂其他答案．作答非选择题，必须用05毫米黑色墨水的签字笔在答题卡上的指定位置作答，在其他位置作答一律无效．

5．如需作图，须用2B铅笔绘、写清楚，线条、符号等须加黑、加粗．

一、选择题：本大题共12个小题，每小题3分，共36分.在每小题给出的四个选项中，只有一项是符合题目要求的.

1．下列各式从左到右的变形中，是因式分解的为（  ）

A． B．

C． D．

2．给出下列几组数：① 4,5,6；②8，15，16;③n2－1，2n，n2＋1；④m2－n2，2mn，m2＋n2（m>n>0）．其中—定能组成直角三角形三边长的是（    ）．

A．①②    B．③④    C．①③④    D．④

3．如图，菱形ABCD中，AB=4，E，F分别是AB、BC的中点，P是AC上一动点，则PF+PE的最小值是（   ）

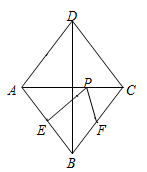
A．3 B． C．4 D．

4．下列数据中不能作为直角三角形的三边长是（　　）

A．1、1、 B．5、12、13 C．3、5、7 D．6、8、10

5．如图，在△ABC中，∠C＝90°，AD平分∠BAC交BC于点D，且BD＝2CD，BC＝9cm，则点D到AB的距离为（　　）

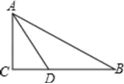
A．3cm B．2cm C．1cm D．4.5cm

6．对于反比例函数，下列说法不正确的是（    ）

A．点在它的图像上 B．当时，随的增大而增大

C．它的图像在第二、四象限 D．当时，随的增大而减小

7．如图，小明同学用自制的直角三角形纸板测量树的高度，他调整自己的位置，设法使斜边保持水平，并且边与点在同一直线上.已知纸板的两条直角边，，测得边离地面的高度，，则树高是（    ）

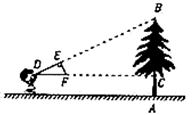
A．4米 B．4.5米 C．5米 D．5.5米

8．七名学生在一分钟内的跳绳个数分别是：150、140、100、110、130、110、120，设这组数据的平均数是a，中位数是b，众数是c，则有（ ）

A．c>b>a B．b>c>a C．c>a>b D．a>b>c

9．下列命题中，不正确的是（ ）．

A．一个四边形如果既是矩形又是菱形，那么它一定是正方形

B．有一个角是直角，且有一组邻边相等的平行四边形是正方形

C．有一组邻边相等的矩形是正方形

D．两条对角线垂直且相等的四边形是正方形

10．若a是（﹣4）2的平方根，b的一个平方根是2，则a+b的立方根为（　　）

A．0 B．2 C．0或2 D．0或﹣2

11．关于直线的说法正确的是（）

A．图像经过第二、三、四象限 B．与轴交于

C．与轴交于 D．随增大而增大

12．2022年将在北京---张家口举办冬季奥运会，很多学校开设了相关的课程.某校8名同学参加了滑雪选修课，他们被分成甲、乙两组进行训练，身高（单位：cm）如下表所示：

设两队队员身高的平均数依次为，，方差依次为，，则下列关系中完全正确的是（    ）.

A． B．

C． D．

二、填空题（每题4分，满分20分，将答案填在答题纸上）

13．方程x3=8的根是______．

14．一组数据3，2，4，5，2的众数是______．

15．＝   ▲   ．

16．如图，在矩形ABCD中，AB＝1，BC＝7，将矩形ABCD绕点C逆时针旋转90°得到矩形A′B′CD′，点E、F分别是BD、B′D′的中点，则EF的长度为________cm．

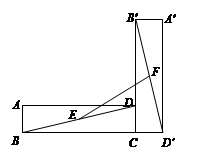
17．已知一个直角三角形的两边长分别为12和5，则第三条边的长度为_______

三、解答题 （本大题共7小题，共64分.解答应写出文字说明、证明过程或演算步骤.）

18．（5分）我们知道：等腰三角形两腰上的高相等．

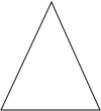
（1）请你写出它的逆命题：______．

（2）逆命题是真命题吗？若是，请证明；若不是，请举出反例（要求：画出图形，写出已知，求证和证明过程）．

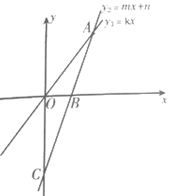
19．（5分）如图，正比例函数y1=kx与-次函数y2=mx+n的图象交于点A(3，4)，一次函数y2的图象与x轴，y轴分别交于点B，点C，且0A=OC．

(1)求这两个函数的解析式；

(2)求直线AB与两坐标轴所围成的三角形的面积．

20．（8分）一家蔬菜公司收购到某种绿色蔬菜140吨，准备加工后进行销售，销售后获利的情况如下表所示：

已知该公司的加工能力是：每天能精加工5吨或粗加工15吨，但两种加工不能同时进行.受季节等条件的限制，公司必须在一定时间内将这批蔬菜全部加工后销售完.

（1）如果要求12天刚好加工完140吨蔬菜，则公司应安排几天精加工，几天粗加工？

（2）如果先进行精加工，然后进行粗加工.

①试求出销售利润元与精加工的蔬菜吨数之间的函数关系式；

②若要求在不超过10天的时间内，将140吨蔬菜全部加工完后进行销售，则加工这批蔬菜最多获得多少利润？此时如何分配加工时间？

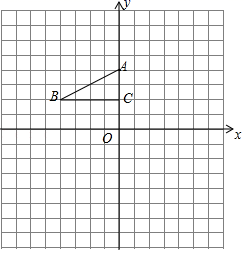
21．（10分）如图，方格纸中每个小正方形的边长都是1个单位长度，Rt△ABC的三个顶点分别为A（0，4），B（﹣4，2），C（0，2）．

（1）画△A1B1C1，使它与△ABC关于点C成中心对称；

（2）平移△ABC，使点A的对应点A2坐标为（﹣2，4），画出平移后对应的△A2B2C2；

（3）若将△A1B1C1绕点P旋转可得到△A2B2C2，请直接写出旋转中心P的坐标．

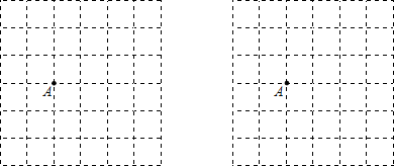
22．（10分）如图，在6×6的网格中，每个小正方形的边长为1，点A在格点（小正方形的顶点）上，试在各网格中画出顶点在格点上，面积为6，且符合相应条件的图形

（1）以A为顶点的平行四边形；

（2）以A为对角线交点的平行四边形．

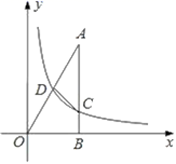
23．（12分）如图，的直角边OB在x轴的正半轴上，反比例函数的图象经过斜边OA的中点D,与直角边AB相交于点C.

①若点，求点C的坐标：

②若，求k的值.

参考答案

一、选择题：本大题共12个小题，每小题3分，共36分.在每小题给出的四个选项中，只有一项是符合题目要求的.

1、D

2、D

3、C

4、C

5、A

6、D

7、D

8、D

9、D

10、C

11、B

12、D

二、填空题（每题4分，满分20分，将答案填在答题纸上）

13、2

14、1

15、1．

16、5

17、13或；

三、解答题 （本大题共7小题，共64分.解答应写出文字说明、证明过程或演算步骤.）

18、（1）两边上的高相等的三角形是等腰三角形；（2）是，证明见解析．

19、 (1) ，；(2) .

20、（1）应安排4天进行精加工，8天进行粗加工

（2）①=

②安排1天进行精加工，9天进行粗加工，可以获得最多利润为元

21、（1）见解析；（2）见解析；（3）P（﹣1，2）

22、（1）见解析；（2）见解析

23、①（4，）；②k=12