安徽省宿州市时村中学2022-2023学年七年级数学第二学期期末考试试题含答案

这是一份安徽省宿州市时村中学2022-2023学年七年级数学第二学期期末考试试题含答案，共8页。试卷主要包含了函数中，自变量x的取值范围是，下列各组数中，不是勾股数的是等内容，欢迎下载使用。
安徽省宿州市时村中学2022-2023学年七年级数学第二学期期末考试试题（时间：120分钟             分数：120分） 学校_______            年级_______        姓名_______ 请考生注意：1．请用2B铅笔将选择题答案涂填在答题纸相应位置上，请用0．5毫米及以上黑色字迹的钢笔或签字笔将主观题的答案写在答题纸相应的答题区内。写在试题卷、草稿纸上均无效。2．答题前，认真阅读答题纸上的《注意事项》，按规定答题。 一、选择题(每小题3分,共30分)1．已知一次函数y=kx+b（k≠0）的图象如图所示，则不等式kx+b＞1的解集为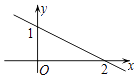（   ）  A．x＜0 B．x＞0 C．x＜2 D．x＞22．如图，在直线l上有三个正方形m、q、n，若m、q的面积分别为5和11，则n的面积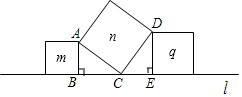（　　）A．4 B．6 C．16 D．553．如图，已知△ABC为直角三角形，∠B=90°，若沿图中虚线剪去∠B，则∠1+∠2=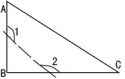（    ）A．90° B．135° C．270° D．315°4．如图，在斜坡的顶部有一铁塔AB，B是CD的中点，CD是水平的，在阳光的照射下，塔影DE留在坡面上．已知铁塔底座宽CD＝12 m，塔影长DE＝18 m，小明和小华的身高都是1.6m，同一时刻，小明站在点E处，影子在坡面上，小华站在平地上，影子也在平地上，两人的影长分别为2m和1m，那么塔高AB为(　　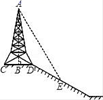)A．24m B．22m C．20m D．18m5．函数中，自变量x的取值范围是（ ）A．x＞1 B．x＜1 C． D．6．一次函数满足，且随的增大而减小，则此函数的图象不经过（ ）A．第一象限 B．第二象限 C．第三象限 D．第四象限7．如图，若正比例函数y＝kx图象与四条直线x＝1，x＝2，y＝1，y＝2相交围成的正方形有公共点，则k的取值范围是(　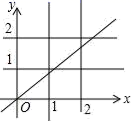　)A．k≤2 B．k≥ C．0＜k＜ D．≤k≤28．下列各组数中，不是勾股数的是 （  ）A．3，4，5 B．5，12，13 C．6，8，10 D．7，13，189．如图，在平行四边形ABCD中，∠A＝40°，则∠C大小为( 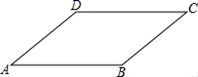  )A．40° B．80° C．140° D．180°10．某校规定学生的学期数学成绩满分为100分，其中研究性学习成绩占40%，期末卷面成绩占60%，小明的两项成绩（百分制）依次是80分，90分，则小明这学期的数学成绩是（ ）A．80分 B．82分 C．84分 D．86分二、填空题(本大题共有6小题，每小题3分，共18分)11．如图，直线与双曲线交于A、B两点，过点A作轴，垂足为M，连结BM，若，则k的值是______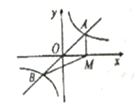．12．如果关于x的方程bx2=2有实数解，那么b的取值范围是_____．13．如图，过矩形ABCD的对角线BD上一点K分别作矩形两边的平行线MN与PQ，那么图中矩形AMKP的面积S1与矩形QCNK的面积S2的大小关系是S1_____S2；（填“＞”或“＜”或“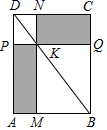＝”）14．如图，在RtACB中，∠C＝90°，AB＝2，以点B为圆心，适当长为半径画弧，分别交边AB，BC于点E，F，再分别以点E，F为圆心，大于EF的长为半径画弧，两弧相交于点P，作射线BP交AC于点D，若CD＝1，则ABD的面积为_____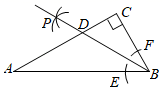．15．如图，已知菱形OABC的顶点O(0，0)，B(2，2)，则菱形的对角线交点D的坐标为(1,1),若菱形绕点O逆时针旋转，每秒旋转45°，则第60秒时，点D的坐标为________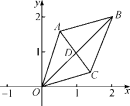．16．已知一次函数y=x+2与一次函数y=mx+n的图象交于点P（a，-2），则关于x的方程x+2=mx+n的解是__________．三、解下列各题(本大题共8小题，共72分)17．（8分）暑假期间某景区商店推出销售纪念品活动，已知纪念品每件的进货价为30元，经市场调研发现，当该纪念品的销售单价为40元时，每天可销售280件；当销售单价每增加1元，每天的销售数量将减少10件. （销售利润=销售总额-进货成本） （1）若该纪念品的销售单价为45元时则当天销售量为______件。 （2）当该纪念品的销售单价为多少元时，该产品的当天销售利润是2610元。 （3）该纪念品的当天销售利润有可能达到3700元吗？若能，请求出此时的销售单价；若不能，请说明理由。   18．（8分）计算：（+）×﹣4   19．（8分）如图1，在中，，，，动点P从点A开始沿边AC向点C以每秒1个单位长度的速度运动，动点Q从点C开始沿边CB向点B以每秒2个单位长度的速度运动，过点P作，交AB于点D，连接PQ，点P、Q分别从点A、C同时出发，当其中一点到达端点时，另一点也随之停止运动，设运动时间为t秒．直接用含t的代数式分别表示：______，______；是否存在t的值，使四边形PDBQ为平行四边形？若存在，求出t的值；若不存在，说明理由．如图2，在整个运动过程中，求出线段PQ中点M所经过的路径长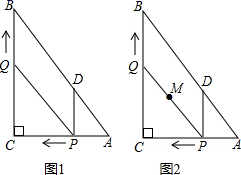．   20．（8分）某单位欲从内部招聘管理人员一名，对甲、乙、丙三名候选人进行了笔试和面试两项测试，三人的测试成绩如下表所示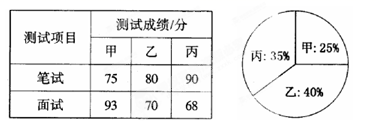：    根据录用程序，组织200名职工对三人利用投票推荐的方式进行民主评议，三人得票率（没有弃权票，每位职工只能推荐1人）如上图所示，每得一票记作1分． （l）请算出三人的民主评议得分； （2）如果根据三项测试的平均成绩确定录用人选，那么谁将被录用（精确到 0.01 )? （3）根据实际需要，单位将笔试、面试、民主评议三项测试得分按 4 : 3 : 3 的比例确定个人成绩，那么谁将被录用？   21．（8分）用适当方法解方程：（1）（2）   22．（10分）将矩形ABCD绕点B顺时针旋转得到矩形A1BC1D1，点A、C、D的对应点分别为A1、C1、D1（1）当点A1落在AC上时①如图1，若∠CAB＝60°，求证：四边形ABD1C为平行四边形；②如图2，AD1交CB于点O．若∠CAB≠60°，求证：DO＝AO；（2）如图3，当A1D1过点C时．若BC＝5，CD＝3，直接写出A1A的长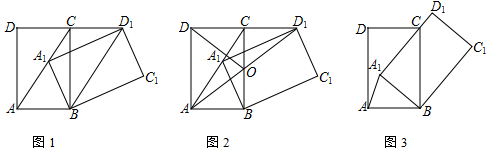．   23．（10分）某学习小组在学习了函数及函数图象的知识后，想利用此知识来探究周长一定的矩形其边长分别为多少时面积最大. 请将他们的探究过程补充完整.（1）列函数表达式：若矩形的周长为8，设矩形的一边长为x，面积为y，则有y=____________；（2）上述函数表达式中，自变量x的取值范围是____________；（3）列表：x…0.511.522.533.5…y…1.7533.7543.753m… 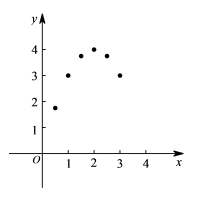        写出m=____________；（4）画图：在平面直角坐标系中已描出了上表中部分各对应值为坐标的点，请你画出该函数的图象；（5）结合图象可得，x=____________时，矩形的面积最大；写出该函数的其它性质（一条即可）：____________.   24．（12分）某校七、八年级各有学生400人，为了解这两个年级普及安全教育的情况，进行了抽样调查，过程如下选择样本,收集数据从七、八年级各随机抽取20名学生,进行安全教育考试,测试成绩(百分制)如下：七年级 85 79 89 83 89 98 68 89 79 5999  87  85  89  97  86  89  90  89  77八年级 71  94  87  92  55  94  98  78  86  9462  99  94  51  88  97  94  98  85  91分组整理，描述数据(1)按如下频数分布直方图整理、描述这两组样本数据，请补全八年级20名学生安全教育频数分布直方图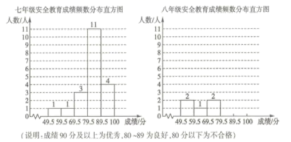；(2)两组样本数据的平均数、中位数、众数、优秀率如下表所示，请补充完整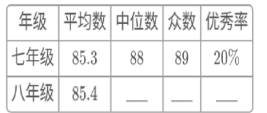；得出结论，说明理由. (3)整体成绩较好的年级为___,理由为___(至少从两个不同的角度说明合理性).   参考答案 一、选择题(每小题3分,共30分)1、A2、C3、C4、A5、C6、A7、D8、D9、A10、D 二、填空题(本大题共有6小题，每小题3分，共18分)11、112、b＞1．13、=14、15、 (－1，－1)16、x=-4 三、解下列各题(本大题共8小题，共72分)17、（1）1．（2）当该纪念品的销售单价为2元时，该产品的当天销售利润是2613元．（3）不能，理由见解析.18、 19、（1），；（2）详见解析；（3）220、 (l) 50 分，80 分，70 分(2)候选人乙将被录用（3）候选人丙将被录用21、（１）x1=1+，x2=1−；（２）x1=-1,x2=1．22、（1）①证明见解析；②证明见解析；（2）23、见解析24、（1）见解析；（2）91.5，94，55%；（3）八年级，八年级的中位数和优秀率都高于七年级.