山东单县北城三中联考2022-2023学年七下数学期末监测试题含答案

山东单县北城三中联考2022-2023学年七下数学期末监测试题

（时间：120分钟             分数：120分）

学校_______            年级_______        姓名_______

考生请注意：

1．答题前请将考场、试室号、座位号、考生号、姓名写在试卷密封线内，不得在试卷上作任何标记。

2．第一部分选择题每小题选出答案后，需将答案写在试卷指定的括号内，第二部分非选择题答案写在试卷题目指定的位置上。

3．考生必须保证答题卡的整洁。考试结束后，请将本试卷和答题卡一并交回。

一、选择题：本大题共12个小题，每小题3分，共36分.在每小题给出的四个选项中，只有一项是符合题目要求的.

1．如图，将△ABC绕点A顺时针旋转，使点C落在边AB上的点E处，点B落在点D处，连结BD，如果∠DAC=∠DBA，那么∠BAC度数是（    ）

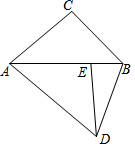
A．32° B．35° C．36° D．40°

2．若a＞b，则下列式子正确的是（　　）

A．a+2＜b+2 B．﹣2a＞﹣2b C．a﹣2＞b﹣2 D．

3．已知点和点在函数的图像上，则下列结论中正确的（）

A． B． C． D．

4．有一组数据：3，3，5，6，1．这组数据的众数为（　　）

A．3 B．5 C．6 D．1

5．如图，△ABC三边的长分别为3、4、5，点D、E、F分别是△ABC各边中点，则△DEF的周长和面积分别为        （   ）

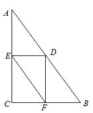
A．6，3 B．6，4 C．6， D．4，6

6．若点P（a，2）在第二象限，则a的值可以是（　　）

A． B．0 C．1 D．2

7．已知不等式组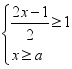的解集是x≥2，则a的取值范围是(   )

A．a＜2 B．a＝2 C．a＞2 D．a≤2

8．如图，，要根据“”证明，则还要添加一个条件是(     )

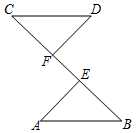
A． B． C． D．

9．某校九年级（1）班全体学生2018年初中毕业体育考试的成绩统计如表：

根据表中的信息判断，下列结论中错误的是（　　）

A．该班一共有45名同学

B．该班学生这次考试成绩的众数是28

C．该班学生这次考试成绩的平均数是25

D．该班学生这次考试成绩的中位数是28

10．如图，在平面直角坐标系中，等边△OAB的顶点B的坐标为(2，0)，点A在第一象限内，将△OAB沿直线OA的方向平移至△O′A′B′的位置，此时点A′的横坐标为3，则点B′的坐标为(     )

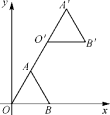
A．(4，2) B．(3，3) C．(4，3) D．(3，2)

11．如图，正方形中，，是的中点，是上的一动点，则的最小值是（    ）

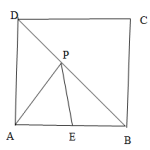
A．2 B．4 C． D．

12．为了解学生的体能情况，抽取某学校同年级学生进行跳绳测试，将所得数据整理后，画出如图所示的频数分布直方图．已知图中从左到右前三个小组的频率分别为0.1，0.3，0.4，第一小组的频数为5，则第四小组的频数为（      ）

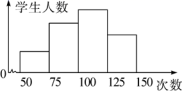
A．5

B．10

C．15

D．20

二、填空题（每题4分，满分20分，将答案填在答题纸上）

13．写出一个图象经过一，三象限的正比例函数y=kx（k≠0）的解析式（关系式）  ．

14．分式与的最简公分母是__________．

15．若关于的方程的一个根是，则方程的另一个根是________．

16．已知1＜x＜5，化简+|x-5|=____．

17．若，则________．

三、解答题 （本大题共7小题，共64分.解答应写出文字说明、证明过程或演算步骤.）

18．（5分）如图，BD为平行四边形ABCD的对角线，按要求完成下列各题．

（1）用直尺和圆规作出对角线BD的垂直平分线交AD于点E，交BC于点F，垂足为O，（保留作图痕迹，不要求写作法）

（2）在（1）的基础上，连接BE和DF，求证：四边形BFDE是菱形．

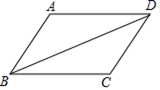
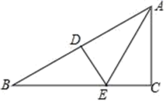
19．（5分）如图，在△ABC中，∠B＝30°，边AB的垂直平分线分别交AB和BC于点D，E，且AE平分∠BAC．

（1）求∠C的度数；

（2）若CE＝1，求AB的长．

20．（8分）为了了解高峰时段37路公交车从总站乘该路车出行的人数，随机抽查了10个班次乘该路车人数，结果如下：16，25，18，1，25，30，28，29，25，1．

(1)请求出这10个班次乘该路车人数的平均数、众数与中位数；

(2)如果37路公交车在高峰时段从总站共发出50个班次，根据上面的计算结果，估计在高峰时段从总站乘该路车出行的乘客共有多少人？

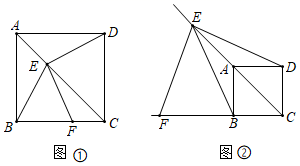
21．（10分）感知：如图①，在正方形中，点在对角线上（不与点、重合），连结、，过点作，交边于点.易知，进而证出.

探究：如图②，点在射线上（不与点、重合），连结、，过点作，交的延长线于点.求证：.

应用：如图②，若，，则四边形的面积为________.

22．（10分）如图1，在矩形ABCD中，对角线AC与BD相交于点O，过点O作直线EF⊥BD，且交AC于点E，交BC于点F，连接BE、DF，且BE平分∠ABD.

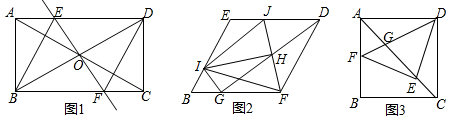
（1）①求证：四边形BFDE是菱形；②求∠EBF的度数．
（2）把（1）中菱形BFDE进行分离研究，如图2，G，I分别在BF，BE边上，且BG=BI，连接GD，H为GD的中点，连接FH，并延长FH交ED于点J，连接IJ，IH，IF，IG．试探究线段IH与FH之间满足的数量关系，并说明理由；
（3）把（1）中矩形ABCD进行特殊化探究，如图3，矩形ABCD满足AB=AD时，点E是对角线AC上一点，连接DE，作EF⊥DE，垂足为点E，交AB于点F，连接DF，交AC于点G．请直接写出线段AG，GE，EC三者之间满足的数量关系．

23．（12分）如下4个图中，不同的矩形ABCD，若把D点沿AE对折，使D点与BC上的F点重合；

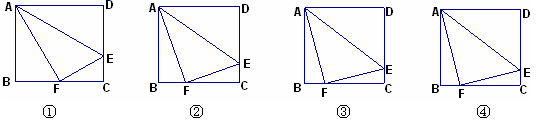
（1）图①中，若DE︰EC=2︰1，求证：△ABF∽△AFE∽△FCE；并计算BF︰FC；

（2）图②中若DE︰EC=3︰1，计算BF︰FC=     ；图③中若DE︰EC=4︰1，计算BF︰FC=     ；

（3）图④中若DE︰EC=︰1，猜想BF︰FC=       ；并证明你的结论

参考答案

一、选择题：本大题共12个小题，每小题3分，共36分.在每小题给出的四个选项中，只有一项是符合题目要求的.

1、C

2、C

3、B

4、A

5、C

6、A

7、B

8、A

9、C

10、A

11、D

12、B

二、填空题（每题4分，满分20分，将答案填在答题纸上）

13、y=2x

14、

15、-2

16、4

17、

三、解答题 （本大题共7小题，共64分.解答应写出文字说明、证明过程或演算步骤.）

18、（1）作图见解析；

（2）证明见解析.

19、（1）；（2）.

20、解：(1)平均数是25人，众数是25人，中位数是26人；(2)1250 人．

21、探究：见解析；应用：

22、（1）①证明见解析；②；（2）；（3）.

23、（1）根据折叠的性质及矩形的性质可证得△ABF∽△AFE∽△FCE，再根据相似三角形的性质求解即可，1:1；（2）1:2，1:3；（3）1︰（n-1）