


山东省威海乳山市2022-2023学年数学七下期末监测试题含答案
展开
这是一份山东省威海乳山市2022-2023学年数学七下期末监测试题含答案,共7页。试卷主要包含了考生必须保证答题卡的整洁,下列说法,你认为正确的是,下列说法正确的是等内容,欢迎下载使用。
山东省威海乳山市2022-2023学年数学七下期末监测试题(时间:120分钟 分数:120分) 学校_______ 年级_______ 姓名_______ 考生请注意:1.答题前请将考场、试室号、座位号、考生号、姓名写在试卷密封线内,不得在试卷上作任何标记。2.第一部分选择题每小题选出答案后,需将答案写在试卷指定的括号内,第二部分非选择题答案写在试卷题目指定的位置上。3.考生必须保证答题卡的整洁。考试结束后,请将本试卷和答题卡一并交回。 一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.如图,矩形ABCD的两条对角线交于点O,若![]() ,
,![]() ,则AC等于( )
,则AC等于( )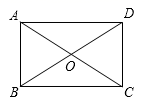 A.8 B.10 C.12 D.182.如图,四边形ABCD为菱形,AB=5,BD=8,AE⊥CD于E,则AE的长为( )
A.8 B.10 C.12 D.182.如图,四边形ABCD为菱形,AB=5,BD=8,AE⊥CD于E,则AE的长为( )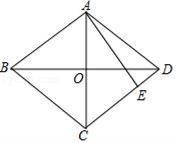 A.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 3.下列根式中,不.是.最简二次根式的是( )A.
3.下列根式中,不.是.最简二次根式的是( )A.![]() B.
B.![]() C.
C.![]() D.
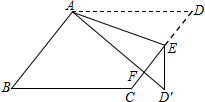
D.![]() 4.如图,在平行四边形ABCD中,E是边CD上一点,将
4.如图,在平行四边形ABCD中,E是边CD上一点,将![]() 沿AE折叠至
沿AE折叠至![]() 处,
处,![]() 与CE交于点F,若
与CE交于点F,若![]() ,
,![]() ,则
,则![]() 的度数为
的度数为![]()
![]()
 A.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 5.一个多边形的每一个内角均为
5.一个多边形的每一个内角均为![]() ,那么这个多边形是( )A.七边形 B.六边形 C.五边形 D.正方形6.下列图形中,既是轴对称图形又是中心对称图形的是
,那么这个多边形是( )A.七边形 B.六边形 C.五边形 D.正方形6.下列图形中,既是轴对称图形又是中心对称图形的是![]()
![]() A.
A. B.
B.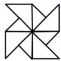 C.
C.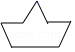 D.
D.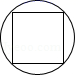 7.下列说法,你认为正确的是( )A.0 的倒数是 0 B.3-1=-3 C.是有理数 D.
7.下列说法,你认为正确的是( )A.0 的倒数是 0 B.3-1=-3 C.是有理数 D.![]() 38.下列说法正确的是( )A.顺次连接任意一个四边形四边的中点,所得到的四边形一定是平行四边形B.平行四边形既是中心对称图形,又是轴对称图形C.对角线相等的四边形是矩形D.只要是证明两个直角三角形全等,都可以用“HL”定理9.如图,在平面直角坐标系中,点
38.下列说法正确的是( )A.顺次连接任意一个四边形四边的中点,所得到的四边形一定是平行四边形B.平行四边形既是中心对称图形,又是轴对称图形C.对角线相等的四边形是矩形D.只要是证明两个直角三角形全等,都可以用“HL”定理9.如图,在平面直角坐标系中,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,以点
,以点![]() 为圆心,
为圆心,![]() 长为半径画弧,交
长为半径画弧,交![]() 轴的负半轴于点
轴的负半轴于点![]() ,则点
,则点![]() 的坐标为( )
的坐标为( )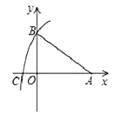 A.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 10.下列说法正确的是( )A.了解全国中学生最喜爱哪位歌手,适合全面调查.B.甲乙两种麦种,连续3年的平均亩产量相同,它们的方差为:S甲2=1,S乙2=0.1,则甲麦种产量比较稳.C.某次朗读比赛中预设半数晋级,某同学想知道自己是否晋级,除知道自己的成绩外,还需要知道平均成绩.D.一组数据:3,2,1,1,4,6的众数是1.11.一束光线从点A(3,3)出发,经过y轴上点C反射后经过点B(1,0),则光线从A点到B点经过的路线长是( )A.4 B.5 C.6 D.712.在-2,-1,0,1这四个数中,最小的数是( )A.-2 B.-1 C.0 D.1二、填空题(每题4分,满分20分,将答案填在答题纸上)13.计算
10.下列说法正确的是( )A.了解全国中学生最喜爱哪位歌手,适合全面调查.B.甲乙两种麦种,连续3年的平均亩产量相同,它们的方差为:S甲2=1,S乙2=0.1,则甲麦种产量比较稳.C.某次朗读比赛中预设半数晋级,某同学想知道自己是否晋级,除知道自己的成绩外,还需要知道平均成绩.D.一组数据:3,2,1,1,4,6的众数是1.11.一束光线从点A(3,3)出发,经过y轴上点C反射后经过点B(1,0),则光线从A点到B点经过的路线长是( )A.4 B.5 C.6 D.712.在-2,-1,0,1这四个数中,最小的数是( )A.-2 B.-1 C.0 D.1二、填空题(每题4分,满分20分,将答案填在答题纸上)13.计算![]() ______.14.约分:
______.14.约分:![]() =_________.15.函数
=_________.15.函数![]() 中,自变量x的取值范围是_____.16.如图,
中,自变量x的取值范围是_____.16.如图,![]() 是同一双曲线上的三点过这三点分别作
是同一双曲线上的三点过这三点分别作![]() 轴的垂线,垂足分别为
轴的垂线,垂足分别为![]() ,连结
,连结![]() 得到
得到![]() 的面积分别为
的面积分别为![]() .那么
.那么![]() 的大小关系为____.
的大小关系为____.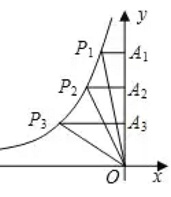 17.斜边长17cm,一条直角边长15cm的直角三角形的面积 .三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)18.(5分)如图,一次函数y=kx+b的图象分别与x轴,y轴的正半轴分別交于点A,B,AB=2
17.斜边长17cm,一条直角边长15cm的直角三角形的面积 .三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)18.(5分)如图,一次函数y=kx+b的图象分别与x轴,y轴的正半轴分別交于点A,B,AB=2![]() ,∠OAB=45°(1)求一次函数的解析式; (2)如果在第二象限内有一点C(a,
,∠OAB=45°(1)求一次函数的解析式; (2)如果在第二象限内有一点C(a,![]() );试用含有a的代数式表示四边形ABCO的面积,并求出当△ABC的面积与△ABO的面积相等时a的值; (3)在x轴上,是否存在点P,使△PAB为等腰三角形?若存在,请直接写出所有符合条件的点P坐标;若不存在,请说明理由.
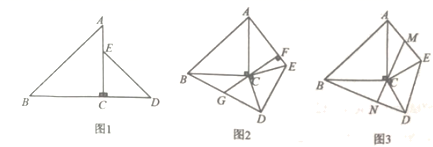
);试用含有a的代数式表示四边形ABCO的面积,并求出当△ABC的面积与△ABO的面积相等时a的值; (3)在x轴上,是否存在点P,使△PAB为等腰三角形?若存在,请直接写出所有符合条件的点P坐标;若不存在,请说明理由. 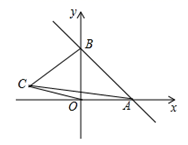 19.(5分)如图,两块大小不等的等腰直角三角形按图1放置,点
19.(5分)如图,两块大小不等的等腰直角三角形按图1放置,点![]() 为直角顶点,点
为直角顶点,点![]() 在
在![]() 上,将
上,将![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 角度
角度![]() ,连接
,连接![]() 、
、![]() .
. (1)若
(1)若![]() ,则当
,则当![]()
![]() 时,四边形
时,四边形![]() 是平行四边形;(2)图2,若
是平行四边形;(2)图2,若![]() 于点
于点![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() ,求证:
,求证:![]() 是
是![]() 的中点;(3)图3,若点
的中点;(3)图3,若点![]() 是
是![]() 的中点,连接
的中点,连接![]() 并延长交
并延长交![]() 于点
于点![]() ,求证:
,求证:![]() . 20.(8分)阅读下列材料,解决问题:学习了勾股定理后我们知道:直角三角形两条直角边的平方和等于斜边的平方.根据勾股定理我们定义:如图①,点M、N是线段AB上两点,如果线段AM、MN、NB能构成直角三角形,则称点M、N是线段AB的勾股点解决问题(1)在图①中,如果AM=2,MN=3,则NB= .(2)如图②,已知点C是线段AB上一定点(AC<BC),在线段AB上求作一点D,使得C、D是线段AB的勾股点.李玉同学是这样做的:过点C作直线GH⊥AB,在GH上截取CE=AC,连接BE,作BE的垂直平分线交AB于点D,则C、D是线段AB的勾股点你认为李玉同学的做法对吗?请说明理由(3)如图③,DE是△ABC的中位线,M、N是AB边的勾股点(AM<MN<NB),连接CM、CN分别交DE于点G、H求证:G、H是线段DE的勾股点.
. 20.(8分)阅读下列材料,解决问题:学习了勾股定理后我们知道:直角三角形两条直角边的平方和等于斜边的平方.根据勾股定理我们定义:如图①,点M、N是线段AB上两点,如果线段AM、MN、NB能构成直角三角形,则称点M、N是线段AB的勾股点解决问题(1)在图①中,如果AM=2,MN=3,则NB= .(2)如图②,已知点C是线段AB上一定点(AC<BC),在线段AB上求作一点D,使得C、D是线段AB的勾股点.李玉同学是这样做的:过点C作直线GH⊥AB,在GH上截取CE=AC,连接BE,作BE的垂直平分线交AB于点D,则C、D是线段AB的勾股点你认为李玉同学的做法对吗?请说明理由(3)如图③,DE是△ABC的中位线,M、N是AB边的勾股点(AM<MN<NB),连接CM、CN分别交DE于点G、H求证:G、H是线段DE的勾股点.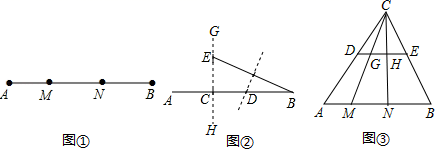 21.(10分)如图,正方形OABC的面积为4,点O为坐标原点,点B在函数y
21.(10分)如图,正方形OABC的面积为4,点O为坐标原点,点B在函数y![]() (k<0,x<0)的图象上,点P(m,n)是函数y
(k<0,x<0)的图象上,点P(m,n)是函数y![]() (k<0,x<0)的图象上异于B的任意一点,过点P分别作x轴、y轴的垂线,垂足分别为E、F.(1)设矩形OEPF的面积为S1,求S1;(1)从矩形OEPF的面积中减去其与正方形OABC重合的面积,剩余面积记为S1.写出S1与m的函数关系式,并标明m的取值范围.
(k<0,x<0)的图象上异于B的任意一点,过点P分别作x轴、y轴的垂线,垂足分别为E、F.(1)设矩形OEPF的面积为S1,求S1;(1)从矩形OEPF的面积中减去其与正方形OABC重合的面积,剩余面积记为S1.写出S1与m的函数关系式,并标明m的取值范围.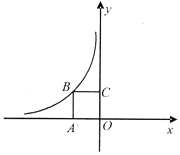 22.(10分)如图矩形ABCD中,AB=12,BC=8,E、F分别为AB、CD的中点,点P、Q从A.C同时出发,在边AD、CB上以每秒1个单位向D、B运动,运动时间为t(0<t<8).
22.(10分)如图矩形ABCD中,AB=12,BC=8,E、F分别为AB、CD的中点,点P、Q从A.C同时出发,在边AD、CB上以每秒1个单位向D、B运动,运动时间为t(0<t<8).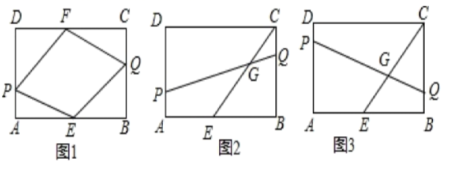 (1)如图1,连接PE、EQ、QF、PF,求证:无论t在0<t<8内取任何值,四边形PEQF总为平行四边形;(2)如图2,连接PQ交CE于G,若PG=4QG,求t的值;(3)在运动过程中,是否存在某时刻使得PQ⊥CE于G?若存在,请求出t的值:若不存在,请说明理由 23.(12分)化简求值:(1+
(1)如图1,连接PE、EQ、QF、PF,求证:无论t在0<t<8内取任何值,四边形PEQF总为平行四边形;(2)如图2,连接PQ交CE于G,若PG=4QG,求t的值;(3)在运动过程中,是否存在某时刻使得PQ⊥CE于G?若存在,请求出t的值:若不存在,请说明理由 23.(12分)化简求值:(1+![]() )÷
)÷![]() ,其中x=﹣1. 参考答案 一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.1、C2、C3、D4、B5、B6、D7、D8、A9、B10、D11、B12、A 二、填空题(每题4分,满分20分,将答案填在答题纸上)13、
,其中x=﹣1. 参考答案 一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.1、C2、C3、D4、B5、B6、D7、D8、A9、B10、D11、B12、A 二、填空题(每题4分,满分20分,将答案填在答题纸上)13、![]() 14、
14、![]() .15、x≠116、S1=S2=S117、60cm2 三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)18、(1)一次函数解析式为 y= -x+1 (1)a=−
.15、x≠116、S1=S2=S117、60cm2 三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)18、(1)一次函数解析式为 y= -x+1 (1)a=−![]() (3)存在,满足条件的点P的坐标为(0,0)或(1−1
(3)存在,满足条件的点P的坐标为(0,0)或(1−1![]() ,0)或(1
,0)或(1![]() +1,0)或(-1,0).19、(1)
+1,0)或(-1,0).19、(1)![]() 时,四边形
时,四边形![]() 是平行四边形;(2)见解析;(3)见解析.20、(1)
是平行四边形;(2)见解析;(3)见解析.20、(1)![]() 或
或![]() ;(2)对,理由见解析;(3)见解析21、(1)
;(2)对,理由见解析;(3)见解析21、(1)![]() ;(1)
;(1)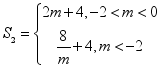 .22、(1)见解析;(2)
.22、(1)见解析;(2)![]() ;(3)不存在,理由见解析.23、
;(3)不存在,理由见解析.23、![]() ,-2.
,-2.
相关试卷
这是一份山东省威海乳山市2023-2024学年九年级数学第一学期期末检测模拟试题含答案,共8页。试卷主要包含了考生必须保证答题卡的整洁,已知函数是的图像过点,则的值为,若关于x的一元二次方程方程,下列运算正确的是,设,则代数式的值为等内容,欢迎下载使用。
这是一份山东省威海市文登区2022-2023学年七下数学期末经典模拟试题含答案,共6页。试卷主要包含了已知点P等内容,欢迎下载使用。
这是一份山东省威海市环翠区2022-2023学年七下数学期末达标测试试题含答案,共8页。试卷主要包含了已知m=,n=,则代数式的值为等内容,欢迎下载使用。









