


山东省滕州市张汪中学2022-2023学年数学七下期末监测模拟试题含答案
展开这是一份山东省滕州市张汪中学2022-2023学年数学七下期末监测模拟试题含答案,共7页。试卷主要包含了高跟鞋的奥秘,已知,则的值等于,不等式组的解集是等内容,欢迎下载使用。
山东省滕州市张汪中学2022-2023学年数学七下期末监测模拟试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
请考生注意:
1.请用2B铅笔将选择题答案涂填在答题纸相应位置上,请用0.5毫米及以上黑色字迹的钢笔或签字笔将主观题的答案写在答题纸相应的答题区内。写在试题卷、草稿纸上均无效。
2.答题前,认真阅读答题纸上的《注意事项》,按规定答题。
一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.函数![]() 中,自变量x的取值范围是( )
中,自变量x的取值范围是( )
A.x>1 B.x<1 C.![]() D.
D.![]()
2.多多班长统计去年1~8月“书香校园”活动中全班同学的课外阅读数量(单位:本),绘制了如图折线统计图,下列说法正确的是( )
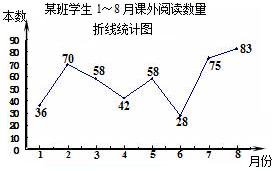
A.极差是47 B.众数是42
C.中位数是58 D.每月阅读数量超过40的有4个月
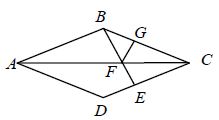
3.如图,菱形![]() 中,
中,![]() 于
于![]() ,交
,交![]() 于F,
于F,![]() 于
于![]() ,若
,若![]() 的周长为4,则菱形
的周长为4,则菱形![]() 的面积为( ).
的面积为( ).
A.![]() B.
B.![]() C.16 D.
C.16 D.![]()
4.高跟鞋的奥秘:当人肚脐以下部分的长![]() 与身高,的比值越接近0.618时,越给人以一种匀称的美感,如图,某女士身高
与身高,的比值越接近0.618时,越给人以一种匀称的美感,如图,某女士身高![]() ,脱去鞋后量得下半身长为
,脱去鞋后量得下半身长为![]() ,则建议她穿的高跟鞋高度大约为( )
,则建议她穿的高跟鞋高度大约为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.如图,在四边形ABCD中,∠A=90°,AB=3,![]() ,点M、N分别为线段BC、AB上的动点,点E、F分别为DM、MN的中点,则EF长度的最大值为( )
,点M、N分别为线段BC、AB上的动点,点E、F分别为DM、MN的中点,则EF长度的最大值为( )
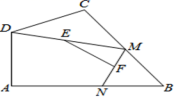
A.2 B.3 C.4 D.![]()
6.已知![]() ,则
,则![]() 的值等于( )
的值等于( )
A.6 B.-6 C.![]() D.
D.![]()
7.不等式组![]() 的解集是( )
的解集是( )
A.x>-2 B.x<1
C.-1<x<2 D.-2<x<1
8.如图,四边形ABCD为平行四边形,延长AD到E,使DE=AD,连接EB,EC,DB,下列条件中,不能使四边形DBCE成为菱形的是( )
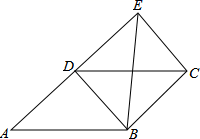
A.AB=BE B.BE⊥DC C.∠ABE=90° D.BE平分∠DBC
9.据《南昌晚报》2019 年 4 月 28 日报道,“五一”期间南昌天气预报气温如下:
时间 | 4 月 29 日 | 4 月 30 日 | 5 月 1 日 | 5 月 2 日 | 5 月 3 日 |
最低气温 | 18℃ | 18℃ | 19℃ | 18℃ | 19℃ |
最高气温 | 22℃ | 24℃ | 27℃ | 22℃ | 24℃ |
则“五一”期间南昌天气预报气温日温差最大的时间是( )
A.4 月 29 日 B.4 月 30 日 C.5 月 1 日 D.5 月 3 日
10.如图,矩形![]() 的对角线
的对角线![]() 相交于点
相交于点![]() ,
,![]() ,则
,则![]() 的周长为()
的周长为()
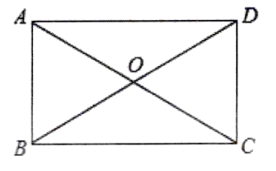
A.12 B.14 C.16 D.18
11.某种感冒病毒的直径为![]() ,用科学记数法表示为( )
,用科学记数法表示为( )
A.![]() 米 B.
米 B.![]() 米 C.
米 C.![]() 米 D.
米 D.![]() 米
米
12.如图,在矩形AOBC中,A(–2,0),B(0,1).若正比例函数y=kx的图象经过点C,则k的值为( )
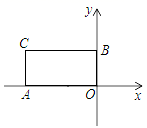
A.–![]() B.
B.![]() C.–2 D.2
C.–2 D.2
二、填空题(每题4分,满分20分,将答案填在答题纸上)
13.菱形ABCD的两条对角线长分别为6cm和8cm,则菱形ABCD的面积为_____;周长为______.
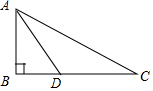
14.如图,在△ABC中,∠ABC=90°,∠ACB=30°,D是BC上的一点,且知AC=20,CD=10![]() ﹣6,则AD=_____.
﹣6,则AD=_____.
15.如图,正方形ABCD的边长为a,E是AB的中点,CF平分∠DCE,交AD于F,则AF的长为______.
16.已知点![]() ,
,![]() ,
,![]() ,在平面内找一点
,在平面内找一点![]() ,使得以
,使得以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形为平行四边形,则点
为顶点的四边形为平行四边形,则点![]() 的坐标为__________.
的坐标为__________.
17.若代数式![]() 的值大于﹣1且小于等于2,则x的取值范围是_____.
的值大于﹣1且小于等于2,则x的取值范围是_____.
三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)
18.(5分)如图所示,![]() 的顶点在
的顶点在![]() 的网格中的格点上.
的网格中的格点上.
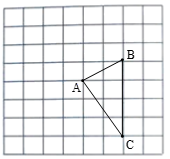
(1)画出![]() 绕点A逆时针旋转
绕点A逆时针旋转![]() 得到的
得到的![]() ;
;
(2)在图中确定格点D,并画出一个以A、B、C、D为顶点的四边形,使其为中心对称图形.
19.(5分)已知:如图所示,菱形ABCD中,E,F分别是CB,CD上的点,且BE=DF.
(1)试说明:AE=AF;
(2)若∠B=60°,点E,F分别为BC和CD的中点,试说明:△AEF为等边三角形.
20.(8分)垫球是排球队常规训练的重要项目之一.下列图表中的数据是甲、乙、丙三人每人十次垫球测试的成绩.测试规则为连续接球10个,每垫球到位1个记1分.
运动员甲测试成绩表
测试序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
成绩(分) | 7 | 6 | 8 | 7 | 7 | 5 | 8 | 7 | 8 | 7 |
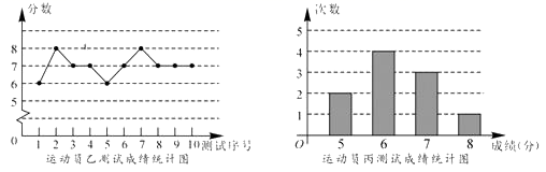
(1)写出运动员甲测试成绩的众数和中位数;
(2)在他们三人中选择一位垫球成绩优秀且较为稳定的接球能手作为自由人,你认为选谁更合适?为什么?(参考数据:三人成绩的方差分别为![]() 、
、![]() 、
、![]() )
)
21.(10分)某学校欲招聘一名新教师,对甲、乙、丙三名应试者进行了面试、笔试和才艺三个方面的量化考核,他们的各项得分(百分制)如下表所示:
应试者 | 面试成绩 | 笔试成绩 | 才艺 |
甲 | 83 | 79 | 90 |
乙 | 85 | 80 | 75 |
丙 | 80 | 90 | 73 |
(1)根据三项得分的平均分,从高到低确定应聘者的排名顺序;
(2)学校规定:笔试、面试、才艺得分分别不得低于80分、80分、70分,并按照60%、30%、10%的比例计入个人总分,请你说明谁会被录用?
22.(10分)2019年3月21日,长春市遭遇了一次大量降雪天气,市环保系统出动了多辆清雪车连夜清雪,已知一台大型清雪车比一台小型清雪车每小时多清扫路面6千米,一台大型清雪车清扫路面90千米与一台小型清雪车清扫路面60千米所用的时间相同.求一台小型清雪车每小时清扫路面的长度.
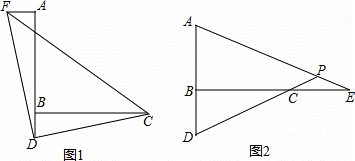
23.(12分)如图,已知∠ABC=90°,D是直线AB上的点,AD=BC.
(1)如图1,过点A作AF⊥AB,截取AF=BD,连接DC、DF、CF,判断△CDF的形状并证明;
(2)如图2,E是直线BC上一点,且CE=BD,直线AE、CD相交于点P,∠APD的度数是一个固定的值吗?若是,请求出它的度数;若不是,请说明理由.
参考答案
一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1、C
2、C
3、B
4、C
5、A
6、A
7、D
8、A
9、C
10、A
11、D
12、A
二、填空题(每题4分,满分20分,将答案填在答题纸上)
13、24 cm2 20 cm
14、1![]()
15、![]() a
a
16、![]() ,
,![]() ,
,![]()
17、﹣1≤x<1.
三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)
18、(1)见解析;(2)见解析.
19、(1)见详解;(2)见详解
20、(1)甲运动员测试成绩的众数和中位数都是7分;(2)选乙运动员更合适.
21、(1)排名顺序为:甲、丙、乙;(2)丙会被录用.
22、12千米
23、(1)△CDF是等腰三角形;(2)∠APD=45°.
相关试卷
这是一份2023-2024学年山东省滕州市张汪中学九上数学期末学业质量监测试题含答案,共7页。试卷主要包含了考生要认真填写考场号和座位序号,方程x=x的根是等内容,欢迎下载使用。
这是一份山东省滕州市张汪中学2023-2024学年数学九上期末联考试题含答案,共9页。
这是一份山东省滕州市张汪中学2023-2024学年数学八年级第一学期期末达标检测模拟试题含答案,共7页。试卷主要包含了如图,下列各式中正确的是,式子中x的取值范围是,下列实数中是无理数的是等内容,欢迎下载使用。












