山东省邹城市第六中学2022-2023学年七下数学期末经典试题含答案

这是一份山东省邹城市第六中学2022-2023学年七下数学期末经典试题含答案，共9页。试卷主要包含了下列根式是最简二次根式的是，以下命题，正确的是.等内容，欢迎下载使用。
山东省邹城市第六中学2022-2023学年七下数学期末经典试题（时间：120分钟             分数：120分） 学校_______            年级_______        姓名_______ 考生须知：1．全卷分选择题和非选择题两部分，全部在答题纸上作答。选择题必须用2B铅笔填涂；非选择题的答案必须用黑色字迹的钢笔或答字笔写在“答题纸”相应位置上。2．请用黑色字迹的钢笔或答字笔在“答题纸”上先填写姓名和准考证号。3．保持卡面清洁，不要折叠，不要弄破、弄皱，在草稿纸、试题卷上答题无效。 一、选择题(每小题3分,共30分)1．一次函数y＝﹣3x+5的图象不经过的象限是（　　）A．第一象限 B．第二象限 C．第三象限 D．第四象限2．计算的结果是（    ）A．2 B． C． D．-23．下列四幅图象近似刻画两个变量之间的关系，请按图象顺序将下面四种情景与之对应排序（ ）.①一辆汽车在公路上匀速行驶（汽车行驶的路程与时间的关系）②向锥形瓶中匀速注水（水面的高度与注水时间的关系）③将常温下的温度计插入一杯热水中（温度计的读数与时间的关系）④一杯越来越凉的水（水温与时间的关系）A．①②④③    B．③④②①C．①④②③    D．③②④①4．在▱ABCD中，对角线AC，BD交于点O，下列结论错误的是(　　)A．∠ABO＝∠CDO B．∠BAD＝∠BCDC．AB＝CD D．AC⊥BD5．如图， OABC的顶点O，A，C的坐标分别是（0，0），（2，0），（，1），则点B的坐标是（    ）A．（1，2） B．（，2） C．（，1） D．（3，1）6．如图，平行四边形ABCD的对角线AC、BD相交于点O，AE平分∠BAD，分别交BC、BD于点E、P，连接OE，∠ADC=60°，AB=BC=1，则下列结论：①∠CAD=30°②BD=③S平行四边形ABCD=AB•AC④OE=AD⑤S△APO=，正确的个数是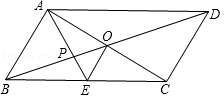（　　）A．2 B．3 C．4 D．57．下列根式是最简二次根式的是（   ）A． B． C． D．8．以下命题，正确的是（   ）.A．对角线相等的菱形是正方形B．对角线相等的平行四边形是正方形C．对角线互相垂直的平行四边形是正方形D．对角线互相垂直平分的四边形是正方形9．如图,正方形ABCD的边长为4cm,则图中阴影部分的面积为(    )cm2A．4 B．16 C．12 D．810．如图，在 ABCD中，CD=2AD，BE⊥AD于点E，F为DC的中点，连结EF、BF，下列结论：①∠ABC=2∠ABF；②EF=BF；③S四边形DEBC=2S△EFB；④∠CFE=3∠DEF,其中正确结论的个数共有（    ）.A．1个 B．2个 C．3个 D．4个二、填空题(本大题共有6小题，每小题3分，共18分)11．一组数据 ，则这组数据的方差是 __________ .12．如图，在平行四边形ABCD中，对角线AC与BD相交于点O，BD⊥AD，AD=6，AB=10，则△AOB的面积为 _________________13．如图，在平行四边形中，，．以点为圆心，适当长为半径画弧，交于点，交于点，再分别以点，为圆心，大于的长为半径画弧，两弧相交于点，射线交的延长线于点，则的长是____________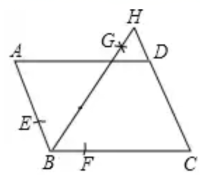．14．一组正方形按如图所示的方式放置，其中顶点在y轴上，顶点、、、、、、在x轴上，已知正方形的边长为1，，，则正方形的边长是______．15．从某市5000名初一学生中，随机地抽取100名学生，测得他们的身高数据，得到一个样本，则这个样本数据的平均数、中位数、众数、方差四个统计量中，服装厂最感兴趣的是__________.16．如图，、、、分别是四边形各边的中点，若对角线、的长都是，则四边形的周长是______.三、解下列各题(本大题共8小题，共72分)17．（8分）某校为加强学生安全意识，组织了全校1500名学生参加安全知识竞赛，从中抽取了部分学生成绩（得分取正整数，满分100分）进行统计，请根据尚为完成的频率和频数分布直方图，解答下列问题：分数段频数频率50.5～60.5160.0860.5～70.5400.270.5～80.5500.2580.5～90.5m0.3590.5～100.524n（1）这次抽取了______名学生的竞赛成绩进行统计，其中m=______，n=______；（2）补全频数分布直方图；（3）若成绩在70分以下（含70分）的学生为安全意识不强，有待进一步加强安全教育，则该校安全意识不强的学生约有多少人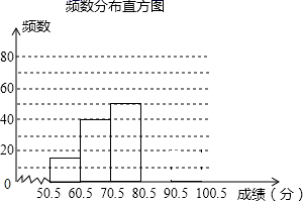？   18．（8分）（1）如图1，在矩形中，对角线与相交于点，过点作直线，且交于点，交于点，连接，且平分.①求证：四边形是菱形；②直接写出的度数；（2）把（1）中菱形进行分离研究，如图2，分别在边上，且，连接为的中点，连接，并延长交于点，连接.试探究线段与之间满足的关系，并说明理由；（3）把（1）中矩形进行特殊化探究，如图3，矩形满足时，点是对角线上一点，连接，作，垂足为点，交于点，连接，交于点.请直接写出线段三者之间满足的数量关系.   19．（8分）计算：（1）（2）已知，，求的值.   20．（8分）如图，正方形 ABCD 的边长为 8，E 是 BC 边的中点，点 P 在射线 AD 上， 过 P 作 PF⊥AE 于 F．（1）请判断△PFA 与△ABE 是否相似，并说明理由；（2）当点 P 在射线 AD 上运动时，设 PA＝x，是否存在实数 x，使以 P，F，E 为顶 点的三角形也与△ABE 相似？若存在，请求出 x 的值；若不存在，说明理由．   21．（8分）为发展旅游经济，我市某景区对门票釆用灵活的售票方法吸引游客．门票定价为50元/人，非节假日打折售票，节假日按团队人数分段定价售票，即人以下（含人）的团队按原价售票；超过人的团队，其中人仍按原价售票，超过人部分的游客打折售票．设某旅游团人数为人，非节假日购票款为（元），节假日购票款为（元）．与之间的函数图象如图所示．（1）观察图象可知：　   　；　   　；　   　；（2）直接写出，与之间的函数关系式；（3）某旅行社导游王娜于5月1日带团，5月20日（非节假日）带团都到该景区旅游，共付门票款1900元，，两个团队合计50人，求，两个团队各有多少人？   22．（10分）如图，在△ABC中，∠ABC=90°，BD为AC边上的中线．（1）按如下要求尺规作图，保留作图痕迹，标注相应的字母：过点C作直线CE，使CE⊥BC于点C，交BD的延长线于点E，连接AE；（2）求证：四边形ABCE是矩形．   23．（10分）如图，抛物线y＝ax2+bx﹣3过A（1，0），B（﹣3，0），直线AD交抛物线于点D，点D的横坐标为﹣2，点P（m，n）是线段AD上的动点．（1）求直线AD及抛物线的解析式；（2）过点P的直线垂直于x轴，交抛物线于点Q，求线段PQ的长度l与m的关系式，m为何值时，PQ最长？（3）在平面内是否存在整点（横、纵坐标都为整数）R，使得P，Q，D，R为顶点的四边形是平行四边形？若存在，直接写出点R的坐标；若不存在，说明理由．   24．（12分）如图，在直角坐标系中，已知点O，A的坐标分别为（0，0），（﹣3，﹣2）．（1）点B的坐标是　   　，点B与点A的位置关系是　   　．现将点B，点A都向右平移5个单位长度分别得到对应点C和D，顺次连接点A，B，C，D，画出四边形ABCD；（2）横、纵坐标都是整数的点成为整数点，在四边形ABCD内部（不包括边界）的整数点M使S△ABM＝8，请直接写出所有点M的可能坐标；（3）若一条经过点（0，﹣4）的直线把四边形ABCD的面积等分，则这条直线的表达式是　   　，并在图中画出这条直线．   参考答案 一、选择题(每小题3分,共30分)1、C2、A3、D4、D5、C6、D7、C8、A9、D10、D 二、填空题(本大题共有6小题，每小题3分，共18分)11、112、1213、314、  15、众数16、 三、解下列各题(本大题共8小题，共72分)17、（1）200，70，0.12；（2）详见解析；（3）42018、 (1)①见解析;②60°;(1)见解析;(3)见解析.19、（1）；（2）8.20、（1）见解析；（2）存在，x的值为2或5.21、（1），，；（2），；（3）团有40人，团有10人22、 (1)见解析;(2)见解析.23、（1）y＝x2+2x﹣1；（2）当m＝-时，PQ最长，最大值为；（1）R1（﹣2，﹣2），R2（﹣2，﹣4），R1（﹣2，﹣1），R4（﹣2，﹣5），R5（0，﹣1）．24、（1）（﹣3，2），关于x轴对称；（2）点M（1，1），（1，0），（1，﹣1）；（3）y＝﹣8x﹣1