山东省龙口市兰高镇兰高校2022-2023学年七下数学期末经典试题含答案

这是一份山东省龙口市兰高镇兰高校2022-2023学年七下数学期末经典试题含答案，共8页。
山东省龙口市兰高镇兰高校2022-2023学年七下数学期末经典试题（时间：120分钟             分数：120分） 学校_______            年级_______        姓名_______ 考生须知：1．全卷分选择题和非选择题两部分，全部在答题纸上作答。选择题必须用2B铅笔填涂；非选择题的答案必须用黑色字迹的钢笔或答字笔写在“答题纸”相应位置上。2．请用黑色字迹的钢笔或答字笔在“答题纸”上先填写姓名和准考证号。3．保持卡面清洁，不要折叠，不要弄破、弄皱，在草稿纸、试题卷上答题无效。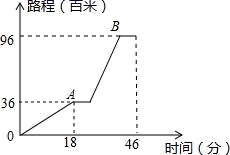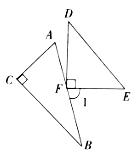 一、选择题(每小题3分,共30分)1．下列式子：①；②；③；④.其中是的函数的个数是（    ）A．1 B．2 C．3 D．42．巫溪某中学组织初一初二学生举行“四城同创”宣传活动，从学校坐车出发，先上坡到达A地后，宣传8分钟；然后下坡到B地宣传8分钟返回，行程情况如图．若返回时，上、下坡速度仍保持不变，在A地仍要宣传8分钟，那么他们从B地返回学校用的时间是(   )A．45.2分钟 B．48分钟 C．46分钟 D．33分钟3．只用下列图形不．能．进行平面镶嵌的是（    ）A．全等的三角形 B．全等的四边形C．全等的正五边形 D．全等的正六边形4．将一幅三角板如图所示摆放，若，那么∠1的度数为（）（提示：延长EF或DF）A．45° B．60° C．75° D．80°5．下列四组线段中，可以构成直角三角形的是（    ）A．2、3、4 B．、2、 C．3、4、5 D．5、6、76．学校测量了全校800名男生的身高，并进行了分组，已知身高在1.70~1.75（单位：m）这一组的频率为0.25，则该组共有男生（      ）A．100名 B．200名 C．250名 D．400名7．已知平行四边形中，一个内角，那么它的邻角（    ）.A． B． C． D．8．如图，在Rt△ABC中，AC＝4，∠ABC＝90°，BD是△ABC的角平分线，过点D作DE⊥BD交BC边于点E．若AD＝1，则图中阴影部分面积为(　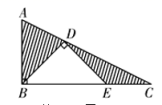  )A．1 B．1.5 C．2 D．2.59．已知关于x的一元二次方程2x2﹣mx﹣4=0的一个根为m，则m的值是（　　）A．2 B．﹣2 C．2或﹣2 D．任意实数10．如图，正方形的边长是4，在上，且，是边上的一动点，则周长的最小值是( 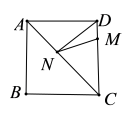   )A．3 B．4 C．5 D．6二、填空题(本大题共有6小题，每小题3分，共18分)11．如图，在中，，交于点，，若，则__________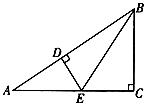．12．数据2，0，1，9，0，6，1，6的中位数是______．13．已知一次函数的图象经过第一、二、四象限，则的取值范围是_____．14．一次函数图象过点日与直线平行，则一次函数解析式__________．15．在平面直角坐标系中，已知坐标，将线段(第一象限)绕点(坐标原点)按逆时针方向旋转后，得到线段，则点的坐标为____．16．如图，在中，，，，过点作且点在点的右侧．点从点出发沿射线方向以/秒的速度运动，同时点从点出发沿射线方向以/秒的速度运动，在线段上取点，使得，设点的运动时间为秒．当__________秒时，以，，，为顶点的四边形是平行四边形．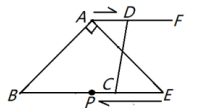三、解下列各题(本大题共8小题，共72分)17．（8分）已知：如图，在矩形ABCD中，M，N分别是边AD、BC的中点，E，F分别是线段BM，CM的中点．（1）求证：BM＝CM；（2）判断四边形MENF是什么特殊四边形，并证明你的结论；（3）当矩形ABCD的长和宽满足什么条件时，四边形MENF是正方形？为什么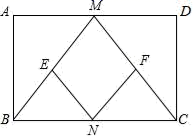？   18．（8分）阅读可以增进人们的知识，也能陶冶人们的情操．我们要多阅读有营养的书．某校对学生的课外阅读时间进行了抽样调查，将收集的数据分成A，B，C，D，E五组进行整理，并绘制成如图所示的统计图表(图中信息不完整)．阅读时间分组统计表组别阅读时间x(h)人数A0≤x＜10aB10≤x＜20100C20≤x＜30bD30≤x＜40140Ex≥40c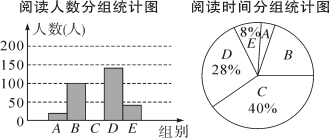请结合以上信息解答下列问题：(1)求a，b，c的值；(2)补全“阅读人数分组统计图”；(3)估计全校课外阅读时间在20h以下(不含20h)的学生所占百分比．   19．（8分）如图，在平面直角坐标系中，为坐标原点，矩形的顶点、，将矩形的一个角沿直线折叠，使得点落在对角线上的点处，折痕与轴交于点．   （1）求线段的长度；   （2）求直线所对应的函数表达式；   （3）若点在线段上，在线段上是否存在点，使以为顶点的四边形是平行四边形？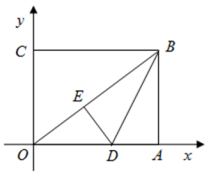若存在，请求出点的坐标；若不存在，请说明理由．   20．（8分）如图，已知点A的坐标为（a，4）（其中a<-3），射线OA与反比例函数的图象交于点P，点B，C分别在函数的图象上，且AB∥x轴，AC∥y轴，连结BO，CO，BP，CP．（1）当a=-6，求线段AC的长；（2）当AB=BO时，求点A的坐标；（3）求证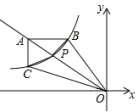：．   21．（8分）已知点E、F分别是四边形ABCD边AB、AD上的点，且DE与CF相交于点G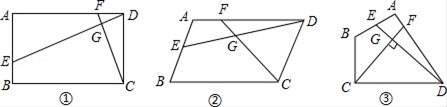．（1）如图①，若AB∥CD，AB＝CD，∠A＝90°，且AD•DF＝AE•DC，求证：DE⊥CF：（2）如图②，若AB∥CD，AB＝CD，且∠A＝∠EGC时，求证：DE•CD＝CF•DA：（3）如图③，若BA＝BC＝3，DA＝DC＝4，设DE⊥CF，当∠BAD＝90°时，试判断是否为定值，并证明．   22．（10分）先化简，再求值：+（x﹣2）2﹣6，其中，x=+1．   23．（10分）某商贩出售一批进价为l元的钥匙扣，在销售过程中发现钥匙扣的日销售单价x（元）与日销售量y（个）之间有如下关系：（1）根据表中数据在平面直角坐标系中，描出实数对（x，y）对应的点；（2）猜想并确定y与x的关系式，并在直角坐标系中画出x>0时的图像；（3）设销售钥匙扣的利润为T元，试求出T与x之间的函数关系式：若商贩在钥匙扣售价不超过8元的前提下要获得最大利润，试求销售价x和最大利润T．   24．（12分）已知：关于x的一元二次方程ax2﹣2（a﹣1）x+a﹣2=0（a＞0）．（1）求证：方程有两个不相等的实数根；（2）设方程的两个实数根分别为x1，x2（其中x1＞x2）．若y是关于a的函数，且y=ax2•x1，求这个函数的表达式；（3）将（2）中所得的函数的图象在直线a=2的左侧部分沿直线a=2翻折，图象的其余部分保持不变，得到一个新的图象．请你结合这个新的图象直接写出：当关于a的函数y=2a+b的图象与此图象有两个公共点时，b的取值范围是　　．   参考答案 一、选择题(每小题3分,共30分)1、C2、A3、C4、C5、C6、B7、C8、B9、C10、D 二、填空题(本大题共有6小题，每小题3分，共18分)11、112、1.213、14、15、16、或14 三、解下列各题(本大题共8小题，共72分)17、 (1)见解析；（2）平行四边形MENF是菱形,见解析；（3）即当AD：AB＝2：1时，四边形MENF是正方形,理由见解析.18、 (1)20，200，40；(2)补全图形见解析；(3) 24%.19、（1）15；（2）；（3）20、（1）；（2）；（3）见解析21、（1）证明见解析  （2）证明见解析  （3）答案见解析22、（x﹣1）2+3；8.23、（1）见解析；（2），见解析；（3），，（元）.24、（1）见解析；（2）y=a﹣1（a＞0）；（1）﹣11＜b＜﹣2