


山西省晋中学市榆社县2022-2023学年数学七年级第二学期期末统考模拟试题含答案
展开这是一份山西省晋中学市榆社县2022-2023学年数学七年级第二学期期末统考模拟试题含答案,共6页。试卷主要包含了考生要认真填写考场号和座位序号,若,则下列不等式正确的是,计算的结果是,下列各点中,在第四象限的点是等内容,欢迎下载使用。
山西省晋中学市榆社县2022-2023学年数学七年级第二学期期末统考模拟试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
注意事项
1.考生要认真填写考场号和座位序号。
2.试题所有答案必须填涂或书写在答题卡上,在试卷上作答无效。第一部分必须用2B 铅笔作答;第二部分必须用黑色字迹的签字笔作答。
3.考试结束后,考生须将试卷和答题卡放在桌面上,待监考员收回。
一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.一个不透明的盒子中装有2个红球和1个白球,它们除颜色外都相同.若从中任意摸出一个球,则下列叙述正确的是( )
A.摸到红球是必然事件
B.摸到白球是不可能事件
C.摸到红球与摸到白球的可能性相等
D.摸到红球比摸到白球的可能性大
2.当![]() 时,函数
时,函数![]() 的值是( )
的值是( )
A.-3 B.-5 C.-7 D.-9
3.某校要从四名学生中选拔一名参加市“风华小主播”大赛,选拔赛中每名学生的平均成绩![]() 及其方差
及其方差![]() 如表所示.如果要选择一名成绩高且发挥稳定的学生参赛,则应选择的学生是( )
如表所示.如果要选择一名成绩高且发挥稳定的学生参赛,则应选择的学生是( )
| 甲 | 乙 | 丙 | 丁 | |
| 8 | 9 | 9 | 8 | |
| 1 | 1 | 1.2 | 1.3 |
A.甲 B.乙 C.丙 D.丁
4.若![]() ,则下列不等式正确的是
,则下列不等式正确的是![]()
![]()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.计算![]() 的结果是( )
的结果是( )
A.4 B.±![]() C.2 D.
C.2 D.![]()
6.共享单车为市民出行带来了方便,某单车公司第一个月投放1000辆单车,计划第三个月投放单车数量比第一个月多440辆.设该公司第二、三两个月投放单车数量的月平均增长率为x,则所列方程正确的为( )
A.1000(1+x)2=1000+440 B.1000(1+x)2=440
C.440(1+x)2=1000 D.1000(1+2x)=1000+440
7.下表记录了四名运动员参加男子跳高选拔赛成绩的平均数![]() 与方差
与方差![]() :
:
| 甲 | 乙 | 丙 | 丁 |
平均数 | 173 | 175 | 175 | 174 |
方差 | 3.5 | 3.5 | 12.5 | 15 |
如果选一名运动员参加比赛,应选择( )
A.甲 B.乙 C.丙 D.丁
8.若关于x的分式方程![]() =1的解为正数,则m的取值范围是( )
=1的解为正数,则m的取值范围是( )
A.m>3 B.m≠-2 C.m>-3且m≠1 D.m>-3且m≠-2
9.下列各点中,在第四象限的点是( )
A.(2,3) B.(﹣2,﹣3) C.(2,﹣3) D.(﹣2,3)
10.为了响应“绿水青山就是金山银山”的号召,建设生态文明,某工厂自2019年1月开始限产并进行治污改造,其月利润![]() (万元)与月份
(万元)与月份![]() 之间的变化如图所示,治污完成前是反比例函数图象的一部分,治污完成后是一次函数图象的部分,下列选项错误的是( )
之间的变化如图所示,治污完成前是反比例函数图象的一部分,治污完成后是一次函数图象的部分,下列选项错误的是( )
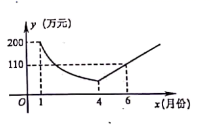
A.4月份的利润为![]() 万元
万元
B.污改造完成后每月利润比前一个月增加![]() 万元
万元
C.治污改造完成前后共有![]() 个月的利润低于
个月的利润低于![]() 万元
万元
D.9月份该厂利润达到![]() 万元
万元
11.一个事件的概率不可能是( )
A.1 B.0 C.![]() D.
D.![]()
12.下面哪个点在函数![]() 的图象上( )
的图象上( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
二、填空题(每题4分,满分20分,将答案填在答题纸上)
13.不等式组![]() 的解集是________
的解集是________
14.某水池容积为300m3,原有水100m3,现以xm3/min的速度匀速向水池中注水,注满水需要ymin,则y关于x的函数表达式为________.
15.若直角三角形的两直角边长为a、b,且满足![]() ,则该直角三角形的斜边长为 .
,则该直角三角形的斜边长为 .
16.当k取_____时,100x2﹣kxy+4y2是一个完全平方式.
17.某小区20户家庭的日用电量(单位:千瓦时)统计如下:
![]()
这20户家庭日用电量的众数、中位数分别是( )
A.6,6.5 B.6,7 C.6,7.5 D.7,7.5
三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)
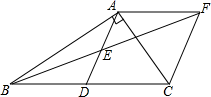
18.(5分)在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线于点F,连接CF.
(1)求证:AF=BD.
(2)求证:四边形ADCF是菱形.
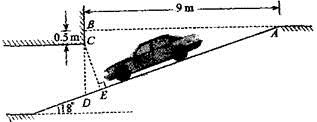
19.(5分)为缓解“停车难”问题,某单位拟建造地下停车库,建筑设计师提供了该地下停车库的设计示意图.按规定,地下停车库坡道口上方要张贴限高标志,以便告知停车人车辆能否安全驶入.(其中AB=9m,BC=0.5m)为标明限高,请你根据该图计算CE.(精确到0.1m)(参考数值![]() ,
,![]() ,
,![]() )
)
20.(8分)某家电销售商城电冰箱的销售价为每台2100元,空调的销售价为每台1750元,每台电冰箱的进价比每台空调的进价多400元,商城用80000元购进电冰箱的数量与用64000元购进空调的数量相等.
(1)求每台电冰箱与空调的进价分别是多少?
(2)现在商城准备一次购进这两种家电共100台,设购进电冰箱![]() 台,这100台家电的销售总利润为
台,这100台家电的销售总利润为![]() 元,要求购进空调数量不超过电冰箱数量的2倍,试确定获利最大的方案以及最大利润.
元,要求购进空调数量不超过电冰箱数量的2倍,试确定获利最大的方案以及最大利润.
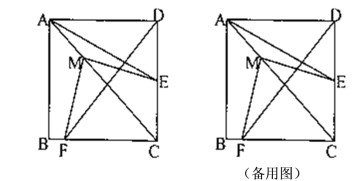
21.(10分)在正方形![]() 中,点
中,点![]() 是边
是边![]() 的中点,点
的中点,点![]() 是对角线
是对角线![]() 上的动点,连接
上的动点,连接![]() ,过点
,过点![]() 作
作![]() 交正方形的边于点
交正方形的边于点![]() ;
;
(1)当点![]() 在边
在边![]() 上时,①判断
上时,①判断![]() 与
与![]() 的数量关系;
的数量关系;
②当![]() 时,判断点
时,判断点![]() 的位置;
的位置;
(2)若正方形的边长为2,请直接写出点![]() 在
在![]() 边上时,
边上时,![]() 的取值范围.
的取值范围.
22.(10分)在校园手工制作活动中,现有甲、乙两人接到手工制作纸花任务,已知甲每小时制作纸花比乙每小时制作纸花少20朵,甲制作120朵纸花的时间与乙制作160朵纸花的时间相同,求乙每小时制作多少朵纸花?
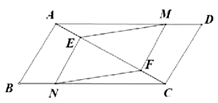
23.(12分)如图,在![]() 中,点
中,点![]() 分别在
分别在![]() 上,点
上,点![]() 在对角线
在对角线![]() 上,且
上,且![]() .求证:四边形
.求证:四边形![]() 是平行四边形.
是平行四边形.
参考答案
一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1、D
2、C
3、B
4、C
5、C
6、A
7、B
8、D
9、C
10、C
11、D
12、B
二、填空题(每题4分,满分20分,将答案填在答题纸上)
13、x 1
14、y=![]()
15、1.
16、±40
17、A
三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)
18、(1)见解析;(2)见解析.
19、2.3m
20、(1)每台空调进价为1600元,电冰箱进价为2000元;(2)当购进电冰箱34台,空调66台获利最大,最大利润为13300元.
21、(1)①![]() ,理由详见解析;②点
,理由详见解析;②点![]() 位于正方形两条对角线的交点处(或
位于正方形两条对角线的交点处(或![]() 中点出),理由详见解析;(2)
中点出),理由详见解析;(2)![]()
22、乙每小时制作80朵纸花.
23、证明见解析.
相关试卷
这是一份山西省晋中学市榆社县2023-2024学年八上数学期末调研试题含答案,共7页。试卷主要包含了考生要认真填写考场号和座位序号,已知,则a+b+c的值是,点M等内容,欢迎下载使用。
这是一份山西省晋中学市榆社县2023-2024学年数学八年级第一学期期末监测模拟试题含答案,共7页。试卷主要包含了下列图形中,为轴对称图形的是等内容,欢迎下载使用。
这是一份江苏省苏州市吴中学区统考2022-2023学年七年级数学第二学期期末统考模拟试题含答案,共7页。试卷主要包含了在中,,则的长为等内容,欢迎下载使用。












