


山西省太原市杏花岭区育英中学2022-2023学年七下数学期末经典模拟试题含答案
展开
这是一份山西省太原市杏花岭区育英中学2022-2023学年七下数学期末经典模拟试题含答案,共7页。试卷主要包含了下列图形中,第条线段组成.,一元二次方程的根是等内容,欢迎下载使用。
山西省太原市杏花岭区育英中学2022-2023学年七下数学期末经典模拟试题(时间:120分钟 分数:120分) 学校_______ 年级_______ 姓名_______ 考生须知:1.全卷分选择题和非选择题两部分,全部在答题纸上作答。选择题必须用2B铅笔填涂;非选择题的答案必须用黑色字迹的钢笔或答字笔写在“答题纸”相应位置上。2.请用黑色字迹的钢笔或答字笔在“答题纸”上先填写姓名和准考证号。3.保持卡面清洁,不要折叠,不要弄破、弄皱,在草稿纸、试题卷上答题无效。 一、选择题(每小题3分,共30分)1.如图,在平行四边形![]() 中,
中,![]() 于点E,以点B为中心,取旋转角等于
于点E,以点B为中心,取旋转角等于![]() ,将
,将![]() 顺时针旋转,得到
顺时针旋转,得到![]() .连接
.连接![]() ,若
,若![]() ,
,![]() ,则
,则![]() 的度数为( )
的度数为( )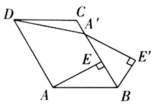 A.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 2.如图,菱形ABCD的对角线AC、BD的长分别为6和8,则这个菱形的面积是( )
2.如图,菱形ABCD的对角线AC、BD的长分别为6和8,则这个菱形的面积是( )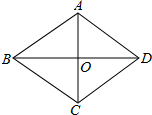 A.24 B.30 C.40 D.483.如图,
A.24 B.30 C.40 D.483.如图, ![]() ,
,![]() ,垂足分别是
,垂足分别是![]() ,
,![]() ,且
,且![]() ,若利用“
,若利用“![]() ”证明
”证明![]() ,则需添加的条件是( )
,则需添加的条件是( ) 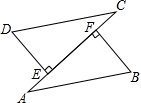 A.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 4.已知一次函数y1=2x+m与y2=2x+n(m≠n)的图象如图所示,则关于x与y的二元一次方程组
4.已知一次函数y1=2x+m与y2=2x+n(m≠n)的图象如图所示,则关于x与y的二元一次方程组 ![]() 的解的个数为( )
的解的个数为( )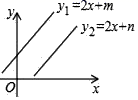 A.0个 B.1个 C.2个 D.无数个5.下列图形中,第(1)个图形由4条线段组成,第(2)个图形由10条线段组成,第(3)个图形由18条线段组成,…………第(6)个图形由( )条线段组成.
A.0个 B.1个 C.2个 D.无数个5.下列图形中,第(1)个图形由4条线段组成,第(2)个图形由10条线段组成,第(3)个图形由18条线段组成,…………第(6)个图形由( )条线段组成. A.24 B.34 C.44 D.546.下列函数中,y随x的增大而减小的函数是( )A.
A.24 B.34 C.44 D.546.下列函数中,y随x的增大而减小的函数是( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 7.如图,∠BAC=90°,四边形ADEB、BFGC、CHIA均为正方形,若 S四边形ADEB=6,S四边形BFGC=18,四边形CHIA的周长为( )
7.如图,∠BAC=90°,四边形ADEB、BFGC、CHIA均为正方形,若 S四边形ADEB=6,S四边形BFGC=18,四边形CHIA的周长为( )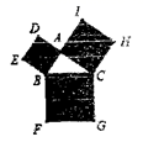 A.4
A.4![]() B.8
B.8![]() C.12
C.12![]() D.8
D.8![]() 8.如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=3,H是AF的中点,那么CH的长是( )
8.如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=3,H是AF的中点,那么CH的长是( )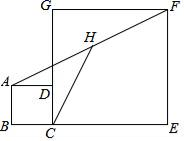 A.
A.![]() B.
B.![]() C.
C.![]() D.29.一元二次方程
D.29.一元二次方程![]() 的根是( )A.
的根是( )A.![]() B.
B.![]() C.
C.![]() ,
,![]() D.无实数根10.如图,矩形ABCD边AD沿折痕AE折叠,使点D落在BC上的F处,已知AB=6,△ABF的面积是24,则FC等于( )
D.无实数根10.如图,矩形ABCD边AD沿折痕AE折叠,使点D落在BC上的F处,已知AB=6,△ABF的面积是24,则FC等于( )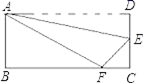 A.1 B.2 C.3 D.4二、填空题(本大题共有6小题,每小题3分,共18分)11.如图,正方形ABCD的边长为4,P为对角线AC上一点,且CP = 3
A.1 B.2 C.3 D.4二、填空题(本大题共有6小题,每小题3分,共18分)11.如图,正方形ABCD的边长为4,P为对角线AC上一点,且CP = 3![]() ,PE⊥PB交CD于点E,则PE =____________.
,PE⊥PB交CD于点E,则PE =____________.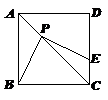 12.某老师为了了解学生周末利用网络进行学习的时间,在所任教班级随机调查了10名学生,其统计数据如下表:时间(单位:小时)
12.某老师为了了解学生周末利用网络进行学习的时间,在所任教班级随机调查了10名学生,其统计数据如下表:时间(单位:小时)
4
3
2
1
0
人数
2
4
2
1
1
则这10名学生周末利用网络进行学均时间是 小时.13.已知![]() 的对角线
的对角线![]() ,
,![]() 相交于点
相交于点![]() ,
,![]() 是等边三角形,且
是等边三角形,且![]() ,则
,则![]() 的长为__________.14.如图,菱形ABCD的对角线相交于点O,若AB=5,OA=4,则菱形ABCD的面积_____.
的长为__________.14.如图,菱形ABCD的对角线相交于点O,若AB=5,OA=4,则菱形ABCD的面积_____.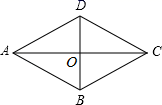 15.如图,四边形ABCD中,AB∥CD,要使四边形ABCD为平行四边形,则可添加的条件为_______________________________.(填一个即可)
15.如图,四边形ABCD中,AB∥CD,要使四边形ABCD为平行四边形,则可添加的条件为_______________________________.(填一个即可)  16.如图,菱形ABCD中,对角线AC、BD相交于点O,且AC=24,BD=10,若点E是BC边的中点,则OE的长是_____.
16.如图,菱形ABCD中,对角线AC、BD相交于点O,且AC=24,BD=10,若点E是BC边的中点,则OE的长是_____.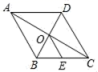 三、解下列各题(本大题共8小题,共72分)17.(8分)如图,在
三、解下列各题(本大题共8小题,共72分)17.(8分)如图,在![]() ABC中,∠C=90º,BD是
ABC中,∠C=90º,BD是![]() ABC的一条角一平分线,点O、E、F分别在BD、BC、AC上,且四边形OECF是正方形,
ABC的一条角一平分线,点O、E、F分别在BD、BC、AC上,且四边形OECF是正方形,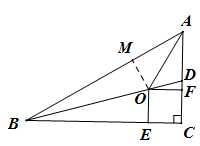 (1)求证:点O在∠BAC的平分线上;(2)若AC=5,BC=12,求OE的长 18.(8分)如图,在△ABC中,AB=AC,D是BA延长线上的一点,点E是AC的中点.
(1)求证:点O在∠BAC的平分线上;(2)若AC=5,BC=12,求OE的长 18.(8分)如图,在△ABC中,AB=AC,D是BA延长线上的一点,点E是AC的中点.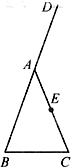 (1)实践与操作:利用尺规按下列要求作图,并在图中标明相应字母(保留作图痕迹,不写作法).①作∠DAC的平分线AM;②连接BE并延长交AM于点F;③连接FC.(2)猜想与证明:猜想四边形ABCF的形状,并说明理由. 19.(8分)贵成高铁开通后极大地方便了人们的出行,甲、乙两个城市相距450千米,加开高铁列车后,高铁列车行驶时间比原特快列车行驶时间缩短了3小时,已知高铁列车平均行驶速度是原特快列车平均行驶速度的3倍,求高铁列车的平均行驶速度. 20.(8分) (1)分解因式:﹣m+2m2﹣m3(2)化简:(
(1)实践与操作:利用尺规按下列要求作图,并在图中标明相应字母(保留作图痕迹,不写作法).①作∠DAC的平分线AM;②连接BE并延长交AM于点F;③连接FC.(2)猜想与证明:猜想四边形ABCF的形状,并说明理由. 19.(8分)贵成高铁开通后极大地方便了人们的出行,甲、乙两个城市相距450千米,加开高铁列车后,高铁列车行驶时间比原特快列车行驶时间缩短了3小时,已知高铁列车平均行驶速度是原特快列车平均行驶速度的3倍,求高铁列车的平均行驶速度. 20.(8分) (1)分解因式:﹣m+2m2﹣m3(2)化简:(![]() +
+![]() )÷(
)÷(![]() ﹣
﹣![]() ). 21.(8分)解不等式组:
). 21.(8分)解不等式组: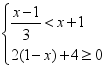 ,并在数轴上表示出它的解集。
,并在数轴上表示出它的解集。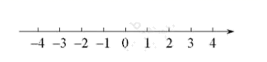 22.(10分)根据下列条件分别确定函数y=kx+b的解析式:(1)y与x成正比例,当x=5时,y=6;(2)直线y=kx+b经过点(3,6)与点(2,-4). 23.(10分)某公司需招聘一名员工,对应聘者甲、乙、丙从笔试、面试、体能三个方面进行量化考核.甲、乙、丙各项得分如下表: 笔 试面 试体 能甲858075乙809073丙837990(1)根据三项得分的平均分,从高到低确定三名应聘者的排名顺序.(2)该公司规定:笔试,面试、体能得分分别不得低于80分,80分,70分,并按60%,30%,10%的比例计入总分(不计其他因素条件),请你说明谁将被录用. 24.(12分)图①,图②都是由一个正方形和一个等腰直角三角形组成的图形.
22.(10分)根据下列条件分别确定函数y=kx+b的解析式:(1)y与x成正比例,当x=5时,y=6;(2)直线y=kx+b经过点(3,6)与点(2,-4). 23.(10分)某公司需招聘一名员工,对应聘者甲、乙、丙从笔试、面试、体能三个方面进行量化考核.甲、乙、丙各项得分如下表: 笔 试面 试体 能甲858075乙809073丙837990(1)根据三项得分的平均分,从高到低确定三名应聘者的排名顺序.(2)该公司规定:笔试,面试、体能得分分别不得低于80分,80分,70分,并按60%,30%,10%的比例计入总分(不计其他因素条件),请你说明谁将被录用. 24.(12分)图①,图②都是由一个正方形和一个等腰直角三角形组成的图形.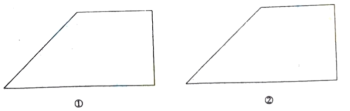 (1)用实线把图①分割成六个全等图形;(2)用实线把图②分割成四个全等图形. 参考答案 一、选择题(每小题3分,共30分)1、D2、A3、B4、A5、D6、C7、B8、A9、C10、B 二、填空题(本大题共有6小题,每小题3分,共18分)11、
(1)用实线把图①分割成六个全等图形;(2)用实线把图②分割成四个全等图形. 参考答案 一、选择题(每小题3分,共30分)1、D2、A3、B4、A5、D6、C7、B8、A9、C10、B 二、填空题(本大题共有6小题,每小题3分,共18分)11、![]() 12、2.5小时13、
12、2.5小时13、![]() .14、315、AD∥BC(答案不唯一)16、6.1. 三、解下列各题(本大题共8小题,共72分)17、(1)证明见解析;(2)2.18、(1)详见解析;(2)四边形ABCF是平行四边形.19、高铁列车平均速度为300km/h.20、解:(1)﹣m(1﹣m)2;(2)
.14、315、AD∥BC(答案不唯一)16、6.1. 三、解下列各题(本大题共8小题,共72分)17、(1)证明见解析;(2)2.18、(1)详见解析;(2)四边形ABCF是平行四边形.19、高铁列车平均速度为300km/h.20、解:(1)﹣m(1﹣m)2;(2)![]() .21、-2<x≤3,数轴上表示见解析.22、(1)
.21、-2<x≤3,数轴上表示见解析.22、(1)![]() ;(2)
;(2)![]() .23、(1)丙,乙,甲;(2)甲被录用.24、 (1)见解析;(2)见解析.
.23、(1)丙,乙,甲;(2)甲被录用.24、 (1)见解析;(2)见解析.
相关试卷
这是一份2023-2024学年山西省太原市杏花岭区育英中学数学九年级第一学期期末质量跟踪监视模拟试题含答案,共8页。试卷主要包含了下列事件中,是必然事件的是等内容,欢迎下载使用。
这是一份2023-2024学年山西省太原市杏花岭区育英中学数学八上期末质量跟踪监视试题含答案,共8页。试卷主要包含了下列各点中,位于第二象限的是,数字用科学记数法表示为等内容,欢迎下载使用。
这是一份2023-2024学年山西省太原市育英中学数学八上期末经典试题含答案,共7页。








