


广东省宝塔实验2022-2023学年七下数学期末检测模拟试题含答案
展开广东省宝塔实验2022-2023学年七下数学期末检测模拟试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
请考生注意:
1.请用2B铅笔将选择题答案涂填在答题纸相应位置上,请用0.5毫米及以上黑色字迹的钢笔或签字笔将主观题的答案写在答题纸相应的答题区内。写在试题卷、草稿纸上均无效。
2.答题前,认真阅读答题纸上的《注意事项》,按规定答题。
一、选择题(每小题3分,共30分)
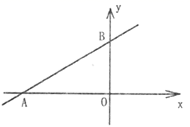
1.如图,直线![]() 交坐标轴于
交坐标轴于![]() 、
、![]() 两点,则不等式
两点,则不等式![]() 的解集为( )
的解集为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2. “古诗•送郎从军:送郎一路雨飞池,十里江亭折柳枝;离人远影疾行去,归来梦醒度相思.”中,如果用纵轴y表示从军者与送别者行进中离原地的距离,用横轴x表示送别进行的时间,从军者的图象为O→A→B→C,送别者的图象为O→A→B→D,那么下面的图象与上述诗的含义大致吻合的是( )
A.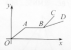 B.
B.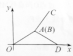 C.
C.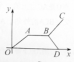 D.
D.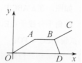
3.下列所给图形中,既是中心对称图形又是轴对称图形的是( )
A. B.
B. C.
C. D.
D.
4.9的算术平方根是( )
A.﹣3 B.±3 C.3 D.![]()
5.在平面直角坐标系中,点P(﹣3,2)关于x轴的对称点的坐标为( )
A.(2,﹣3) B.(﹣2,3) C.(﹣3,2) D.(﹣3,﹣2)
6.一元二次方程 x2= x的根是( )
A.![]() =0,
=0,![]() =1 B.
=1 B.![]() =0,
=0,![]() =-1 C.
=-1 C.![]() =
=![]() =0 D.
=0 D.![]() =
=![]() =1
=1
7.如图,点![]() 是矩形
是矩形![]() 的对角线
的对角线![]() 的中点,点
的中点,点![]() 是
是![]() 边的中点,若
边的中点,若![]() ,
,![]() ,则
,则![]() 的长为()
的长为()
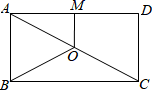
A.3 B.4 C.4.5 D.5
8.如图,矩形ABCD中,对角线AC,BD相交于点O,下列结论不一定成立的是![]()
![]()
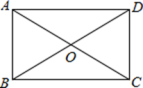
A.![]()
B.![]()
C.![]()
D.![]()
9.某农科所对甲、乙两种小麦各选用10块面积相同的试验田进行种植试验,它们的平均亩产量分别是![]() =610千克,
=610千克,![]() =608千克,亩产量的方差分别是
=608千克,亩产量的方差分别是![]() ="29." 6,
="29." 6,![]() ="2." 7. 则关于两种小麦推广种植的合理决策是 ( )
="2." 7. 则关于两种小麦推广种植的合理决策是 ( )
A.甲的平均亩产量较高,应推广甲
B.甲、乙的平均亩产量相差不多,均可推广
C.甲的平均亩产量较高,且亩产量比较稳定,应推广甲
D.甲、乙的平均亩产量相差不多,但乙的亩产量比较稳定,应推广乙
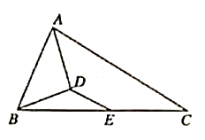
10.如图,△ABC中,AB=6,AC=4,AD是∠BAC的外角平分线,CD⊥AD于D,且点E是BC的中点,则DE为( )
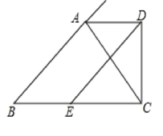
A.8.5 B.8 C.7.5 D.5
二、填空题(本大题共有6小题,每小题3分,共18分)
11.如图,![]() 中,
中,![]() 是
是![]() 的中点,
的中点,![]() 平分
平分![]() ,
,![]() 于点
于点![]() ,若
,若![]() ,
,![]() ,则
,则![]() 的长度为_____.
的长度为_____.
12.菱形ABCD中,对角线AC=8,BD=6,则菱形的边长为_____.
13.我市某一周每天的最低气温统计如下(单位:℃):﹣1,﹣4,6,0,﹣1,1,﹣1,则这组数据的众数为__________.
14.若式子![]() +
+![]() 有意义,则x的取值范围是____.
有意义,则x的取值范围是____.
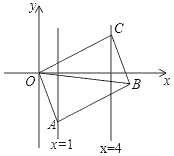
15.如图,已知▱OABC的顶点A、C分别在直线x=1和x=4上,O是坐标原点,则对角线OB长的最小值为__.
16.写出一个经过二、四象限的正比例函数_________________________.
三、解下列各题(本大题共8小题,共72分)
17.(8分)某校为了丰富学生的课外体育活动,购买了排球和跳绳,已知排球的单价是跳绳的单价的3倍,购买跳绳共花费了750元,购买排球共花费900元,购买跳绳的数量比购买排球的数量多30个,求跳绳的单价.
18.(8分)有这样一个问题:探究函数![]()
![]() 的图象与性质,小东根据学习函数的经验,对函数的图象与性质进行了探究,下面是小东的探究过程,请补充完整:
的图象与性质,小东根据学习函数的经验,对函数的图象与性质进行了探究,下面是小东的探究过程,请补充完整:
(1)下表是![]() 与
与![]() 的几组对应值,则
的几组对应值,则![]() .
.
| … |
|
|
|
|
|
|
|
|
| … |
| … |
|
|
|
|
|
|
|
|
| … |
(2)如图,在平面直角坐标系![]() 中,描出了以上表中各对对应值为坐标的点. 根据描出的点,画出该函数的图象;
中,描出了以上表中各对对应值为坐标的点. 根据描出的点,画出该函数的图象;
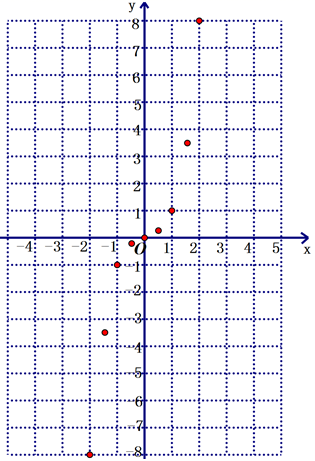
(3)当![]() 时,
时,![]() 随
随![]() 的增大而 ;当
的增大而 ;当![]() 时,
时,![]() 的最小值为 .
的最小值为 .
19.(8分)如图,在正方形![]() 中,点
中,点![]() 、
、![]() 是
是![]() 边上的两点,且
边上的两点,且![]() ,过
,过![]() 作
作![]() 于
于![]() ,分别交
,分别交![]() 、
、![]() 于
于![]() ,
,![]() ,
,![]() 、
、![]() 的延长线相交于
的延长线相交于![]() .
.
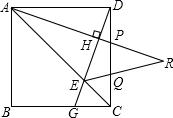
(1)求证:![]() ;
;
(2)判断![]() 的形状,请说明理由.
的形状,请说明理由.
20.(8分)为鼓励学生积极参加体育锻炼,某学校准备购买一批运动鞋供学生借用,现从各年级随机抽取了部分学生所穿运动鞋的号码,绘制了如下的统计图①和图②(不完整).请根据相关信息,解答下列问题:
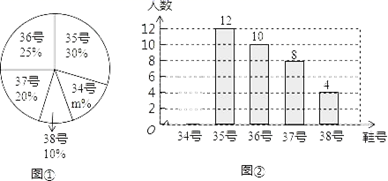
(1)本次接受随机抽样调查的学生人数为 ,图①中m的值为 ;
(2)请补全条形统计图,并求本次调查样本数据的众数和中位数;
(3)根据样本数据,若学校计划购买400双运动鞋,建议购买35号运动鞋多少双?
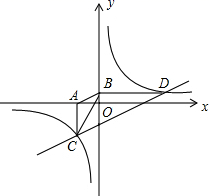
21.(8分)如图,已知双曲线![]() ,经过点D(6,1),点C是双曲线第三象限上的动点,过C作CA⊥x轴,过D作DB⊥y轴,垂足分别为A,B,连接AB,BC.
,经过点D(6,1),点C是双曲线第三象限上的动点,过C作CA⊥x轴,过D作DB⊥y轴,垂足分别为A,B,连接AB,BC.
(1)求k的值;
(2)若△BCD的面积为12,求直线CD的解析式;
(3)判断AB与CD的位置关系,并说明理由.
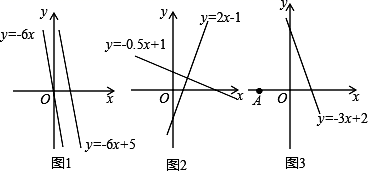
22.(10分)材料一:如图1,由课本91页例2画函数y=﹣6x与y=﹣6x+5可知,直线y=﹣6x+5可以由直线y=﹣6x向上平移5个单位长度得到由此我们得到正确的结论一:在直线L1:y=K1x+b1与直线L2:y=K2x+b2中,如果K1=K2 且b1≠b2 ,那么L1∥L2,反过来,也成立.
材料二:如图2,由课本92页例3画函数y=2x﹣1与y=﹣0.5x+1可知,利用所学知识一定能证出这两条直线是互相垂直的.由此我们得到正确的结论二:在直线L1:y=k1x+b1 与L2:y=k2x+b2 中,如果k1·k2=-1那么L1⊥L2,反过来,也成立
应用举例
已知直线y=﹣![]() x+5与直线y=kx+2互相垂直,则﹣
x+5与直线y=kx+2互相垂直,则﹣![]() k=﹣1.所以k=6
k=﹣1.所以k=6
解决问题
(1)请写出一条直线解析式______,使它与直线y=x﹣3平行.
(2)如图3,点A坐标为(﹣1,0),点P是直线y=﹣3x+2上一动点,当点P运动到何位置时,线段PA的长度最小?并求出此时点P的坐标.
23.(10分)解方程:![]() -
-![]() =1.
=1.
24.(12分)近年来雾霾天气给人们的生活带来很大影响,空气质量问题倍受人们关注,某单位计划在室内安装空气净化装置,需购进A,B两种设备,每台B种设备价格比每台A种设备价格多700元,花3000元购买A种设备和花7200元购买B种设备的数量相同.
(1)求A种、B种设备每台各多少元?
(2)根据单位实际情况,需购进A,B两种设备共20台,总费用不高于17000元,求A种设备至少要购买多少台?
参考答案
一、选择题(每小题3分,共30分)
1、B
2、C
3、D
4、C
5、D
6、A
7、D
8、D
9、D
10、D
二、填空题(本大题共有6小题,每小题3分,共18分)
11、1.
12、5
13、-1
14、2≤x≤3
15、1.
16、y=-2x …(答案不唯一)
三、解下列各题(本大题共8小题,共72分)
17、1元
18、(1)![]() ;(2)详见解析;(3)增大;
;(2)详见解析;(3)增大;![]()
19、(1)见解析;(2)△PQR为等腰三角形,证明过程见解析.
20、 (1) 40,15;(2)见解析;(3)120双
21、(1)k=6;
(2)直线CD的解析式为![]() ;
;
(3)AB∥CD,理由见解析.
22、(1)y=x;(2)当线段PA的长度最小时,点P的坐标为![]() .
.
23、x=–2
24、(1)每台A种设备500元,每台B种设备1元;(2)A种设备至少要购买2台.
2023-2024学年广东省宝塔实验数学九年级第一学期期末质量检测试题含答案: 这是一份2023-2024学年广东省宝塔实验数学九年级第一学期期末质量检测试题含答案,共7页。试卷主要包含了二次函数y=ax2+bx+c,下列事件中,随机事件是,如图,△∽△,若,,,则的长是等内容,欢迎下载使用。
广东省宝塔实验2023-2024学年八上数学期末达标检测试题含答案: 这是一份广东省宝塔实验2023-2024学年八上数学期末达标检测试题含答案,共8页。试卷主要包含了在 ,,,,中,分式的个数是等内容,欢迎下载使用。
2023-2024学年广东省宝塔实验数学八上期末达标测试试题含答案: 这是一份2023-2024学年广东省宝塔实验数学八上期末达标测试试题含答案,共6页。试卷主要包含了下面是一名学生所做的4道练习题等内容,欢迎下载使用。












