


广东省东莞市长安中学2022-2023学年七下数学期末调研试题含答案
展开
这是一份广东省东莞市长安中学2022-2023学年七下数学期末调研试题含答案,共7页。试卷主要包含了当x=1时,下列式子无意义的是,式子,,,,中是分式的有等内容,欢迎下载使用。
广东省东莞市长安中学2022-2023学年七下数学期末调研试题(时间:120分钟 分数:120分) 学校_______ 年级_______ 姓名_______ 注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案标号。回答非选择题时,将答案写在答题卡上,写在本试卷上无效。3.考试结束后,将本试卷和答题卡一并交回。 一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.下列各组图形中不是位似图形的是()A. B.
B.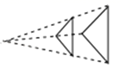 C.
C.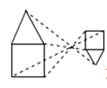 D.
D.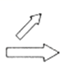 2.菱形OABC在平面直角坐标系中的位置如图所示,若OA = 2,∠AOC = 45°,则B点的坐标是
2.菱形OABC在平面直角坐标系中的位置如图所示,若OA = 2,∠AOC = 45°,则B点的坐标是 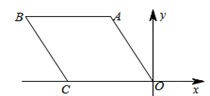 A.(2 +
A.(2 +![]() ,
,![]() ) B.(2﹣
) B.(2﹣![]() ,
,![]() ) C.(﹣2 +
) C.(﹣2 +![]() ,
,![]() ) D.(﹣2﹣
) D.(﹣2﹣![]() ,
,![]() )3.如图所示,在菱形ABCD中,∠A=60°,AB=2,E,F两点分别从A,B两点同时出发,以相同的速度分别向终点B,C移动,连接EF,在移动的过程中,EF的最小值为( )
)3.如图所示,在菱形ABCD中,∠A=60°,AB=2,E,F两点分别从A,B两点同时出发,以相同的速度分别向终点B,C移动,连接EF,在移动的过程中,EF的最小值为( )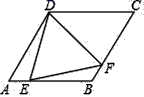 A.1 B.
A.1 B.![]() C.
C.![]() D.
D.![]() 4.如图,菱形ABCD中,E. F分别是AB、AC的中点,若EF=3,则菱形ABCD的周长是( )
4.如图,菱形ABCD中,E. F分别是AB、AC的中点,若EF=3,则菱形ABCD的周长是( )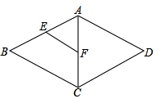 A.12 B.16 C.20 D.245.当x=1时,下列式子无意义的是( )A.
A.12 B.16 C.20 D.245.当x=1时,下列式子无意义的是( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 6.式子
6.式子![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 中是分式的有
中是分式的有![]()
![]() A.1个 B.2个 C.3个 D.4个7.2019年6月7日是端午节,某幼儿园对全体小朋友爱吃哪种粽子做调查,以决定最终买哪种口味的粽子.下面的调查数据最值得关注的是( )A.众数 B.中位数 C.平均数 D.方差8.下列等式从左到右的变形,属于因式分解的是( )A.
A.1个 B.2个 C.3个 D.4个7.2019年6月7日是端午节,某幼儿园对全体小朋友爱吃哪种粽子做调查,以决定最终买哪种口味的粽子.下面的调查数据最值得关注的是( )A.众数 B.中位数 C.平均数 D.方差8.下列等式从左到右的变形,属于因式分解的是( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 9.如图,点P是边长为1的菱形ABCD对角线AC上的一个动点,点M,N分别是AB,BC边上的中点,则MP+PN的最小值是( )
9.如图,点P是边长为1的菱形ABCD对角线AC上的一个动点,点M,N分别是AB,BC边上的中点,则MP+PN的最小值是( )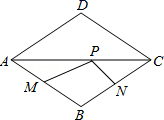 A.
A.![]() B.1 C.
B.1 C.![]() D.210.如图,直线y1=kx+b过点A(0,2),且与直线y2=mx交于点P(1,m),则不等式组
D.210.如图,直线y1=kx+b过点A(0,2),且与直线y2=mx交于点P(1,m),则不等式组![]() 的解集是( )
的解集是( )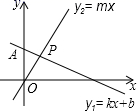 A.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 11.如图,已知菱形ABCD的周长是24米,∠BAC=30°,则对角线BD的长等于()
11.如图,已知菱形ABCD的周长是24米,∠BAC=30°,则对角线BD的长等于()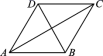 A.6
A.6![]() 米 B.3
米 B.3![]() 米 C.6米 D.3米12.函数y=kx+1与函数y=
米 C.6米 D.3米12.函数y=kx+1与函数y=![]() 在同一坐标系中的大致图象是( )A.
在同一坐标系中的大致图象是( )A.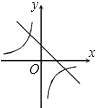 B.
B.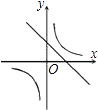 C.
C.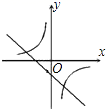 D.
D.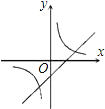 二、填空题(每题4分,满分20分,将答案填在答题纸上)13.如图,它是个数值转换机,若输入的a值为
二、填空题(每题4分,满分20分,将答案填在答题纸上)13.如图,它是个数值转换机,若输入的a值为![]() ,则输出的结果应为____.
,则输出的结果应为____.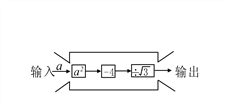 14.如图,直线
14.如图,直线![]() 交
交![]() 轴于点
轴于点![]() ,交
,交![]() 轴于点
轴于点![]() ,
,![]() 是直线
是直线![]() 上的一个动点,过点
上的一个动点,过点![]() 作
作![]() 轴于点
轴于点![]() ,
,![]() 轴于点
轴于点![]() ,
,![]() 的长的最小值为__________.
的长的最小值为__________.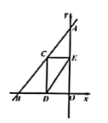 15.如图1,四边形ABCD中,AB∥CD,∠B=90°,AC=AD.动点P从点B出发沿折线B-A-D-C方向以1单位/秒的速度匀速运动,在整个运动过程中,△BCP的面积S与运动时间t(秒)的函数图象如图2所示,写出①AB=__________;②CD=_______________(提示:过A作CD的垂线);③BC=_______________.
15.如图1,四边形ABCD中,AB∥CD,∠B=90°,AC=AD.动点P从点B出发沿折线B-A-D-C方向以1单位/秒的速度匀速运动,在整个运动过程中,△BCP的面积S与运动时间t(秒)的函数图象如图2所示,写出①AB=__________;②CD=_______________(提示:过A作CD的垂线);③BC=_______________.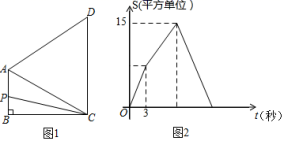 16.如图,在▱ABCD中,若∠A=63°,则∠D=_____.
16.如图,在▱ABCD中,若∠A=63°,则∠D=_____.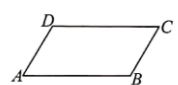 17.不等式组
17.不等式组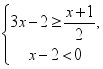 的解集是________;三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)18.(5分)如图,已知AB是⊙O的直径,AC是弦,直线EF经过点C,AD⊥EF于点D,∠DAC=∠BAC.
的解集是________;三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)18.(5分)如图,已知AB是⊙O的直径,AC是弦,直线EF经过点C,AD⊥EF于点D,∠DAC=∠BAC.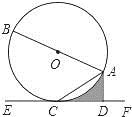 (1)求证:EF是⊙O的切线;(2)若⊙O的半径为2,∠ACD=30°,求图中阴影部分的面积. 19.(5分)如图,等边△ABC的边长是2,D、E分别为AB、AC的中点,过点E作EF∥CD交BC的延长线于点F,连接CD.(1)求证:DE=CF;(2)求EF的长.
(1)求证:EF是⊙O的切线;(2)若⊙O的半径为2,∠ACD=30°,求图中阴影部分的面积. 19.(5分)如图,等边△ABC的边长是2,D、E分别为AB、AC的中点,过点E作EF∥CD交BC的延长线于点F,连接CD.(1)求证:DE=CF;(2)求EF的长.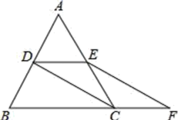 20.(8分)解方程(1)
20.(8分)解方程(1)![]() (2)
(2)![]() (3)
(3)![]() 21.(10分)某研究性学习小组在探究矩形的折纸问题时,将一块直角三角板的直角顶点绕矩形ABCD(AB<BC)的对角线的交点O旋转(①→②→③),图中的M、N分别为直角三角形的直角边与矩形ABCD的边CD、BC的交点.
21.(10分)某研究性学习小组在探究矩形的折纸问题时,将一块直角三角板的直角顶点绕矩形ABCD(AB<BC)的对角线的交点O旋转(①→②→③),图中的M、N分别为直角三角形的直角边与矩形ABCD的边CD、BC的交点.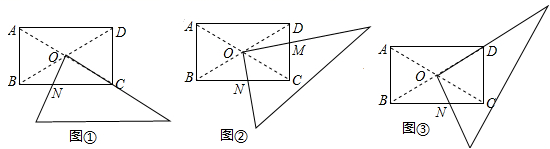 (1)该学习小组成员意外的发现图①中(三角板一边与CC重合),BN、CN、CD这三条线段之间存在一定的数量关系:CN2=BN2+CD2,请你对这名成员在图①中发现的结论说明理由;(2)在图③中(三角板一直角边与OD重合),试探究图③中BN、CN、CD这三条线段之间的数量关系,直接写出你的结论.(3)试探究图②中BN、CN、CM、DM这四条线段之间的数量关系,写出你的结论,并说明理由. 22.(10分)某校八年级数学实践能力考试选择项目中,选择数据收集项目和数据分析项目的学生比较多。为了解学生数据收集和数据分析的水平情况,进行了抽样调查,过程如下,请补充完整.收集数据:从选择数据收集和数据分析的学生中各随机抽取16人,进行了体育测试,测试成绩(十分制)如下:数据收集109.59.510899.5971045.5107.99.510数据分析9.598.58.5109.510869.5109.598.59.56整理,描述数据:按如下分数段整理,描述这两组样本数据:
(1)该学习小组成员意外的发现图①中(三角板一边与CC重合),BN、CN、CD这三条线段之间存在一定的数量关系:CN2=BN2+CD2,请你对这名成员在图①中发现的结论说明理由;(2)在图③中(三角板一直角边与OD重合),试探究图③中BN、CN、CD这三条线段之间的数量关系,直接写出你的结论.(3)试探究图②中BN、CN、CM、DM这四条线段之间的数量关系,写出你的结论,并说明理由. 22.(10分)某校八年级数学实践能力考试选择项目中,选择数据收集项目和数据分析项目的学生比较多。为了解学生数据收集和数据分析的水平情况,进行了抽样调查,过程如下,请补充完整.收集数据:从选择数据收集和数据分析的学生中各随机抽取16人,进行了体育测试,测试成绩(十分制)如下:数据收集109.59.510899.5971045.5107.99.510数据分析9.598.58.5109.510869.5109.598.59.56整理,描述数据:按如下分数段整理,描述这两组样本数据: ![]()
![]()
![]()
![]() 10数据收集11365数据分析 (说明:成绩8.5分及以上为优秀,6分及以上为合格,6分以下为不合格.)分析数据:两组样本数据的平均数,中位数,众数如下表所示:项目平均数中位数众数数据收集8.759.510数据分析8.819.259.5得出结论:(1)如果全校有480人选择数据收集项目,达到优秀的人数约为________人;(2)初二年级的井航和凯舟看到上面数据后,井航说:数据分析项目整体水平较高.凯舟说:数据收集项目整体水平较高.你同意________的看法,理由为_______________________.(至少从两个不同的角度说明推断的合理性) 23.(12分)如图1,已知四边形ABCD是正方形,对角线AC、BD相交于点E,以点E为顶点作正方形EFGH.(1)如图1,点A、D分别在EH和EF上,连接BH、AF,BH和AF有何数量关系,并说明理由;(2)将正方形EFGH绕点E顺时针方向旋转,如图2,判断BH和AF的数量关系,并说明理由.
10数据收集11365数据分析 (说明:成绩8.5分及以上为优秀,6分及以上为合格,6分以下为不合格.)分析数据:两组样本数据的平均数,中位数,众数如下表所示:项目平均数中位数众数数据收集8.759.510数据分析8.819.259.5得出结论:(1)如果全校有480人选择数据收集项目,达到优秀的人数约为________人;(2)初二年级的井航和凯舟看到上面数据后,井航说:数据分析项目整体水平较高.凯舟说:数据收集项目整体水平较高.你同意________的看法,理由为_______________________.(至少从两个不同的角度说明推断的合理性) 23.(12分)如图1,已知四边形ABCD是正方形,对角线AC、BD相交于点E,以点E为顶点作正方形EFGH.(1)如图1,点A、D分别在EH和EF上,连接BH、AF,BH和AF有何数量关系,并说明理由;(2)将正方形EFGH绕点E顺时针方向旋转,如图2,判断BH和AF的数量关系,并说明理由.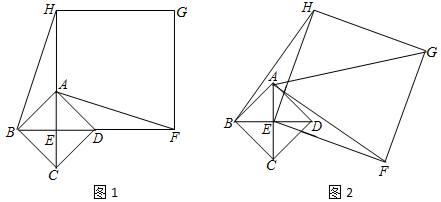 参考答案 一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.1、D2、D3、D4、D5、C6、B7、A8、C9、B10、A11、C12、A 二、填空题(每题4分,满分20分,将答案填在答题纸上)13、-
参考答案 一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.1、D2、D3、D4、D5、C6、B7、A8、C9、B10、A11、C12、A 二、填空题(每题4分,满分20分,将答案填在答题纸上)13、-![]() 14、4.315、1 6 2 16、117°17、1≤x<2 三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)18、(1)见解析;(2)
14、4.315、1 6 2 16、117°17、1≤x<2 三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)18、(1)见解析;(2)![]() 19、 (1)见解析;(2)
19、 (1)见解析;(2)![]() .20、(1)
.20、(1)![]() (2)
(2)![]() (3)
(3)![]() 21、 (1)见解析;(1)BN1=NC1+CD1;(3)CM1+CN1=DM1+BN1,理由见解析.22、(1)1;(2)凯舟,数据收集项目的中位数较大,众数也较大,因此数据收集项目的整体水平较高.23、(1)BH=AF,见解析;(2)BH=AF,见解析.
21、 (1)见解析;(1)BN1=NC1+CD1;(3)CM1+CN1=DM1+BN1,理由见解析.22、(1)1;(2)凯舟,数据收集项目的中位数较大,众数也较大,因此数据收集项目的整体水平较高.23、(1)BH=AF,见解析;(2)BH=AF,见解析.
相关试卷
这是一份2023-2024学年广东省东莞市长安中学数学九年级第一学期期末调研试题含答案,共8页。试卷主要包含了下列图形中是中心对称图形的有个,已知点A等内容,欢迎下载使用。
这是一份广东省东莞市长安实验中学2023-2024学年数学九上期末检测试题含答案,共8页。试卷主要包含了二次函数y=3等内容,欢迎下载使用。
这是一份广东省东莞市长安中学2023-2024学年数学八上期末考试模拟试题含答案,共8页。试卷主要包含了在平面直角坐标系中,点P,如图,图形中x的值为等内容,欢迎下载使用。









