


广东省佛山市高明区2022-2023学年七年级数学第二学期期末达标检测试题含答案
展开
这是一份广东省佛山市高明区2022-2023学年七年级数学第二学期期末达标检测试题含答案,共7页。试卷主要包含了化简的结果是,已知,,则的结果为,使式子有意义的条件是等内容,欢迎下载使用。
广东省佛山市高明区2022-2023学年七年级数学第二学期期末达标检测试题(时间:120分钟 分数:120分) 学校_______ 年级_______ 姓名_______ 请考生注意:1.请用2B铅笔将选择题答案涂填在答题纸相应位置上,请用0.5毫米及以上黑色字迹的钢笔或签字笔将主观题的答案写在答题纸相应的答题区内。写在试题卷、草稿纸上均无效。2.答题前,认真阅读答题纸上的《注意事项》,按规定答题。 一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.如图,将△ABC绕点B逆时针旋转α,得到△EBD,若点A恰好在ED的延长线上,则∠CAD的度数为( )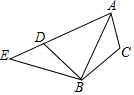 A.90°﹣α B.α C.180°﹣α D.2α2.顺次连接一个四边形的各边中点,得到了一个矩形,则下列四边形中满足条件的是( )①平行四边形;②菱形;③矩形;④对角线互相垂直的四边形.A.①③ B.②③ C.③④ D.②④3.化简
A.90°﹣α B.α C.180°﹣α D.2α2.顺次连接一个四边形的各边中点,得到了一个矩形,则下列四边形中满足条件的是( )①平行四边形;②菱形;③矩形;④对角线互相垂直的四边形.A.①③ B.②③ C.③④ D.②④3.化简![]() 的结果是( )A.2 B.
的结果是( )A.2 B.![]() C.4 D.164.已知
C.4 D.164.已知![]() ,
,![]() ,则
,则![]() 的结果为( )A.
的结果为( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 5.为了调查某种小麦的长势,从中抽取了10株麦苗,测得苗高(单位:
5.为了调查某种小麦的长势,从中抽取了10株麦苗,测得苗高(单位:![]() )为16,9,14,11,12,10,16,8,17,19,则这组数据的中位数和众数分别是( )A.11,11 B.12,11 C.13,11 D.13,166.使式子
)为16,9,14,11,12,10,16,8,17,19,则这组数据的中位数和众数分别是( )A.11,11 B.12,11 C.13,11 D.13,166.使式子![]() 有意义的条件是( )A.x≥4 B.x=4 C.x≤4 D.x≠47.如图,点
有意义的条件是( )A.x≥4 B.x=4 C.x≤4 D.x≠47.如图,点![]() ,
,![]() ,
,![]() ,
,![]() 在一次函数
在一次函数![]() 的图象上,它们的横坐标分别是-1,0,3,7,分别过这些点作
的图象上,它们的横坐标分别是-1,0,3,7,分别过这些点作![]() 轴、
轴、![]() 轴的垂线,得到三个矩形,那么这三个矩形的周长和为( )
轴的垂线,得到三个矩形,那么这三个矩形的周长和为( )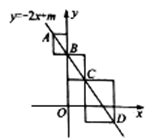 A.
A.![]() B.52 C.48 D.
B.52 C.48 D.![]() 8.如果把分式
8.如果把分式![]() 中x、y的值都扩大为原来的2倍,则分式的值( )A.扩大为原来的4 倍 B.扩大为原来的2倍C.不变 D.缩小为原来的
中x、y的值都扩大为原来的2倍,则分式的值( )A.扩大为原来的4 倍 B.扩大为原来的2倍C.不变 D.缩小为原来的![]() 9.用配方法解一元二次方程
9.用配方法解一元二次方程![]() ,下列配方正确的是( )A.
,下列配方正确的是( )A.![]() B.
B.![]() C.
C.![]() D.
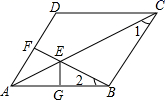
D.![]() 10.如图,F是菱形ABCD的边AD的中点,AC与BF相交于E,
10.如图,F是菱形ABCD的边AD的中点,AC与BF相交于E,![]() 于G,已知
于G,已知![]() ,则下列结论:
,则下列结论:![]() ;
;![]() ;
;![]() :
:![]() 其中正确的结论是
其中正确的结论是![]()
![]()
 A.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 11.如图,任意转动正六边形转盘一次,当转盘停止转动时,指针指向大于3的数的概率是( )
11.如图,任意转动正六边形转盘一次,当转盘停止转动时,指针指向大于3的数的概率是( )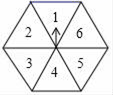 A.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 12.计算
12.计算![]() ÷
÷![]() 的结果是( )A.
的结果是( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 二、填空题(每题4分,满分20分,将答案填在答题纸上)13.在菱形
二、填空题(每题4分,满分20分,将答案填在答题纸上)13.在菱形![]() 中,
中,![]() ,
,![]() 为
为![]() 中点,
中点,![]() 为对角线
为对角线![]() 上一动点,连结
上一动点,连结![]() 和
和![]() ,则
,则![]() 的值最小为_______.14.一个矩形在直角坐标平面上的三个顶点的坐标分别是(﹣2,﹣1)、(3,﹣1)、(﹣2,3),那么第四个顶点的坐标是_____.15.若直线y=kx+b与直线y=2x平行,且与y轴相交于点(0,–3),则直线的函数表达式是__________.16.如图,在平面直角坐标系xOy中,A是双曲线
的值最小为_______.14.一个矩形在直角坐标平面上的三个顶点的坐标分别是(﹣2,﹣1)、(3,﹣1)、(﹣2,3),那么第四个顶点的坐标是_____.15.若直线y=kx+b与直线y=2x平行,且与y轴相交于点(0,–3),则直线的函数表达式是__________.16.如图,在平面直角坐标系xOy中,A是双曲线![]() 在第一象限的分支上的一个动点,连接AO并延长与这个双曲线的另一分支交于点B,以AB为底边作等腰直角三角形ABC,使得点C位于第四象限。(1)点C与原点O的最短距离是________;(2)没点C的坐标为(
在第一象限的分支上的一个动点,连接AO并延长与这个双曲线的另一分支交于点B,以AB为底边作等腰直角三角形ABC,使得点C位于第四象限。(1)点C与原点O的最短距离是________;(2)没点C的坐标为(![]() ,点A在运动的过程中,y随x的变化而变化,y关于x的函数关系式为________。
,点A在运动的过程中,y随x的变化而变化,y关于x的函数关系式为________。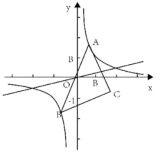 17.如图,在平面直角坐标系中,点A1,A2,A3…和B1,B2,B3,…分别在直线y=
17.如图,在平面直角坐标系中,点A1,A2,A3…和B1,B2,B3,…分别在直线y=![]() x+b和x轴上.△OA1B1,△B1A2B2,△B2A3B3,…都是等腰直角三角形如果点A1(1,1),那么点A2019的纵坐标是_____.
x+b和x轴上.△OA1B1,△B1A2B2,△B2A3B3,…都是等腰直角三角形如果点A1(1,1),那么点A2019的纵坐标是_____.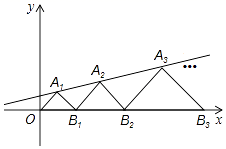 三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)18.(5分)如图,等边△ABC的边长是2,D、E分别为AB、AC的中点,延长BC至点F,使CF=
三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)18.(5分)如图,等边△ABC的边长是2,D、E分别为AB、AC的中点,延长BC至点F,使CF=![]() BC,连结CD和EF.(1)求证:四边形CDEF是平行四边形;(2)求四边形BDEF的周长.
BC,连结CD和EF.(1)求证:四边形CDEF是平行四边形;(2)求四边形BDEF的周长.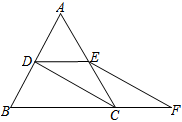 19.(5分)已知:点O到△ABC的两边AB,AC所在直线的距离相等,且OB=OC.(1)如图1,若点O在边BC上,OE⊥AB,OF⊥AC,垂足分别为E,F.求证:AB=AC;
19.(5分)已知:点O到△ABC的两边AB,AC所在直线的距离相等,且OB=OC.(1)如图1,若点O在边BC上,OE⊥AB,OF⊥AC,垂足分别为E,F.求证:AB=AC;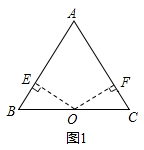 (2)如图,若点O在△ABC的内部,求证:AB=AC;
(2)如图,若点O在△ABC的内部,求证:AB=AC;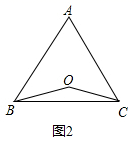 (3)若点O在△ABC的外部,AB=AC成立吗?请画出图表示. 20.(8分)如图1,点A(a,b)在平面直角坐标系xOy中,点A到坐标轴的垂线段AB,AC与坐标轴围成矩形OBAC,当这个矩形的一组邻边长的和与积相等时,点A称作“垂点”,矩形称作“垂点矩形”.(1)在点P(1,2),Q(2,-2),N(
(3)若点O在△ABC的外部,AB=AC成立吗?请画出图表示. 20.(8分)如图1,点A(a,b)在平面直角坐标系xOy中,点A到坐标轴的垂线段AB,AC与坐标轴围成矩形OBAC,当这个矩形的一组邻边长的和与积相等时,点A称作“垂点”,矩形称作“垂点矩形”.(1)在点P(1,2),Q(2,-2),N(![]() ,-1)中,是“垂点”的点为 ;(2)点M(-4,m)是第三象限的“垂点”,直接写出m的值 ;(3)如果“垂点矩形”的面积是
,-1)中,是“垂点”的点为 ;(2)点M(-4,m)是第三象限的“垂点”,直接写出m的值 ;(3)如果“垂点矩形”的面积是![]() ,且“垂点”位于第二象限,写出满足条件的“垂点”的坐标 ;(4)如图2,平面直角坐标系的原点O是正方形DEFG的对角线的交点,当正方形DEFG的边上存在“垂点”时,GE的最小值为 .
,且“垂点”位于第二象限,写出满足条件的“垂点”的坐标 ;(4)如图2,平面直角坐标系的原点O是正方形DEFG的对角线的交点,当正方形DEFG的边上存在“垂点”时,GE的最小值为 .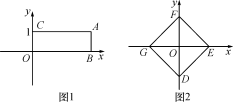 21.(10分)如图,在平面直角坐标系中,正方形ABCD的顶点A在y轴正半轴上,顶点B在x轴正半轴上,OA、OB的长分别是一元二次方程x2﹣7x+12=0的两个根(OA>OB).(1)求点D的坐标.(2)求直线BC的解析式.(3)在直线BC上是否存在点P,使△PCD为等腰三角形?若存在,请直接写出点P的坐标;若不存在,说明理由.
21.(10分)如图,在平面直角坐标系中,正方形ABCD的顶点A在y轴正半轴上,顶点B在x轴正半轴上,OA、OB的长分别是一元二次方程x2﹣7x+12=0的两个根(OA>OB).(1)求点D的坐标.(2)求直线BC的解析式.(3)在直线BC上是否存在点P,使△PCD为等腰三角形?若存在,请直接写出点P的坐标;若不存在,说明理由.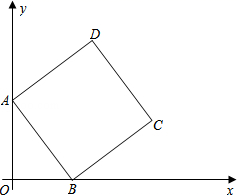 22.(10分)如图,矩形
22.(10分)如图,矩形![]() 中,点
中,点![]() 是线段
是线段![]() 上一动点,
上一动点, ![]() 为
为![]() 的中点,
的中点, ![]() 的延长线交BC于
的延长线交BC于![]() .
.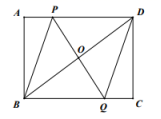 (1)求证:
(1)求证: ![]() ;(2)若
;(2)若![]() ,
,![]() ,
,![]() 从点
从点![]() 出发,以l
出发,以l![]() 的速度向
的速度向![]() 运动(不与
运动(不与![]() 重合).设点
重合).设点![]() 运动时间为
运动时间为![]() ,请用
,请用![]() 表示
表示![]() 的长;并求
的长;并求![]() 为何值时,四边形
为何值时,四边形![]() 是菱形. 23.(12分)如图,△ABC与△AFD为等腰直角三角形,∠FAD=∠BAC=90°,点D在BC上,则:(1)求证:BF=DC.(2)若BD=AC,则求∠BFD的度数.
是菱形. 23.(12分)如图,△ABC与△AFD为等腰直角三角形,∠FAD=∠BAC=90°,点D在BC上,则:(1)求证:BF=DC.(2)若BD=AC,则求∠BFD的度数.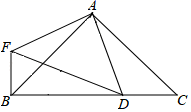 参考答案 一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.1、C2、D3、A4、B5、D6、A7、C8、B9、A10、A11、D12、C 二、填空题(每题4分,满分20分,将答案填在答题纸上)13、2
参考答案 一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.1、C2、D3、A4、B5、D6、A7、C8、B9、A10、A11、D12、C 二、填空题(每题4分,满分20分,将答案填在答题纸上)13、2![]() 14、(3,3)15、y=2x–116、
14、(3,3)15、y=2x–116、![]()
![]() 17、
17、![]() 三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)18、(1)证明见解析;(2)5+
三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)18、(1)证明见解析;(2)5+![]() .19、(1)见解析;(2)见解析;(3)不一定成立,见解析.20、(1)Q;(2)-
.19、(1)见解析;(2)见解析;(3)不一定成立,见解析.20、(1)Q;(2)-![]() ;(3)(-4,
;(3)(-4,![]() ),(-
),(-![]() ,4);(4)121、(1)D(4,7)(2)y=
,4);(4)121、(1)D(4,7)(2)y=![]() (3)详见解析22、 (1)证明见解析;(2) PD=8-t,运动时间为
(3)详见解析22、 (1)证明见解析;(2) PD=8-t,运动时间为![]() 秒时,四边形PBQD是菱形.23、(1)见解析;(2)67.5°.
秒时,四边形PBQD是菱形.23、(1)见解析;(2)67.5°.
相关试卷
这是一份2023-2024学年广东省佛山市高明区九上数学期末学业质量监测试题含答案,共8页。试卷主要包含了考生必须保证答题卡的整洁,若分式的值为,则的值为,二次函数y=x2+等内容,欢迎下载使用。
这是一份2023-2024学年广东省佛山市高明区九上数学期末考试模拟试题含答案,共7页。试卷主要包含了方程x2﹣9=0的解是,下列方程中,是一元二次方程的是,下列图形中是中心对称图形的有个等内容,欢迎下载使用。
这是一份广东省佛山市高明区2023-2024学年八上数学期末质量检测模拟试题含答案,共8页。试卷主要包含了答题时请按要求用笔,如图所示,在中,,则为,如图,已知,下列结论等内容,欢迎下载使用。








