广东省佛山市顺德区容桂中学2022-2023学年数学七年级第二学期期末统考试题含答案

这是一份广东省佛山市顺德区容桂中学2022-2023学年数学七年级第二学期期末统考试题含答案，共7页。试卷主要包含了下列调查方式中适合的是，下列事件等内容，欢迎下载使用。
广东省佛山市顺德区容桂中学2022-2023学年数学七年级第二学期期末统考试题（时间：120分钟             分数：120分） 学校_______            年级_______        姓名_______ 请考生注意：1．请用2B铅笔将选择题答案涂填在答题纸相应位置上，请用0．5毫米及以上黑色字迹的钢笔或签字笔将主观题的答案写在答题纸相应的答题区内。写在试题卷、草稿纸上均无效。2．答题前，认真阅读答题纸上的《注意事项》，按规定答题。 一、选择题(每小题3分,共30分)1．如图，已知正方形ABCD的边长为5，E为BC边上的一点，∠EBC=30°，则BE的长为 ( 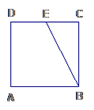  )A．cm B．2cm  C．5 cm D．10 cm2．如图，在中，分别以点为圆心，大于长为半径作弧，两弧交于点，作直线分别交，于点，连接，下列结论错误的是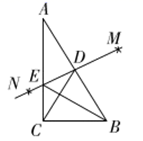（  ）A． B． C． D．平分3．下列调查方式中适合的是（    ）A．要了解一批节能灯的使用寿命，采用普查方式B．调查你所在班级同学的身高，采用抽样调查方式C．环保部门调查长江某段水域的水质情况，采用抽样调查方式D．调查全市中学生每天的就寝时间，采用普查方式4．为了解某种电动汽车一次充电后行驶的里程数，抽检了10辆车，统计结果如图所示，则在一次充电后行驶的里程数这组数据中，众数和中位数分别是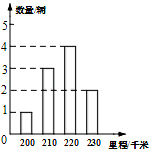（　　）A．220，220 B．220，210 C．200，220 D．230，2105．下列各点中，不在反比例函数图象上的点是（    ）A． B． C． D．6．将0.000008这个数用科学记数法表示为（   ）A．8×10-6 B．8×10-5 C．0.8×10-5 D．8×10-77．已知关于x的方程的解是正数，那么m的取值范围为（　　）A．m＞－6且m≠2 B．m＜6 C．m＞－6且m≠－4 D．m＜6且m≠－28．已知一个多边形的内角和是它的外角和的两倍，那么它的边数为（    ）A．8 B．6 C．5 D．49．等边三角形的边长为2，则该三角形的面积为（   ）A． B．2 C．3 D．410．下列事件：①上海明天是晴天，②铅球浮在水面上，③平面中，多边形的外角和都等于360度，属于确定事件的个数有（　　）A．0个 B．1个 C．2个 D．3个二、填空题(本大题共有6小题，每小题3分，共18分)11．若二次函数y=ax2+bx的图象开口向下，则a可以为_________（写出一个即可）．12．一次函数y=-x-1的图象不经过第_____象限．13．有10个数据的平均数为12，另有20个数据的平均数为15，那么所有这30个数据的平均数是________．14．一直角三角形的两条直角边分别是4cm和3cm，则其斜边上中线的长度为 ___________.15．一天，小明放学骑车从学校出发路过新华书店买了一本课外书再骑车回家，他所行驶的路程s与时间t的关系如图，则经18分钟后，小明离家还有____千米.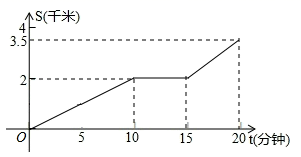16．一组数据按从小到大顺序排列为：3，5，7，8，8，则这组数据的中位数是     ，众数是     .三、解下列各题(本大题共8小题，共72分)17．（8分）利用对称性可设计出美丽的图案．在边长为1的方格纸中,有如图所示的四边形(顶点都在格点上)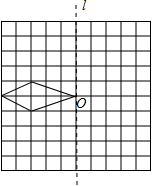．   (1)先作出该四边形关于直线成轴对称的图形，再作出你所作的图形连同原四边形绕0点按顺时针方向旋转90o后的图形；(2)完成上述设计后，整个图案的面积等于_________．   18．（8分）以四边形ABCD的边AB，AD为边分别向外侧作等边三角形ABF和等边三角形ADE，连接EB，FD，交点为G．（1）当四边形ABCD为正方形时，如图①，EB和FD的数量关系是　   　；（2）当四边形ABCD为矩形时，如图②，EB和FD具有怎样的数量关系？请加以证明；（3）如图③，四边形ABCD由正方形到矩形再到一般平行四边形的变化过程中，EB和FD具有怎样的数量关系？请直接写出结论，无需证明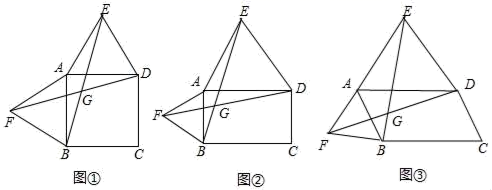．   19．（8分）先化简，再求值：（+）÷，其中x=﹣1．   20．（8分）如图，在□ABCD中，E、F分别是AB、CD的中点．（1）求证：四边形EBFD为平行四边形；（2）对角线AC分别与DE、BF交于点M、N.求证：△ABN≌△CDM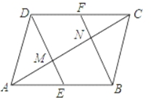．   21．（8分）如图，直线y＝﹣x+3与x轴相交于点B，与y轴相交于点A，点E为线段AB中点，∠ABO的平分线BD与y轴相较于点D，点A、C关于点O对称．（1）求线段DE的长；（2）一个动点P从点D出发，沿适当的路径运动到直线BC上的点F，再沿射线CB方向移动2个单位到点G，最后从点G沿适当的路径运动到点E处，当P的运动路径最短时，求此时点G的坐标；（3）将△ADE绕点A顺时针方向旋转，旋转角度α（0＜α≤180°），在旋转过程中DE所在的直线分别与直线BC、直线AC相交于点M、点N，是否存在某一时刻使△CMN为等腰三角形，若存在，请求出CM的长，若不存在，请说明理由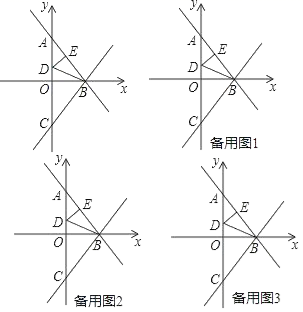．   22．（10分）如图，在平面直角坐标系内，小正方形网格的边长为1个单位长度，的三个顶点的坐标分别为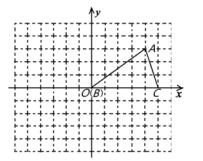，，．（1）画出将向上平移2个单位长度，再向左平移5个单位长度后得到的；（2）画出将绕点按顺时针方向旋转90°得到的；（3）在轴上存在一点，满足点到点与点的距离之和最小，请直接写出点的坐标．   23．（10分）某单位招聘员工，采取笔试与面试相结合的方式进行，两项成绩的原始分均为100分．前6名选手的得分如下：　　　　序号项目123456笔试成绩/分859284908480面试成绩/分908886908085根据规定，笔试成绩和面试成绩分别按一定的百分比折合成综合成绩(综合成绩的满分仍为100分)．（1）这6名选手笔试成绩的中位数是________分，众数是________分；（2）现得知1号选手的综合成绩为88分，求笔试成绩和面试成绩各占的百分比；（3）求出其余五名选手的综合成绩，并以综合成绩排序确定前两名人选．   24．（12分）两个含有二次根式的代数式相乘，积不含有二次根式，称这两个代数式互为有理化因式，例如: 与、与等都是互为有理化因式，在进行二次根式计算时，利用有理化因式，可以化去分母中的根号.例如: ；；…….请仿照上述过程，化去下列各式分母中的根号. (1) (2) (n为正整数).   参考答案 一、选择题(每小题3分,共30分)1、D2、D3、C4、A5、A6、A7、C8、B9、A10、C 二、填空题(本大题共有6小题，每小题3分，共18分)11、a＝−2（答案不唯一）12、一．13、14.14、cm15、0.116、7    1 三、解下列各题(本大题共8小题，共72分)17、（1）图见解析； （2）118、（1）DF＝BE；（2）EB＝FD，证明见解析；（3）DF＝BE19、-5.20、（1）证明见解析；（2）证明见解析.21、（1）1；（2）（，）；（3）6+﹣3或6++3或2﹣2或8.22、（1）答案见解析；（2）答案见解析；（3）．23、（1）84.5，84；（2）笔试成绩和面试成绩所占的百分比分别是40%，60%；（3）综合成绩排序前两名的人选是4号和2号选手．24、（1）；（2）.