


广东省广州大附中2022-2023学年七年级数学第二学期期末学业质量监测模拟试题含答案
展开这是一份广东省广州大附中2022-2023学年七年级数学第二学期期末学业质量监测模拟试题含答案,共7页。试卷主要包含了已知点是平行四边形内一点,设等内容,欢迎下载使用。
广东省广州大附中2022-2023学年七年级数学第二学期期末学业质量监测模拟试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
考生须知:
1.全卷分选择题和非选择题两部分,全部在答题纸上作答。选择题必须用2B铅笔填涂;非选择题的答案必须用黑色字迹的钢笔或答字笔写在“答题纸”相应位置上。
2.请用黑色字迹的钢笔或答字笔在“答题纸”上先填写姓名和准考证号。
3.保持卡面清洁,不要折叠,不要弄破、弄皱,在草稿纸、试题卷上答题无效。
一、选择题(每小题3分,共30分)
1.如图,菱形![]() 的对角线
的对角线![]() 、
、![]() 相交于点
相交于点![]() ,
,![]() ,
,![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,连接
,连接![]() ,则
,则![]() 的长为( )
的长为( )
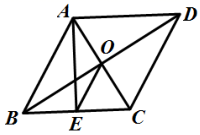
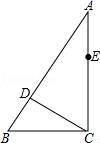
A.![]() B.2 C.3 D.6
B.2 C.3 D.6
2.以下列各组数据中的三个数作为三角形的边长,其中能构成直角三角形的是![]()
![]()
A.2,3,4 B.![]() ,
,![]() ,
,![]() C.
C.![]() ,
,![]() ,1 D.6,9,13
,1 D.6,9,13
3.如图是某公司今年1~5月份的收入统计表(有污染,若2月份,3月份的增长率相同,设它们的增长率为x,根据表中信息,可列方程为( )
月份 | 1 | 2 | 3 | 4 | 5 |
收入/万元 | 1 | ▄ | 4 | 5 | ▄ |
A.(1+x)2=4﹣1 B.(1+x)2=4
C.(1+2x)2=7 D.(1+x)(1+2x)=4
4.下列各点中,在正比例函数![]() 的图象上的点是( )
的图象上的点是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.已知点![]() 是平行四边形
是平行四边形![]() 内一点(不含边界),设
内一点(不含边界),设![]()
![]()
![]() .若
.若![]()
![]()
![]() ,则( )
,则( )
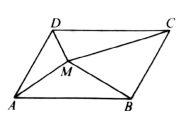
A.![]() B.
B.![]()
C.![]() D.
D.![]()
6.菱形的两条对角线长分别是6cm和8cm,则它的面积是( )
A.6cm2 B.12cm2 C.24cm2 D.48cm2
7.如图,已知Rt△ABC中,∠ACB=90°,AC=6,BC=4,将△ABC绕直角顶点C顺时针旋转90°得到△DEC.若点F是DE的中点,连接AF,则AF=( )
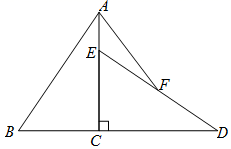
A.4 B.5 C.![]() D.6
D.6
8.下列各组数中,以它们为边长的线段不能构成直角三角形的是( )
A.1,![]() ,
,![]() B.3,4,5 C.5,12,13 D.2,2,3
B.3,4,5 C.5,12,13 D.2,2,3
9.如图1,在矩形ABCD中,动点P从点B出发,沿BC、CD、DA运动至点A停止,设点P运动的路程为x,△ABP的面积为y,如果y关于x的函数图象如图2所示,则△ABC的面积是( )
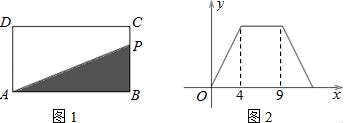
A.10 B.16 C.18 D.20
10.下列各组数中能作为直角三角形的三边长的是( )
A.1,2,3 B.3,4,5 C.4,5,6 D.7,8,9
二、填空题(本大题共有6小题,每小题3分,共18分)
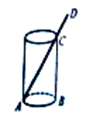
11.一种圆柱形口杯(厚度忽略不计),测得内部底面半径为![]() ,高为
,高为![]() .吸管如图放进杯里,杯口外面露出部分长为
.吸管如图放进杯里,杯口外面露出部分长为![]() ,则吸管
,则吸管![]() 的长度为_____
的长度为_____![]() .
.
12.利用因式分解计算:2012-1992=_________;
13.古语说:“春眠不觉晓”,每到初春时分,想必有不少人变得嗜睡,而且睡醒后精神不佳.我们可以在饮食方面进行防治,比如以下食物可防治春困:香椿、大蒜、韭菜、山药、麦片.春天即将来临时,某商人抓住商机,购进甲、乙、丙三种麦片,已知销售每袋甲种麦片的利润率为10%,每袋乙种麦片的利润率为20%,每袋丙种麦片的利润率为30%,当售出的甲、乙、丙三种麦片的袋数之比为1:3:1时,商人得到的总利润率为22%;当售出的甲、乙、丙三种变片的袋数之比为3:2:1时,商人得到的总利润率为20%:那么当售出的甲、乙、丙三种麦片的袋数之比为2:3;4时,这个商人得到的总利润率为_____(用百分号表最终结果).
14.一组数据3,4,6,8,x的中位数是x,且x是满足不等式组![]() 的整数,则这组数据的平均数是 .
的整数,则这组数据的平均数是 .
15.如图所示,△ABC为等边三角形,D为AB的中点,高AH=10 cm,P为AH上一动点,则PD+PB的最小值为_______cm.
16.为方便市民出行,2019年北京地铁推出了电子定期票,电子定期票在使用有效期限内,支持单人不限次数乘坐北京轨道交通全路网(不含机场线)所有线路,电子定期票包括一日票、二日票、三日票、五日票及七日票共五个种类,价格如下表:
种类 | 一日票 | 二日票 | 三日票 | 五日票 | 七日票 |
单价(元/张) | 20 | 30 | 40 | 70 | 90 |
某人需要连续6天不限次数乘坐地铁,若决定购买电子定期票,则总费用最低为____元.
三、解下列各题(本大题共8小题,共72分)
17.(8分)已知一次函数y=kx+b的图象经过点(3,-3),且与直线y=4x-3的交点在x轴上.
(1)求这个一次函数的解析式.
(2)此函数的图象经过哪几个象限?
(3)求此函数的图象与坐标轴围成的三角形的面积.
18.(8分)已知y+2与3x成正比例,当x=1时,y的值为4.
(1)求y与x之间的函数表达式;
(2)若点(-1,a),(2,b)是该函数图象上的两点,请利用一次函数的性质比较a,b的大小.
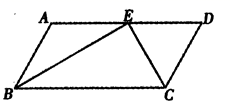
19.(8分)如图,在Rt△ABC中,∠ACB=90°,点D,E分别在AB,AC上,CE=BC,连接CD,将线段CD绕点C按顺时针方向旋转90°后得CF,连接EF
(1)补充完成图形;
(2)若EF∥CD,求证:∠BDC=90°.
20.(8分)运动服装店销售某品牌S号,M号,L号,XL号,XXL号五种不同型号服装,随机统计该品牌运动服装一周的销售情况并绘制如图所示不完整统计图.
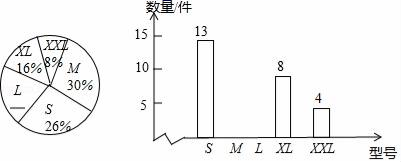
(1)L号运动服一周的销售所占百分比为 .
(2)请补全条形统计图;
(3)服装店老板打算再次购进该品牌服饰共600件,根据各种型号的销售情况,你认为购进XL号约多少件比较合适,请计算说明.
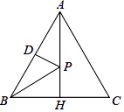
21.(8分)在△ABC中,AH⊥BC于H,D、E、F分别是BC、CA、AB的中点.求证:DE=HF.
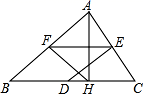
22.(10分)如图所示,平行四边形![]() 中,
中,![]() 和
和![]() 的平分线交于
的平分线交于![]() 边上一点
边上一点![]() ,
,
(1)求![]() 的度数.
的度数.
(2)若![]() ,则平行四边形
,则平行四边形![]() 的周长是多少?
的周长是多少?
23.(10分)如图,在平面直角坐标系![]() 中,矩形
中,矩形![]() 的顶点
的顶点![]() 坐标为
坐标为![]() ,点
,点![]() 在
在![]() 边上从点
边上从点![]() 运动到点
运动到点![]() ,以
,以![]() 为边作正方形
为边作正方形![]() ,连
,连![]() ,在点
,在点![]() 运动过程中,请探究以下问题:
运动过程中,请探究以下问题:
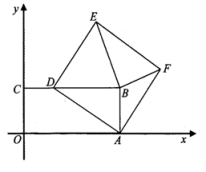
(1)![]() 的面积是否改变,如果不变,求出该定值;如果改变,请说明理由;
的面积是否改变,如果不变,求出该定值;如果改变,请说明理由;
(2)若![]() 为等腰三角形,求此时正方形
为等腰三角形,求此时正方形![]() 的边长.
的边长.
24.(12分)分解因式:
(1)![]() ; (2)
; (2)![]() .
.
参考答案
一、选择题(每小题3分,共30分)
1、C
2、C
3、B
4、C
5、D
6、C
7、B
8、D
9、A
10、B
二、填空题(本大题共有6小题,每小题3分,共18分)
11、17
12、800
13、25%.
14、1.
15、10
16、1
三、解下列各题(本大题共8小题,共72分)
17、 (1)y=-![]() x+1(2)第一、二、四象限(3)
x+1(2)第一、二、四象限(3) ![]()
18、(1)y=6x-2;(2)a<b.
19、见解析
20、(1)20%;(2)详见解析;(3)96.
21、证明见解析.
22、(1)![]() ;(2)平行四边形
;(2)平行四边形![]() 的周长是
的周长是![]() .
.
23、(1)不变,![]() ;(2)正方形ADEF的边长为
;(2)正方形ADEF的边长为![]() 或
或![]() 或
或![]() .
.
24、(1)![]() (2)
(2)![]()
相关试卷
这是一份广东省广州市广州外国语学校2023-2024学年八上数学期末学业质量监测模拟试题含答案,共6页。试卷主要包含了考生要认真填写考场号和座位序号,如图,在△ABC中,已知,下列四个式子中能因式分解的是,下列各式计算正确的是等内容,欢迎下载使用。
这是一份2023-2024学年重庆市西南大附中八上数学期末学业质量监测模拟试题含答案,共9页。试卷主要包含了下列坐标点在第四象限的是,下列各因式分解中,结论正确的是,下列从左到右的变形等内容,欢迎下载使用。
这是一份2023-2024学年广东省广州市广大附中八上数学期末学业质量监测模拟试题含答案,共8页。试卷主要包含了下列说法错误的是等内容,欢迎下载使用。












