


广东省惠州市名校2022-2023学年数学七年级第二学期期末考试模拟试题含答案
展开
这是一份广东省惠州市名校2022-2023学年数学七年级第二学期期末考试模拟试题含答案,共7页。试卷主要包含了若有意义,则的取值范围是,对于抛物线y=﹣,下列等式成立的是等内容,欢迎下载使用。
广东省惠州市名校2022-2023学年数学七年级第二学期期末考试模拟试题(时间:120分钟 分数:120分) 学校_______ 年级_______ 姓名_______ 考生须知:1.全卷分选择题和非选择题两部分,全部在答题纸上作答。选择题必须用2B铅笔填涂;非选择题的答案必须用黑色字迹的钢笔或答字笔写在“答题纸”相应位置上。2.请用黑色字迹的钢笔或答字笔在“答题纸”上先填写姓名和准考证号。3.保持卡面清洁,不要折叠,不要弄破、弄皱,在草稿纸、试题卷上答题无效。 一、选择题(每小题3分,共30分)1.计算(![]() )2的结果是( )A.-2 B.2 C.±2 D.42.下列命题①同旁内角互补,两直线平行;②全等三角形的周长相等;③直角都相等;④等边对等角.它们的逆命题是真命题的个数是( )A.1个 B.2个 C.3个 D.4个3.如图,等边三角形ABC中,AD⊥BC,垂足为D,点E在线段AD上,∠EBC=45°,则∠ACE等于( )
)2的结果是( )A.-2 B.2 C.±2 D.42.下列命题①同旁内角互补,两直线平行;②全等三角形的周长相等;③直角都相等;④等边对等角.它们的逆命题是真命题的个数是( )A.1个 B.2个 C.3个 D.4个3.如图,等边三角形ABC中,AD⊥BC,垂足为D,点E在线段AD上,∠EBC=45°,则∠ACE等于( )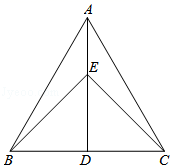 A.15° B.30° C.45° D.60°4.若
A.15° B.30° C.45° D.60°4.若![]() 有意义,则
有意义,则![]() 的取值范围是( )A.
的取值范围是( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 且
且![]() 5.对于抛物线y=﹣(x+2)2﹣1,下列说法错误的是( )A.开口向下B.对称轴是直线x=﹣2C.x>﹣2时,y随x的增大而增大D.x=﹣2,函数有最大值y=﹣16.下列等式成立的是( )A.
5.对于抛物线y=﹣(x+2)2﹣1,下列说法错误的是( )A.开口向下B.对称轴是直线x=﹣2C.x>﹣2时,y随x的增大而增大D.x=﹣2,函数有最大值y=﹣16.下列等式成立的是( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 7.如图圆柱的底面周长是
7.如图圆柱的底面周长是![]() ,圆柱的高为
,圆柱的高为![]() ,
,![]() 为圆柱上底面的直径,一只蚂蚁如果沿着圆柱的侧面从下底面点
为圆柱上底面的直径,一只蚂蚁如果沿着圆柱的侧面从下底面点![]() 处爬到上底面点
处爬到上底面点![]() 处,那么它爬行的最短路程为( )
处,那么它爬行的最短路程为( ) 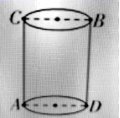 A.
A.![]() B.
B.![]() C.
C.![]() D.
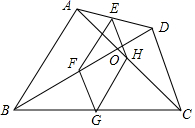
D.![]() 8.如图,四边形ABCD中,对角线相交于点O,E、F、G、H分别是AD、BD、BC、AC的中点,要使四边形EFGH是矩形,则四边形ABCD需要满足的条件是
8.如图,四边形ABCD中,对角线相交于点O,E、F、G、H分别是AD、BD、BC、AC的中点,要使四边形EFGH是矩形,则四边形ABCD需要满足的条件是![]()
![]()
 A.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 9.在平面直角坐标系中,点
9.在平面直角坐标系中,点![]() 向上平移2个单位后的对应点
向上平移2个单位后的对应点![]() 的坐标为( )A.
的坐标为( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 10.某班数学兴趣小组
10.某班数学兴趣小组![]() 位同学的一次数学测验成绩为
位同学的一次数学测验成绩为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() (单位:分),经过计算这组数据的方差为
(单位:分),经过计算这组数据的方差为![]() ,小李和小明同学成绩均为
,小李和小明同学成绩均为![]() 分,若该组加入这两位同学的成绩则( )A.平均数变小 B.方差变大 C.方差变小 D.方差不变二、填空题(本大题共有6小题,每小题3分,共18分)11.两条对角线______的四边形是平行四边形.12.如图,沿折痕AE折叠矩形ABCD的一边,使点D落在BC边上一点F处.若AB=8,且△ABF的面积为24,则EC的长为__.
分,若该组加入这两位同学的成绩则( )A.平均数变小 B.方差变大 C.方差变小 D.方差不变二、填空题(本大题共有6小题,每小题3分,共18分)11.两条对角线______的四边形是平行四边形.12.如图,沿折痕AE折叠矩形ABCD的一边,使点D落在BC边上一点F处.若AB=8,且△ABF的面积为24,则EC的长为__.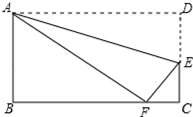 13.当x=______时,分式
13.当x=______时,分式![]() 的值是1.14.如图,在△ABC中,AB=4,BC=6,∠B=60°,将△ABC沿射线BC方向平移2个单位后得到△DEF,连接DC,则DC的长为________________.
的值是1.14.如图,在△ABC中,AB=4,BC=6,∠B=60°,将△ABC沿射线BC方向平移2个单位后得到△DEF,连接DC,则DC的长为________________.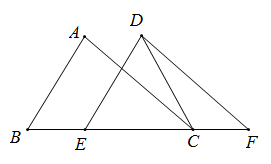 15.如图是由6个形状大小完全相同菱形组成的网格,若菱形的边长为1,一个内角(∠O)为60°,△ABC的各顶点都在格点上,则BC边上的高为______.
15.如图是由6个形状大小完全相同菱形组成的网格,若菱形的边长为1,一个内角(∠O)为60°,△ABC的各顶点都在格点上,则BC边上的高为______.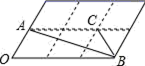 16.如图,在Rt△ABC中,∠A=30°,斜边AB=12,CD⊥AB于D,则AD=_____________.
16.如图,在Rt△ABC中,∠A=30°,斜边AB=12,CD⊥AB于D,则AD=_____________.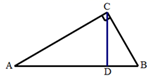 三、解下列各题(本大题共8小题,共72分)17.(8分)某地区2015年投入教育经费2900万元,2017年投入教育经费3509万元.(1)求2015年至2017年该地区投入教育经费的年平均增长率;(2)按照义务教育法规定,教育经费的投入不低于国民生产总值的百分之四,结合该地区国民生产总值的情况,该地区到2019年需投入教育经费4250万元.如果按(1)中教育经费投入的增长率,到2019年该地区投入的教育经费是否能达到4250万元?请说明理由. 18.(8分)计算或解不等式组:(1)计算
三、解下列各题(本大题共8小题,共72分)17.(8分)某地区2015年投入教育经费2900万元,2017年投入教育经费3509万元.(1)求2015年至2017年该地区投入教育经费的年平均增长率;(2)按照义务教育法规定,教育经费的投入不低于国民生产总值的百分之四,结合该地区国民生产总值的情况,该地区到2019年需投入教育经费4250万元.如果按(1)中教育经费投入的增长率,到2019年该地区投入的教育经费是否能达到4250万元?请说明理由. 18.(8分)计算或解不等式组:(1)计算![]() .(2)解不等式组
.(2)解不等式组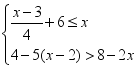 19.(8分)如图,矩形ABCD中,点E在BC上,AE=CE,试分别在下列两个图中按要求使用无刻度的直尺画图.(1)在图1中,画出∠DAE的平分线;(2)在图2中,画出∠AEC的平分线.
19.(8分)如图,矩形ABCD中,点E在BC上,AE=CE,试分别在下列两个图中按要求使用无刻度的直尺画图.(1)在图1中,画出∠DAE的平分线;(2)在图2中,画出∠AEC的平分线.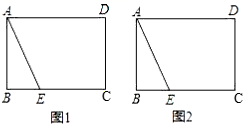 20.(8分)为了庆祝新中国成立70周年,某校组织八年级全体学生参加“恰同学少年,忆峥嵘岁月”新中国成立70周年知识竞赛活动.将随机抽取的部分学生成绩进行整理后分成5组,50~60分(
20.(8分)为了庆祝新中国成立70周年,某校组织八年级全体学生参加“恰同学少年,忆峥嵘岁月”新中国成立70周年知识竞赛活动.将随机抽取的部分学生成绩进行整理后分成5组,50~60分(![]() )的小组称为“学童”组,60~70分(
)的小组称为“学童”组,60~70分(![]() )的小组称为“秀才”组,70~80分(
)的小组称为“秀才”组,70~80分(![]() )的小组称为“举人”组,80~90分(
)的小组称为“举人”组,80~90分(![]() )的小组称为“进士”组,90~100分(
)的小组称为“进士”组,90~100分(![]() )的小组称为“翰林”组,并绘制了不完整的频数分布直方图如下,请结合提供的信息解答下列问题:
)的小组称为“翰林”组,并绘制了不完整的频数分布直方图如下,请结合提供的信息解答下列问题: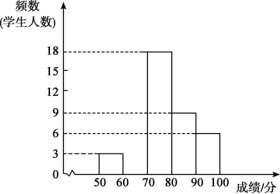 (1)若“翰林”组成绩的频率是12.5%,请补全频数分布直方图;(2)在此次比赛中,抽取学生的成绩的中位数在 组;(3)学校决定对成绩在70~100分(
(1)若“翰林”组成绩的频率是12.5%,请补全频数分布直方图;(2)在此次比赛中,抽取学生的成绩的中位数在 组;(3)学校决定对成绩在70~100分(![]() )的学生进行奖励,若八年级共有336名学生,请通过计算说明,大约有多少名学生获奖? 21.(8分)如图1,在正方形ABCD中,点E、F分别是边BC、CD上的点,且CE=CF,连接AE,AF,取AE的中点M,EF的中点N,连接BM,MN.
)的学生进行奖励,若八年级共有336名学生,请通过计算说明,大约有多少名学生获奖? 21.(8分)如图1,在正方形ABCD中,点E、F分别是边BC、CD上的点,且CE=CF,连接AE,AF,取AE的中点M,EF的中点N,连接BM,MN.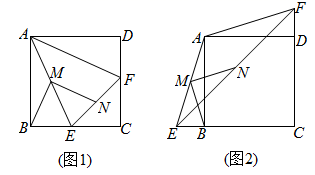 (1)请判断线段BM与MN的数量关系和位置关系,并予以证明.(2)如图2,若点E在CB的延长线上,点F在CD的延长线上,其他条件不变,(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由. 22.(10分)已知直线y=kx+b经过点A(﹣20,1)、B(10,20)两点.(1)求直线y=kx+b的表达式;(2)当x取何值时,y>1. 23.(10分)在平行四边形ABCD中,∠BAD的平分线交线段BC于点E,交线段DC的延长线于点F,以EC、CF为邻边作平行四边形ECFG.(1)如图1,证明平行四边形ECFG为菱形;(2)如图2,若∠ABC=90°,M是EF的中点,求∠BDM的度数;(3)如图3,若∠ABC=120°,请直接写出∠BDG的度数.
(1)请判断线段BM与MN的数量关系和位置关系,并予以证明.(2)如图2,若点E在CB的延长线上,点F在CD的延长线上,其他条件不变,(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由. 22.(10分)已知直线y=kx+b经过点A(﹣20,1)、B(10,20)两点.(1)求直线y=kx+b的表达式;(2)当x取何值时,y>1. 23.(10分)在平行四边形ABCD中,∠BAD的平分线交线段BC于点E,交线段DC的延长线于点F,以EC、CF为邻边作平行四边形ECFG.(1)如图1,证明平行四边形ECFG为菱形;(2)如图2,若∠ABC=90°,M是EF的中点,求∠BDM的度数;(3)如图3,若∠ABC=120°,请直接写出∠BDG的度数.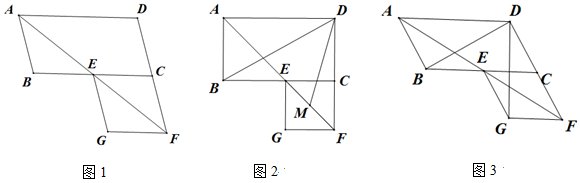 24.(12分)求不等式(2x﹣1)(x+1)>0的解集.解:根据“同号两数相乘,积为正”可得:①
24.(12分)求不等式(2x﹣1)(x+1)>0的解集.解:根据“同号两数相乘,积为正”可得:①![]() 或 ②
或 ②![]() .解①得x>
.解①得x>![]() ;解②得x<﹣1.∴不等式的解集为x>
;解②得x<﹣1.∴不等式的解集为x>![]() 或x<﹣1.请你仿照上述方法解决下列问题:(1)求不等式(2x﹣1)(x+1)<0的解集.(2)求不等式
或x<﹣1.请你仿照上述方法解决下列问题:(1)求不等式(2x﹣1)(x+1)<0的解集.(2)求不等式![]() ≥0的解集. 参考答案 一、选择题(每小题3分,共30分)1、B2、B3、A4、B5、C6、B7、C8、B9、B10、C 二、填空题(本大题共有6小题,每小题3分,共18分)11、互相平分12、213、114、1.15、
≥0的解集. 参考答案 一、选择题(每小题3分,共30分)1、B2、B3、A4、B5、C6、B7、C8、B9、B10、C 二、填空题(本大题共有6小题,每小题3分,共18分)11、互相平分12、213、114、1.15、![]() 16、1 三、解下列各题(本大题共8小题,共72分)17、 (1)10%(2)不能.18、(1)
16、1 三、解下列各题(本大题共8小题,共72分)17、 (1)10%(2)不能.18、(1)![]() ;(2)不等式组无解.19、作图见解析20、(1)详见解析;(2)70~80或“举人”;(3)231.21、(1)BM=MN,BM⊥MN,证明见解析;(2)仍然成立,证明见解析22、(1)y=
;(2)不等式组无解.19、作图见解析20、(1)详见解析;(2)70~80或“举人”;(3)231.21、(1)BM=MN,BM⊥MN,证明见解析;(2)仍然成立,证明见解析22、(1)y=![]() x+11;(2)x>﹣20时,y>1.23、(1)证明见解析;(2)∠BDM的度数为45°;(3)∠BDG的度数为60°.24、(1)﹣1<x<
x+11;(2)x>﹣20时,y>1.23、(1)证明见解析;(2)∠BDM的度数为45°;(3)∠BDG的度数为60°.24、(1)﹣1<x<![]() ;(2)x≥1或x<﹣2.
;(2)x≥1或x<﹣2.
相关试卷
这是一份广东省惠州市名校2023-2024学年数学八上期末联考模拟试题含答案,共7页。试卷主要包含了考生必须保证答题卡的整洁,下列标志中属于轴对称图形的是等内容,欢迎下载使用。
这是一份广东省惠州市名校2022-2023学年七下数学期末达标检测模拟试题含答案,共6页。试卷主要包含了下列二次根式中,不能与合并的是等内容,欢迎下载使用。
这是一份广东省惠州市惠东燕岭学校2022-2023学年数学七年级第二学期期末联考模拟试题含答案,共7页。试卷主要包含了已知点P等内容,欢迎下载使用。








