广东省深圳市深圳实验学校初中部联考2022-2023学年七年级数学第二学期期末调研模拟试题含答案

这是一份广东省深圳市深圳实验学校初中部联考2022-2023学年七年级数学第二学期期末调研模拟试题含答案，共7页。试卷主要包含了考生必须保证答题卡的整洁，要使式子有意义，则的取值范围是，如果不等式等内容，欢迎下载使用。
广东省深圳市深圳实验学校初中部联考2022-2023学年七年级数学第二学期期末调研模拟试题（时间：120分钟             分数：120分） 学校_______            年级_______        姓名_______ 考生请注意：1．答题前请将考场、试室号、座位号、考生号、姓名写在试卷密封线内，不得在试卷上作任何标记。2．第一部分选择题每小题选出答案后，需将答案写在试卷指定的括号内，第二部分非选择题答案写在试卷题目指定的位置上。3．考生必须保证答题卡的整洁。考试结束后，请将本试卷和答题卡一并交回。 一、选择题(每小题3分,共30分)1．若a+c=b，那么方程ax2+bx+c=0（a≠0）必有一根是（　　）A．1    B．﹣1    C．±1    D．02．矩形的对角线一定具有的性质是（　　）A．互相垂直 B．互相垂直且相等C．相等 D．互相垂直平分3．若无解，则m的值是（　　）A．3 B．﹣3 C．﹣2 D．24．如图，平行四边形ABCD中，于点E，CE的垂真平分线MV分别交AD、BC于M、N，交CE于O，连接CM、EM，下列结论：（1）（2）（3）（4）·其中正确的个数有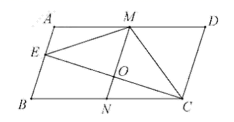（    ）A．1个 B．2个 C．3个 D．4个5．要使式子有意义，则的取值范围是（ ）A． B． C． D．6．下列各组数中能作为直角三角形的三边长的是（　　）．A．1，，1 B．2，3，4 C．4，5，6 D．8，13，57．禽流感病毒的形状一般为球形，直径大约为0.000000102m，该直径用科学记数法表示为（　　）A．1.02×10﹣7m B．10.2×10﹣7m C．1.02×10﹣6m D．1.0×10﹣8m8．如果不等式（a+1）x＜a+1的解集为x＞1，那么a的取值范围是（　　）A．a＜1 B．a＜﹣1 C．a＞1 D．a＞﹣19．把一张正方形纸片按如图所示的方法对折两次后剪去两个角，那么打开以后的形状是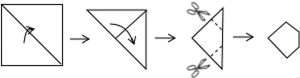（　　）A．六边形 B．八边形 C．十二边形 D．十六边形10．二次根式在实数范围内有意义，则a的取值范围是（　　）A．a≤﹣2 B．a≥﹣2 C．a＜﹣2 D．a＞﹣2二、填空题(本大题共有6小题，每小题3分，共18分)11．一个有进水管与出水管的容器，从某时刻开始的4分钟内只进水不出水，在随后的若干分内既进水又出水，之后只出水不进水．每分钟的进水量和出水量是两个常数，容器内的水量y（单位：升）与时间x（单位：分）之间的关系如图．则a= 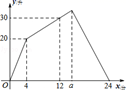         ．12．若关于的分式方程有增根，则的值为__________．13．若＜0，则代数式可化简为_____.14．使分式的值为0，这时x=_____．15．已知等腰三角形的两条边长分别是3cm、7cm，那么这个等腰三角形的周长是________cm．16．如图，Rt△ABC中，∠C＝90°，AC＝BC，∠BAC的平分线AD交BC于点D，分别过点A作AE∥BC，过点B作BE∥AD，AE与BE相交于点E．若CD＝2，则四边形ADBE的面积是_____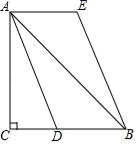．三、解下列各题(本大题共8小题，共72分)17．（8分）（1） [探索发现]正方形中,是对角线上的一个动点(与点不重合),过点作交线段于点．求证: 小玲想到的思路是:过点作于点于点,通过证明得到．请按小玲的思路写出证明过程（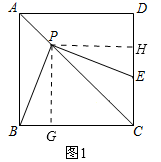2）[应用拓展]如图2,在的条件下，设正方形的边长为,过点作交于点．求的长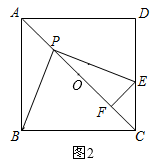．   18．（8分）直线y=x-6与x轴、y轴分别交于点A、B，点E从B点，出发以每秒1个单位的速度沿线段BO向O点移动（与B、O点不重合），过E作EF//AB，交x轴于F．将四边形ABEF沿EF折叠，得到四边形DCEF，设点E的运动时间为t秒．（1）①直线y=x-6与坐标轴交点坐标是A(_____，______)，B(______，_____)；②画出t=2时，四边形ABEF沿EF折叠后的图形（不写画法）；（2）若CD交y轴于H点，求证：四边形DHEF为平行四边形；并求t为何值时，四边形DHEF为菱形（计算结果不需化简）；（3）连接AD，BC四边形ABCD是什么图形，并求t为何值时，四边形ABCD的面积为36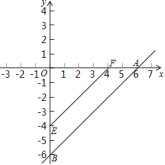？   19．（8分）如图，已知反比例函数y1＝的图象与一次函数：y2＝ax+b的图象相交于点A（1，4）、B（m，﹣2）（1）求出反比例函数和一次函数的关系式；（2）观察图象，直按写出使得y1＜y2成立的自变量x的取值范围；（3）如果点C是x轴上的点，且△ABC的面积面积为6，求点C的坐标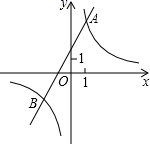．   20．（8分）    写出同时具备下列两个条件的一次函数关系式_____．（写出一个即可）（1）y随x的增大而减小；（2）图象经过点（1，﹣2）．   21．（8分）如图，在中，，、分别是、的中点，延长到，使得，连接、.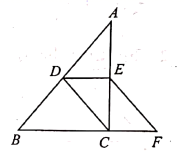（1）求证：四边形为平行四边形；（2）若四边形的周长是32，，求的面积；（3）在（2）的条件下，求点到直线的距离.   22．（10分）如图所示，正方形ABCD的边长为4，AD∥y轴，D(1，－1)．(1)写出A，B，C三个顶点的坐标；(2)写出BC的中点P的坐标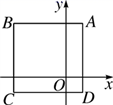．   23．（10分）如图，已知等边△ABC，点D在直线BC上，连接AD，作∠ADN=60°，直线DN交射线AB于点E，过点C作CF∥AB交直线DN于点F.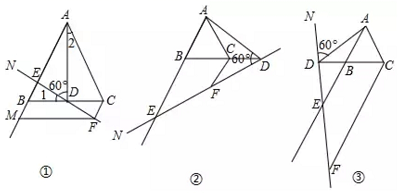（1）当点D在线段BC上，∠NDB为锐角时，如图①.①判断∠1与∠2的大小关系，并说明理由；②过点F作FM∥BC交射线AB于点M，求证：CF+BE=CD；（2）①当点D在线段BC的延长线上，∠NDB为锐角时，如图②，请直接写出线段CF，BE，CD之间的数量关系；②当点D在线段CB的延长线上，∠NDB为钝角或直角时，如图③，请直接写出线段CF，BE，CD之间的数量关系.   24．（12分）已知：如图，四边形ABCD四条边上的中点分别为E、F、G、H，顺次连接EF、FG、GH、HE，得到四边形EFGH（即四边形ABCD的中点四边形）．（1）四边形EFGH的形状是　   　，证明你的结论；（2）当四边形ABCD的对角线满足　   　条件时，四边形EFGH是矩形；（3）你学过的哪种特殊四边形的中点四边形是矩形？　   　．（不证明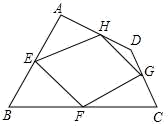）   参考答案 一、选择题(每小题3分,共30分)1、B2、C3、D4、C5、D6、A7、A8、B9、B10、B 二、填空题(本大题共有6小题，每小题3分，共18分)11、1．12、13、14、115、116、 三、解下列各题(本大题共8小题，共72分)17、（1）详见解析；（2）18、（1）①6，0，0，-6；②见详解；（2）证明见详解，当时，四边形DHEF为菱形；（3）四边形ABCD是矩形，当时，四边形ABCD的面积为1．19、（1）反比例函数的解析式为y1＝，一次函数的解析式为  y1＝1x+1；（1）﹣1＜x＜0或x＞1；（3）C的坐标（1，0）或（﹣3，0）．20、y=－x－121、（1）见解析；（2）96；（3）4.822、（1）A（1，3），B（-3，3），C（-3，-1）；（2）P的坐标（-3，1）．23、（1）①∠1=∠2，理由见解析，②证明见解析；（2）①BE=CD+CF，②CF=CD+BE．24、（1）平行四边形；（2）互相垂直；（3）菱形.