


云南省峨山县大龙潭中学2022-2023学年七年级数学第二学期期末学业水平测试模拟试题含答案
展开
这是一份云南省峨山县大龙潭中学2022-2023学年七年级数学第二学期期末学业水平测试模拟试题含答案,共7页。试卷主要包含了考生要认真填写考场号和座位序号,一次函数的图象可能是等内容,欢迎下载使用。
云南省峨山县大龙潭中学2022-2023学年七年级数学第二学期期末学业水平测试模拟试题(时间:120分钟 分数:120分) 学校_______ 年级_______ 姓名_______ 注意事项1.考生要认真填写考场号和座位序号。2.试题所有答案必须填涂或书写在答题卡上,在试卷上作答无效。第一部分必须用2B 铅笔作答;第二部分必须用黑色字迹的签字笔作答。3.考试结束后,考生须将试卷和答题卡放在桌面上,待监考员收回。 一、选择题(每小题3分,共30分)1.下列各式正确的是( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 2.一次信息技术模拟测试后,数学兴趣小组的同学随机统计了九年级20名学生的成绩
2.一次信息技术模拟测试后,数学兴趣小组的同学随机统计了九年级20名学生的成绩![]() 记录如下:有5人得10分,6人得9分,5人得8分,4人得7分
记录如下:有5人得10分,6人得9分,5人得8分,4人得7分![]() 这20名学生成绩的中位数和众数分别是
这20名学生成绩的中位数和众数分别是![]()
![]() A.10分,9分 B.9分,10分 C.9分,9分 D.
A.10分,9分 B.9分,10分 C.9分,9分 D.![]() 分,9分3.如图,将一个含
分,9分3.如图,将一个含![]() 角的直角三角板
角的直角三角板![]() 绕点
绕点![]() 旋转,得点
旋转,得点![]() ,
,![]() ,
,![]() ,在同一条直线上,则旋转角
,在同一条直线上,则旋转角![]() 的度数是( )
的度数是( )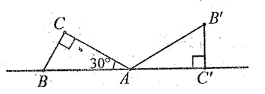 A.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 4.如果5x=6y,那么下列结论正确的是( )A.
4.如果5x=6y,那么下列结论正确的是( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 5.如图,在RtΔABC中,∠C=90°,BC=6,AC=8,则AB的长度为( )
5.如图,在RtΔABC中,∠C=90°,BC=6,AC=8,则AB的长度为( ) A.7 B.8 C.9 D.106.代数式
A.7 B.8 C.9 D.106.代数式![]() 在实数范围内有意义,实数
在实数范围内有意义,实数![]() 取值范围是( )A.
取值范围是( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 7.一次函数
7.一次函数![]() 的图象可能是( )A.
的图象可能是( )A.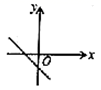 B.
B. C.
C. D.
D. 8.如图,把一个边长为1的正方形放在数轴上,以正方形的对角线为半径画弧交数轴于点A,则点A对应的数为( ).
8.如图,把一个边长为1的正方形放在数轴上,以正方形的对角线为半径画弧交数轴于点A,则点A对应的数为( ).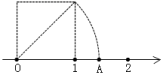 A.
A.![]() B.1.5 C.
B.1.5 C.![]() D.1.79.已知直角三角形的两直角边长分别为5和12,则此直角三角形斜边上的中线长为()A.
D.1.79.已知直角三角形的两直角边长分别为5和12,则此直角三角形斜边上的中线长为()A.![]() B.6 C.13 D.
B.6 C.13 D.![]() 10.在2014年的体育中考中,某校6名学生的体育成绩统计如图,则这组数据的众数、中位数、方差依次是( )
10.在2014年的体育中考中,某校6名学生的体育成绩统计如图,则这组数据的众数、中位数、方差依次是( )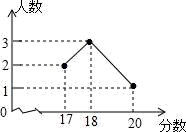 A.18,18,1 B.18,17.5,3 C.18,18,3 D.18,17.5,1二、填空题(本大题共有6小题,每小题3分,共18分)11.如图,已知在△ABC中,AB=AC.以AB为直径作半圆O,交BC于点D. 若∠BAC=40°,则AD弧的度数是___度.
A.18,18,1 B.18,17.5,3 C.18,18,3 D.18,17.5,1二、填空题(本大题共有6小题,每小题3分,共18分)11.如图,已知在△ABC中,AB=AC.以AB为直径作半圆O,交BC于点D. 若∠BAC=40°,则AD弧的度数是___度.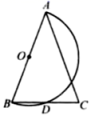 12.若关于
12.若关于![]() 有增根,则
有增根,则![]() _____;13.数据﹣2,﹣1,0,3,5的方差是 .14.因式分解:
_____;13.数据﹣2,﹣1,0,3,5的方差是 .14.因式分解:![]() ________.15.如图,在平行四边形
________.15.如图,在平行四边形![]() 中,对角线
中,对角线![]() 、
、![]() 相交于点
相交于点![]() ,若
,若![]() ,
,![]() ,sin∠BDC=
,sin∠BDC=![]() ,则平行四边形
,则平行四边形![]() 的面积是__________.
的面积是__________. 16.如图,矩形ABCD中,
16.如图,矩形ABCD中,![]() ,
,![]() ,CB在数轴上,点C表示的数是
,CB在数轴上,点C表示的数是![]() ,若以点C为圆心,对角线CA的长为半径作弧交数轴的正半轴于点P,则点P表示的数是______.
,若以点C为圆心,对角线CA的长为半径作弧交数轴的正半轴于点P,则点P表示的数是______. 三、解下列各题(本大题共8小题,共72分)17.(8分)已知矩形0ABC在平面直角坐标系内的位置如图所示,点0为坐标原点,点A的坐标为(10,0),点B的坐标为(10,8),点Q为线段AC上-点,其坐标为(5,n).
三、解下列各题(本大题共8小题,共72分)17.(8分)已知矩形0ABC在平面直角坐标系内的位置如图所示,点0为坐标原点,点A的坐标为(10,0),点B的坐标为(10,8),点Q为线段AC上-点,其坐标为(5,n). (1)求直线AC的表达式(2)如图,若点P为坐标轴上-动点,动点P沿折线AO→0C的路径以每秒1个单位长度的速度运动,到达C处停止求Δ0PQ的面积S与点P的运动时间t(秒)的函数关系式.(3)若点P为坐标平面内任意-.点,是否存在这样的点P,使以0,C,P,Q为顶点的四边形为平行四边形?若存在,请直接写出点P的坐标,若不存在,请说明理由. 18.(8分)某校300名学生参加植树活动,要求每人植4~7棵,活动结束后随机抽查了20名学生每人的植树量,并分为四种类型,A:4棵;B:5棵;C:6棵;D:7棵.将各类的人数绘制成扇形图(如图1)和条形图(如图2),经确认扇形图是正确的,而条形图尚有一处错误.回答下列问题:(1)条形图中存在错误的类型是 ,人数应该为 人;(2)写出这20名学生每人植树量的众数 棵,中位数 棵;(3)估计这300名学生共植树 棵.
(1)求直线AC的表达式(2)如图,若点P为坐标轴上-动点,动点P沿折线AO→0C的路径以每秒1个单位长度的速度运动,到达C处停止求Δ0PQ的面积S与点P的运动时间t(秒)的函数关系式.(3)若点P为坐标平面内任意-.点,是否存在这样的点P,使以0,C,P,Q为顶点的四边形为平行四边形?若存在,请直接写出点P的坐标,若不存在,请说明理由. 18.(8分)某校300名学生参加植树活动,要求每人植4~7棵,活动结束后随机抽查了20名学生每人的植树量,并分为四种类型,A:4棵;B:5棵;C:6棵;D:7棵.将各类的人数绘制成扇形图(如图1)和条形图(如图2),经确认扇形图是正确的,而条形图尚有一处错误.回答下列问题:(1)条形图中存在错误的类型是 ,人数应该为 人;(2)写出这20名学生每人植树量的众数 棵,中位数 棵;(3)估计这300名学生共植树 棵. 19.(8分)如图,在
19.(8分)如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,求
,求![]() 的长.
的长.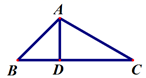 20.(8分)如图,在Rt△ABC中,∠C=90°,△ACD沿AD折叠,使得点C落在斜边AB上的点E处.
20.(8分)如图,在Rt△ABC中,∠C=90°,△ACD沿AD折叠,使得点C落在斜边AB上的点E处. (1)求证:△BDE∽△BAC;(2)已知AC=6,BC=8,求线段AD的长度. 21.(8分)如图,在四边形OABC中,OA∥BC,∠OAB=90°,O为原点,点C的坐标为(2,8),点A的坐标为(26,0),点D从点B出发,以每秒1个单位长度的速度沿BC向点C运动,点E同时从点O出发,以每秒3个单位长度的速度沿折线OAB运动,当点E达到点B时,点D也停止运动,从运动开始,设D(E)点运动的时间为t秒.(1)当t为何值时,四边形ABDE是矩形;(2)当t为何值时,DE=CO?(3)连接AD,记△ADE的面积为S,求S与t的函数关系式.
(1)求证:△BDE∽△BAC;(2)已知AC=6,BC=8,求线段AD的长度. 21.(8分)如图,在四边形OABC中,OA∥BC,∠OAB=90°,O为原点,点C的坐标为(2,8),点A的坐标为(26,0),点D从点B出发,以每秒1个单位长度的速度沿BC向点C运动,点E同时从点O出发,以每秒3个单位长度的速度沿折线OAB运动,当点E达到点B时,点D也停止运动,从运动开始,设D(E)点运动的时间为t秒.(1)当t为何值时,四边形ABDE是矩形;(2)当t为何值时,DE=CO?(3)连接AD,记△ADE的面积为S,求S与t的函数关系式. 22.(10分)八年级下册教材第69页习题14:四边形ABCD是正方形,点E是边BC的中点,∠AEF=90°,且EF交正方形外角的平分线CF于点F.求证:AE=EF.这道题对大多数同学来说,印象深刻数学课代表在做完这题后,她把这题稍作改动,如图,四边形ABCD是正方形,点E是边BC的三等分点,∠AEF=90°,且EF交正方形外角的平分线CF于点F,那么AE=EF还成立吗?如果成立,给予证明,如果不成立,请说明理由.
22.(10分)八年级下册教材第69页习题14:四边形ABCD是正方形,点E是边BC的中点,∠AEF=90°,且EF交正方形外角的平分线CF于点F.求证:AE=EF.这道题对大多数同学来说,印象深刻数学课代表在做完这题后,她把这题稍作改动,如图,四边形ABCD是正方形,点E是边BC的三等分点,∠AEF=90°,且EF交正方形外角的平分线CF于点F,那么AE=EF还成立吗?如果成立,给予证明,如果不成立,请说明理由. 23.(10分)如图,△ABC全等于△DEF,点B,E,C,F在同一直线,连接AD,求证:四边形ABED是平行四边形.
23.(10分)如图,△ABC全等于△DEF,点B,E,C,F在同一直线,连接AD,求证:四边形ABED是平行四边形.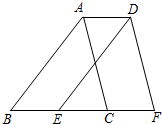 24.(12分)某公司招聘人才,对应聘者分别进行了阅读能力、思维能力和表达能力三项测试,其中甲、乙两人的测试成绩(百分制)如下表:(单位:分)应聘者阅读能力思维能力表达能力甲859080乙958095(1)若根据三项测试的平均成绩在甲、乙两人中录用一人,那么谁将被录用?(2)若将阅读能力、思维能力和表达能力三项测试得分按1:3:1的比确定每人的最后成绩,谁将被录用? 参考答案 一、选择题(每小题3分,共30分)1、C2、C3、D4、A5、D6、A7、A8、A9、D10、A 二、填空题(本大题共有6小题,每小题3分,共18分)11、14012、113、
24.(12分)某公司招聘人才,对应聘者分别进行了阅读能力、思维能力和表达能力三项测试,其中甲、乙两人的测试成绩(百分制)如下表:(单位:分)应聘者阅读能力思维能力表达能力甲859080乙958095(1)若根据三项测试的平均成绩在甲、乙两人中录用一人,那么谁将被录用?(2)若将阅读能力、思维能力和表达能力三项测试得分按1:3:1的比确定每人的最后成绩,谁将被录用? 参考答案 一、选择题(每小题3分,共30分)1、C2、C3、D4、A5、D6、A7、A8、A9、D10、A 二、填空题(本大题共有6小题,每小题3分,共18分)11、14012、113、![]() .14、
.14、![]() 15、116、
15、116、![]() 三、解下列各题(本大题共8小题,共72分)17、 (1)
三、解下列各题(本大题共8小题,共72分)17、 (1) ![]() ; (2) 当点P在A0上运动时,S=2t+20 ,当点P在0C上运动时,S
; (2) 当点P在A0上运动时,S=2t+20 ,当点P在0C上运动时,S ![]() (10≤t≤18) ;(3)点P的坐标为(5,12),(5,-4),(-5,4)18、(1)D,2;(2)5, 5;(3)1.19、
(10≤t≤18) ;(3)点P的坐标为(5,12),(5,-4),(-5,4)18、(1)D,2;(2)5, 5;(3)1.19、![]() 20、(1)证明见试题解析;(2)
20、(1)证明见试题解析;(2)![]() .21、 (1)t=
.21、 (1)t=![]() ;(2)t=6;(3)S=
;(2)t=6;(3)S=![]() t2﹣13t.22、成立,理由见解析.23、见解析24、(1)乙将被录用;(2)甲将被录用
t2﹣13t.22、成立,理由见解析.23、见解析24、(1)乙将被录用;(2)甲将被录用
相关试卷
这是一份2023-2024学年云南省峨山县大龙潭中学九上数学期末统考试题含答案,共8页。
这是一份云南省峨山县大龙潭中学2023-2024学年八年级数学第一学期期末统考模拟试题含答案,共6页。试卷主要包含了考生必须保证答题卡的整洁,下列图案中,是轴对称图形的有个等内容,欢迎下载使用。
这是一份宁夏大附属中学2022-2023学年数学七年级第二学期期末学业水平测试模拟试题含答案,共7页。试卷主要包含了在平面直角坐标系中,将点P,如图,有两个可以自由转动的转盘等内容,欢迎下载使用。








