内蒙古兴安盟地区两旗一县2022-2023学年七下数学期末学业水平测试模拟试题含答案

这是一份内蒙古兴安盟地区两旗一县2022-2023学年七下数学期末学业水平测试模拟试题含答案，共7页。试卷主要包含了考生必须保证答题卡的整洁，化简的结果是等内容，欢迎下载使用。
内蒙古兴安盟地区两旗一县2022-2023学年七下数学期末学业水平测试模拟试题（时间：120分钟             分数：120分） 学校_______            年级_______        姓名_______ 考生请注意：1．答题前请将考场、试室号、座位号、考生号、姓名写在试卷密封线内，不得在试卷上作任何标记。2．第一部分选择题每小题选出答案后，需将答案写在试卷指定的括号内，第二部分非选择题答案写在试卷题目指定的位置上。3．考生必须保证答题卡的整洁。考试结束后，请将本试卷和答题卡一并交回。 一、选择题(每小题3分,共30分)1．在“爱我莒州”中学生演讲比赛中，五位评委分别给甲、乙两位选手的评分如下：甲8、7、9、8、8； 乙：7、9、6、9、9，则下列说法中错误的是（    ）A．甲得分的众数是8 B．乙得分的众数是9C．甲得分的中位数是9 D．乙得分的中位数是92．某多边形的每个内角均为120°，则此多边形的边数为（     ）.A．5    B．6    C．7    D．83．如图，在△ABC中，∠B＝45°，∠ACB＝60°，AB＝16，AD⊥BC，垂足为D，∠ACB的平分线交AD于点E，则AE的长为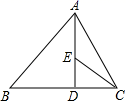（　　）A． B．4 C． D．64．下面哪个点在函数y=2x+4的图象上（　　）A．（2，1） B．（-2，1） C．（2，0） D．（-2，0）5． “厉害了，华为!”2019 年 1 月 7 日，华为宣布推出业界最高性能 ABM- based 处理器—鲲鹏 920.据了解，该处理器采用 7 纳米制造工艺，已知 1 纳米=0.000 000 001 米，则 7 纳米用科学记数法表示为 (          )A．7×10-9 米 B．7×10 -8 米 C．7×10 8 米 D．0.7×10 -8 米6．如图，点O是矩形ABCD的对角线AC的中点，M是CD边的中点．若AB=8，OM=3，则线段OB的长为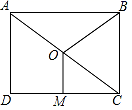（　　）A．5 B．6 C．8 D．107．如图，已知四边形ABCD的对角线AC⊥BD，则顺次连接四边形ABCD各边中点所得的四边形是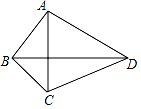（　　）A．矩形 B．菱形 C．正方形 D．平行四边形8．如果等边三角形的边长为4，那么等边三角形的中位线长为A．   B．4    C．6          D．89．直线y=kx+b不经过第三象限，则k、b应满足（  ）A．k＞0，b＜0           B．k＜0，b＞0         C．k＜0  b＜0    D．k＜0，b≥010．化简的结果是A．+1 B． C． D．二、填空题(本大题共有6小题，每小题3分，共18分)11．若关于的一元一次不等式组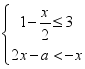所有整数解的和为-9，且关于的分式方程有整数解，则符合条件的所有整数为__________．12．函数的自变量的取值范围是______.13．如图，在平行四边形ABCD中，AB=4，∠ABC=60°，点E为BC上的一点，点F，G分别为DE，AD的中点，则GF长的最小值为________________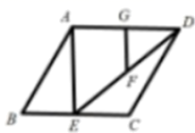．14．在平面直角坐标系中，将点绕点旋转，得到的对应点的坐标是__________．15．如图是由6个形状大小完全相同菱形组成的网格，若菱形的边长为1，一个内角(∠O)为60°，△ABC的各顶点都在格点上，则BC边上的高为______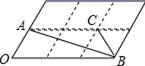．16．如图，在中，，，点D在边上，若以、为边，以为对角线，作，则对角线的最小值为_______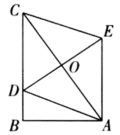．三、解下列各题(本大题共8小题，共72分)17．（8分）阅读下列材料：数学课上，老师出示了这样一个问题：如图1，正方形为中，点、在对角线上，且，探究线段、、之间的数量关系，并证明.某学习小组的同学经过思考，交流了自己的想法：小明：“通过观察和度量，发现与存在某种数量关系”；小强：“通过观察和度量，发现图1中线段与相等”；小伟：“通过构造（如图2），证明三角形全等，进而可以得到线段、、之间的数量关系”.老师：“此题可以修改为‘正方形中，点在对角线上，延长交于点，在上取一点，连接（如图3）.如果给出、的数量关系与、的数量关系，那么可以求出的值”.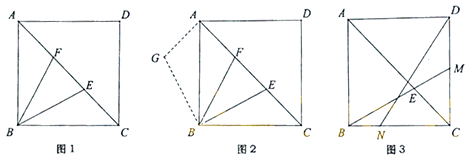请回答：（1）求证：；（2）探究线段、、之间的数量关系，并证明；（3）若，，求的值（用含的代数式表示）.   18．（8分）如图，已知抛物线y＝ax2+bx+1与x轴分别交于A(﹣1，0)，B(3，0)，与y轴交于点C．(1)求抛物线解析式；(2)在直线BC上方的抛物线上有点P，使△PBC面积为1，求出点P的坐标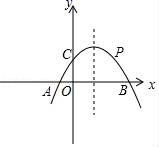．   19．（8分）用圆规、直尺作图，不写作法，但要保留作图痕迹．已知：四边形ABCD求作：点P，使∠PBC＝∠PCB，且点P到AD和DC的距离相等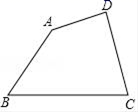．   20．（8分）已知关于的一次函数，求满足下列条件的m的取值范围：（1）函数值y 随x的增大而增大；（2）函数图象与y 轴的负半轴相交；（3）函数的图象过原点.   21．（8分）如图，矩形ABCD中，AB＞AD，把矩形沿对角线AC所在直线折叠，使点B落在点E处，AE交CD于点F，连接DE，求证：∠DAE＝∠ECD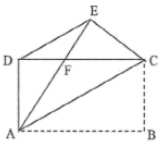．   22．（10分）综合与探究问题情境：在综合实践课上，李老师让同学们根据如下问题情境，写出两个数学结论：如图（1），正方形ABCD的对角线交于点O，点O又是正方形OEFG的一个顶点（正方形OEFG的边长足够长），将正方形OEFG绕点O做旋转实验，OE与BC交于点M，OG与DC交于点N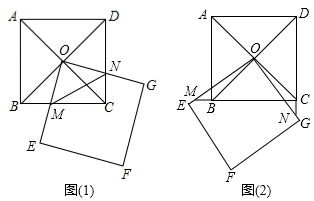．“兴趣小组”写出的两个数学结论是：①S△OMC+S△ONC＝S正方形ABCD；②BM1+CM1＝1OM1．问题解决：（1）请你证明“兴趣小组”所写的两个结论的正确性．类比探究：（1）解决完“兴趣小组”的两个问题后，老师让同学们继续探究，再提出新的问题；“智慧小组“提出的问题是：如图（1），将正方形OEFG在图（1）的基础上旋转一定的角度，当OE与CB的延长线交于点M，OG与DC的延长线交于点N，则“兴趣小组”所写的两个结论是否仍然成立？请说明理由．   23．（10分）（1）因式分解：x3﹣8x2+16x．（2）解方程：2﹣＝．   24．（12分）五一期间，甲、乙两人分别骑自行车和摩托车从地出发前往地郊游，并以各自的速度匀速行驶，到达目的地停止，途中乙休息了一段时间，然后又继续赶路.甲、乙两人各自行驶的路程与所用时间之间的函数图象如图所示.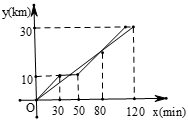(1)甲骑自行车的速度是_____.(2)求乙休息后所行的路程与之间的函数关系式，并写出自变量的取值范围.(3)为了保证及时联络，甲、乙两人在第一次相遇时约定此后两人之间的路程不超过.甲、乙两人是否符合约定，并说明理由.   参考答案 一、选择题(每小题3分,共30分)1、C2、B3、C4、D5、A6、A7、A8、A9、D．10、D 二、填空题(本大题共有6小题，每小题3分，共18分)11、-4，-1．12、x>13、14、15、16、1 三、解下列各题(本大题共8小题，共72分)17、（1）详见解析；（2），证明详见解析；（3）18、 (1)y＝﹣x2+x+1；(2)点P的坐标为(1，)或(2，1)．19、图形见解析.20、（1）,（2）,（3）21、见解析,22、（1）详见解析；（1）结论①不成立，结论②成立，理由详见解析.23、（1）x（x﹣4）1；（1）x＝24、 (1)0.25km/min；(2)(50≤x≤1)；(3)甲、乙两人符合约定．