内蒙古自治区满洲里市2022-2023学年数学七下期末学业水平测试试题含答案

内蒙古自治区满洲里市2022-2023学年数学七下期末学业水平测试试题

（时间：120分钟             分数：120分）

学校_______            年级_______        姓名_______

注意事项

1．考试结束后，请将本试卷和答题卡一并交回．

2．答题前，请务必将自己的姓名、准考证号用0．5毫米黑色墨水的签字笔填写在试卷及答题卡的规定位置．

3．请认真核对监考员在答题卡上所粘贴的条形码上的姓名、准考证号与本人是否相符．

4．作答选择题，必须用2B铅笔将答题卡上对应选项的方框涂满、涂黑；如需改动，请用橡皮擦干净后，再选涂其他答案．作答非选择题，必须用05毫米黑色墨水的签字笔在答题卡上的指定位置作答，在其他位置作答一律无效．

5．如需作图，须用2B铅笔绘、写清楚，线条、符号等须加黑、加粗．

一、选择题(每小题3分,共30分)

1．下列各组长度的线段能组成直角三角形的是（     ）．

A．a=2，b=3，c=4 B．a=4，b=4，c=5

C．a=5，b=6，c=7 D．a=5，b=12，c=13

2．若正比例函数的图象经过点和点，当时，，则的取值范围是（ ）

A． B． C． D．

3．在学校举行的“阳光少年，励志青年”的演讲比赛中，五位评委给选手小明的评分分别为：90，85，90，80，95，则这组数据的众数是(    )

A．95 B．90 C．85 D．80

4．如图，点P为定角∠AOB的平分线上的一个定点，且∠MPN与∠AOB互补，若∠MPN在绕点P旋转的过程中，其两边分别与OA、OB相交于M、N两点，则以下结论：（1）PM=PN恒成立；（2）OM+ON的值不变；（3）四边形PMON的面积不变；（4）MN的长不变，其中正确的个数为（　　）

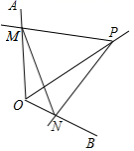
A．4 B．3 C．2 D．1

5．如图，若DE是△ABC的中位线，△ADE的周长为1，则△ABC的周长为（　　）

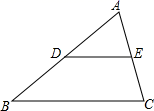
A．1 B．2 C．3 D．4

6．关于函数，下列结论正确的是　　

A．图象必经过点 B．y随x的增大而减小

C．图象经过第一、二、四象限 D．以上都不对

7．P1（x1，y1），P2（x2，y2）是正比例函数y=﹣x图象上的两点，则下列判断正确的是（ ）

A．y1＞y2

B．y1＜y2

C．当x1＜x2时，y1＞y2

D．当x1＜x2时，y1＜y2

8．我国南宋著名数学家秦九韶的著作《数书九章》里记载有这样一道题：“问有沙田一块，有三斜，其中小斜五里，中斜十二里，大斜十三里，欲知为田几何？”这道题讲的是：有一块三角形沙田，三条边长分别为5里，12里，13里，问这块沙田面积有多大？题中“里”是我国市制长度单位，1里=500米，则该沙田的面积为（　　）

A．7.5平方千米 B．15平方千米 C．75平方千米 D．750平方千米

9．若分式有意义，则的取值范围是(  )

A． B． C． D．

10．已知关于x的不等式组无解，则a的取值范围是（    ）

A．a＜3 B．a≤3 C．a＞3 D．a≥3

二、填空题(本大题共有6小题，每小题3分，共18分)

11．设a是的小数部分，则根式可以用表示为______.

12．设甲组数：1，1，2，5的方差为S甲2，乙组数是：6，6，6，6的方差为S乙2，则S甲2与S乙2的大小关系是S甲2_____S乙2（选择“＞”、“＜”或“=”填空）．

13．若是一元二次方程的一个根，则根的判别式与平方式的大小比较_____（填＞，＜或=）.

14．已知有两点、都在一次函数的图象上，则的大小关系是______（用“<”连接）

15．如图，正方形ABCD的边长为8，点E是BC上的一点，连接AE并延长交射线DC于点F，将△ABE沿直线AE翻折，点B落在点N处，AN的延长线交DC于点M，当AB＝2CF时，则NM的长为_____．

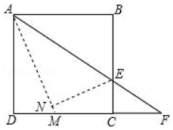
16．若则关于x的方程的解是___________.

三、解下列各题(本大题共8小题，共72分)

17．（8分）如图，等腰△ABC中，已知AC＝BC＝2， AB＝4，作∠ACB的外角平分线CF，点E从点B沿着射线BA以每秒2个单位的速度运动，过点E作BC的平行线交CF于点F．

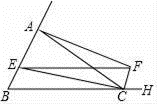
（1）求证：四边形BCFE是平行四边形；   

（2）当点E是边AB的中点时，连接AF，试判断四边形AECF的形状，并说明理由；   

（3）设运动时间为t秒，是否存在t的值，使得以△EFC的其中两边为邻边所构造的平行四边形恰好是菱形？不存在的，试说明理由；存在的，请直接写出t的值．答：t＝________．

18．（8分）（1）在图中以正方形的格点为顶点，画一个三角形，使三角形的边长分别为、2、；

（2）求此三角形的面积及最长边上的高.

19．（8分）解方程

；

.

20．（8分）某学校为了改善办学条件，计划购置一批电子白板和一批笔记本电脑，经投标，购买1块电子白板比买3台笔记本电脑多3000元，购买4块电子白板和5台笔记本电脑共需80000元．

（1）求购买1块电子白板和一台笔记本电脑各需多少元？

（2）根据该校实际情况，需购买电子白板和笔记本电脑的总数为396，要求购买的总费用不超过2700000元，并购买笔记本电脑的台数不超过购买电子白板数量的3倍，该校有哪几种购买方案？

（3）上面的哪种购买方案最省钱？按最省钱方案购买需要多少钱？

21．（8分）如图,已知一次函数y= x−3与反比例函数y= 的图象相交于点A(4,n)，与x轴相交于点B．

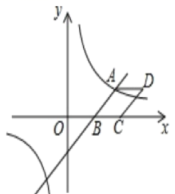
(1)填空：n的值为___，k的值为___；

(2)以AB为边作菱形ABCD，使点C在x轴正半轴上，点D在第一象限，求点D的坐标；

(3)观察反比例函数y=的图象，当y⩾−2时，请直接写出自变量x的取值范围。

22．（10分）小王开车从甲地到乙地，去时走A线路，全程约100千米，返回时走B路线，全程约60千米.小王开车去时的平均速度比返回时的平均速度快20千米/小时，所用时间却比返回时多15分钟.若小王返回时的平均车速不低于70千米/小时，求小王开车返回时的平均速度.

23．（10分）如图所示，已知一次函数的图像直线AB经过点(0,6)和点(-2,0).

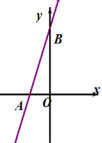
（1）求这个函数的解析式;

（2）直线AB与x轴交于点A，与y轴交于点B，求△AOB的面积.

24．（12分）解方程：

（1）        （2）        （3）

参考答案

一、选择题(每小题3分,共30分)

1、D

2、D

3、B

4、B

5、B

6、A

7、C

8、A

9、A

10、B

二、填空题(本大题共有6小题，每小题3分，共18分)

11、

12、＞

13、=

14、

15、

16、或

三、解下列各题(本大题共8小题，共72分)

17、（1）见解析；（2）四边形AECF是矩形，理由见解析；（3）秒或5秒或2秒

18、（1）三角形画对  （2）三角形面积是5  高是 

19、（1），；（2），．

20、（1）购买1块电子白板需要15000元，一台笔记本电脑需要4000元（2）有三种购买方案：方案一：购买笔记本电脑295台，则购买电子白板101块；方案二：购买笔记本电脑296台，则购买电子白板100块；方案三：购买笔记本电脑297台，则购买电子白板99块.（3）当购买笔记本电脑297台、购买电子白板99块时，最省钱，共需费用2673000元

21、（1）n=3,k=12；（2）(4+,3)；（3）x⩽−6或x>0.

22、80千米/小时

23、 (1)一次函数的解析式为：y=3x+6；(2)△AOB的面积=×6×2=6.

24、（1），.（2），.（3）原方程无解