


北京理工大附属中学2022-2023学年数学七下期末学业水平测试试题含答案
展开
这是一份北京理工大附属中学2022-2023学年数学七下期末学业水平测试试题含答案,共7页。试卷主要包含了考生要认真填写考场号和座位序号,下列条件中能构成直角三角形的是,下列各式中正确的是等内容,欢迎下载使用。
北京理工大附属中学2022-2023学年数学七下期末学业水平测试试题(时间:120分钟 分数:120分) 学校_______ 年级_______ 姓名_______ 注意事项1.考生要认真填写考场号和座位序号。2.试题所有答案必须填涂或书写在答题卡上,在试卷上作答无效。第一部分必须用2B 铅笔作答;第二部分必须用黑色字迹的签字笔作答。3.考试结束后,考生须将试卷和答题卡放在桌面上,待监考员收回。 一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.Rt△ABC中,斜边BC=2,则AB2+AC2+BC2的值为( )A.8 B.4 C.6 D.无法计算2.用反证法证明命题“在![]() 中,若
中,若![]() ,则
,则![]() ”时,可以先假设( )A.
”时,可以先假设( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 3.如图,在△ABC中,BF平分∠ABC,过A点作AF⊥BF,垂足为F并延长交BC于点G,D为AB中点,连接DF延长交AC于点E。若AB=12,BC=20,则线段EF的长为( )
3.如图,在△ABC中,BF平分∠ABC,过A点作AF⊥BF,垂足为F并延长交BC于点G,D为AB中点,连接DF延长交AC于点E。若AB=12,BC=20,则线段EF的长为( )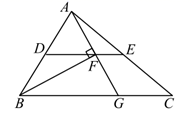 A.2 B.3 C.4 D.54.菱形的两条对角线长为6 cm 和8 cm,那么这个菱形的周长为A.40 cm B.20 cm C.10 cm D.5 cm5.如图,▱ABCD的对角线AC、BD交于点O,AE平分∠BAD交BC于点E,且∠ADC=60°,AB=
A.2 B.3 C.4 D.54.菱形的两条对角线长为6 cm 和8 cm,那么这个菱形的周长为A.40 cm B.20 cm C.10 cm D.5 cm5.如图,▱ABCD的对角线AC、BD交于点O,AE平分∠BAD交BC于点E,且∠ADC=60°,AB=![]() BC,连接OE.下列结论:①∠CAD=30°;②S▱ABCD=AB•AC;③OB=AB;④OE=
BC,连接OE.下列结论:①∠CAD=30°;②S▱ABCD=AB•AC;③OB=AB;④OE=![]() BC,成立的个数有()
BC,成立的个数有() A.1个B.2个C.3个D.4个6.如图,在正方形
A.1个B.2个C.3个D.4个6.如图,在正方形![]() 中,点
中,点![]() 在
在![]() 上,
上,![]() ,垂足分别为
,垂足分别为![]() ,
,![]() ,则
,则![]() 的长为( )
的长为( )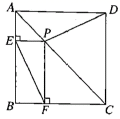 A.1.5 B.2 C.2.5 D.37.下列条件中能构成直角三角形的是( ).A.2、3、4 B.3、4、5 C.4、5、6 D.5、6、78.要使分式
A.1.5 B.2 C.2.5 D.37.下列条件中能构成直角三角形的是( ).A.2、3、4 B.3、4、5 C.4、5、6 D.5、6、78.要使分式![]() 有意义,则x的取值应满足( )A.x≠2 B.x=2 C.x=1 D.x≠19.如图,这是用面积为24的四个全等的直角三角形△ABE,△BCF,△CDG和△DAH拼成的“赵爽弦图”,如果AB=10,那么正方形EFGH的边长为( )
有意义,则x的取值应满足( )A.x≠2 B.x=2 C.x=1 D.x≠19.如图,这是用面积为24的四个全等的直角三角形△ABE,△BCF,△CDG和△DAH拼成的“赵爽弦图”,如果AB=10,那么正方形EFGH的边长为( )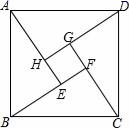 A.1 B.2 C.3 D.410.下列各式中正确的是( )A.
A.1 B.2 C.3 D.410.下列各式中正确的是( )A.![]() B.
B.![]() C.
C.![]() =a+b D.
=a+b D.![]() =-a-b11.如图,在
=-a-b11.如图,在![]() 中,对角线
中,对角线![]() 、
、![]() 相交于点
相交于点![]() ,且
,且![]() ,
,![]() ,则
,则![]() 的度数为( )
的度数为( )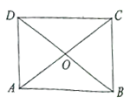 A.35° B.40° C.45° D.55°12.如图,直线
A.35° B.40° C.45° D.55°12.如图,直线![]() 过点
过点![]() 和点
和点![]() ,则方程
,则方程![]() 的解是( )
的解是( )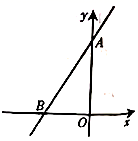 A.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 二、填空题(每题4分,满分20分,将答案填在答题纸上)13.函数
二、填空题(每题4分,满分20分,将答案填在答题纸上)13.函数![]() 中,自变量
中,自变量![]() 的取值范围是__________.14.如图,在反比例函数
的取值范围是__________.14.如图,在反比例函数![]() 的图像上有点
的图像上有点![]() 它们的横坐标依次为1,2,3,……,n,n+1,分别过点
它们的横坐标依次为1,2,3,……,n,n+1,分别过点![]() 作x轴,y轴的垂线,图中所构成的阴影部分面积从左到右依次为
作x轴,y轴的垂线,图中所构成的阴影部分面积从左到右依次为![]() ,则Sn=__________。(用含n的代数式表示)
,则Sn=__________。(用含n的代数式表示)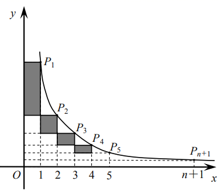 15.如图,平行四边形ABCD的面积为32,对角线BD绕着它的中点O按顺时针方向旋转一定角度后,其所在直线分别交BC,AD于点E、F,若AF=3DF,则图中阴影部分的面积等于_____
15.如图,平行四边形ABCD的面积为32,对角线BD绕着它的中点O按顺时针方向旋转一定角度后,其所在直线分别交BC,AD于点E、F,若AF=3DF,则图中阴影部分的面积等于_____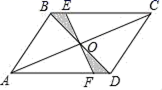 16.如果直线l与直线y=﹣2x+1平行,与直线y=﹣x+2的交点纵坐标为1,那么直线l的函数解析式为__.17.不等式组
16.如果直线l与直线y=﹣2x+1平行,与直线y=﹣x+2的交点纵坐标为1,那么直线l的函数解析式为__.17.不等式组![]() 的解集为_____.三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)18.(5分)已知,如图,在平面直角坐标系
的解集为_____.三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)18.(5分)已知,如图,在平面直角坐标系![]() 中,直线
中,直线![]() 分别交
分别交![]() 轴、
轴、![]() 轴于点
轴于点![]() 、
、![]() 两点,直线
两点,直线![]() 过原点且与直线
过原点且与直线![]() 相交于
相交于![]() ,点
,点![]() 为
为![]() 轴上一动点. (1)求点
轴上一动点. (1)求点![]() 的坐标;(2)求出
的坐标;(2)求出![]() 的面积;(3)当
的面积;(3)当![]() 的值最小时,求此时点
的值最小时,求此时点![]() 的坐标;
的坐标;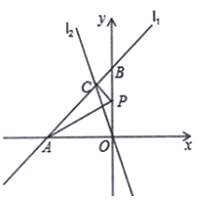 19.(5分)我们知道:等腰三角形两腰上的高相等.
19.(5分)我们知道:等腰三角形两腰上的高相等. (1)请你写出它的逆命题:______.(2)逆命题是真命题吗?若是,请证明;若不是,请举出反例(要求:画出图形,写出已知,求证和证明过程). 20.(8分)勾股定理神秘而美妙,它的证法多样,其巧妙各有不同,其中的“面积法”给了小聪以灵感,他惊喜的发现,当两个全等的直角三角形如图1或图1摆放时,都可以用“面积法”来证明,请你利用图1或图1证明勾股定理(其中∠DAB=90°)求证:a1+b1=c1.
(1)请你写出它的逆命题:______.(2)逆命题是真命题吗?若是,请证明;若不是,请举出反例(要求:画出图形,写出已知,求证和证明过程). 20.(8分)勾股定理神秘而美妙,它的证法多样,其巧妙各有不同,其中的“面积法”给了小聪以灵感,他惊喜的发现,当两个全等的直角三角形如图1或图1摆放时,都可以用“面积法”来证明,请你利用图1或图1证明勾股定理(其中∠DAB=90°)求证:a1+b1=c1.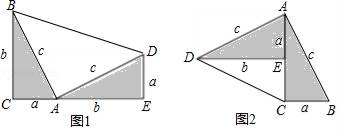 21.(10分)有一次,小明坐着轮船由A点出发沿正东方向AN航行,在A点望湖中小岛M,测得∠MAN=30°,航行100米到达B点时,测得∠MBN=45°,你能算出A点与湖中小岛M的距离吗?
21.(10分)有一次,小明坐着轮船由A点出发沿正东方向AN航行,在A点望湖中小岛M,测得∠MAN=30°,航行100米到达B点时,测得∠MBN=45°,你能算出A点与湖中小岛M的距离吗?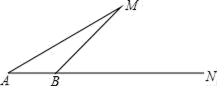 22.(10分)解不等式组:
22.(10分)解不等式组: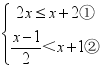 请结合题意填空,完成本题解答:(1)解不等式①,得______;(2)解不等式②,得______;(3)把不等式①和②的解集在数轴上表示出来;
请结合题意填空,完成本题解答:(1)解不等式①,得______;(2)解不等式②,得______;(3)把不等式①和②的解集在数轴上表示出来;![]() (4)原不等式组的解集为______. 23.(12分)如图,点O为等边三角形ABC内一点,连接OA,OB,OC,将线段BO绕点B顺时针旋转60°到BM,连接CM,OM.
(4)原不等式组的解集为______. 23.(12分)如图,点O为等边三角形ABC内一点,连接OA,OB,OC,将线段BO绕点B顺时针旋转60°到BM,连接CM,OM.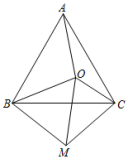 (1)求证:AO=CM; (2)若OA=8,OC=6,OB=10,判断△OMC的形状并证明. 参考答案 一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.1、A2、B3、C4、B5、C6、D7、B8、A9、B10、D11、A12、B 二、填空题(每题4分,满分20分,将答案填在答题纸上)13、x≥0且x≠114、
(1)求证:AO=CM; (2)若OA=8,OC=6,OB=10,判断△OMC的形状并证明. 参考答案 一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.1、A2、B3、C4、B5、C6、D7、B8、A9、B10、D11、A12、B 二、填空题(每题4分,满分20分,将答案填在答题纸上)13、x≥0且x≠114、![]() 15、116、答案为:y=﹣2x+3.17、1<x≤2 三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)18、 (1)点
15、116、答案为:y=﹣2x+3.17、1<x≤2 三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)18、 (1)点![]() ;(2)
;(2)![]() ;(3)点
;(3)点![]() .19、(1)两边上的高相等的三角形是等腰三角形;(2)是,证明见解析.20、见解析.21、A点与湖中小岛M的距离为100+100
.19、(1)两边上的高相等的三角形是等腰三角形;(2)是,证明见解析.20、见解析.21、A点与湖中小岛M的距离为100+100![]() 米;22、(1)x≤2;(2)x>-3;(3)把不等式①和②的解集在数轴上表示见解析;(4)-3<x≤2,23、(1)见解析 (2)直角三角形,证明见解析
米;22、(1)x≤2;(2)x>-3;(3)把不等式①和②的解集在数轴上表示见解析;(4)-3<x≤2,23、(1)见解析 (2)直角三角形,证明见解析








