


呼伦贝尔市2022-2023学年数学七下期末学业水平测试试题含答案
展开
这是一份呼伦贝尔市2022-2023学年数学七下期末学业水平测试试题含答案,共8页。试卷主要包含了如图,已知直线与相交于点等内容,欢迎下载使用。
呼伦贝尔市2022-2023学年数学七下期末学业水平测试试题(时间:120分钟 分数:120分) 学校_______ 年级_______ 姓名_______ 考生须知:1.全卷分选择题和非选择题两部分,全部在答题纸上作答。选择题必须用2B铅笔填涂;非选择题的答案必须用黑色字迹的钢笔或答字笔写在“答题纸”相应位置上。2.请用黑色字迹的钢笔或答字笔在“答题纸”上先填写姓名和准考证号。3.保持卡面清洁,不要折叠,不要弄破、弄皱,在草稿纸、试题卷上答题无效。 一、选择题(每小题3分,共30分)1.关于x的一元二次方程![]() 有两个实数根,则实数m的取值范围是( )A.m≥0 B.m>0 C.m≥0且m≠1 D.m>0且m≠12.平行四边形一边长12,那么它的两条对角线的长度可能是( )A.8和16 B.10和16 C.8和14 D.8和123.如果a<b,则下列式子错误的是( )A.a+2<b+2 B.a-3<b-3 C.-5a<-5b D.
有两个实数根,则实数m的取值范围是( )A.m≥0 B.m>0 C.m≥0且m≠1 D.m>0且m≠12.平行四边形一边长12,那么它的两条对角线的长度可能是( )A.8和16 B.10和16 C.8和14 D.8和123.如果a<b,则下列式子错误的是( )A.a+2<b+2 B.a-3<b-3 C.-5a<-5b D.![]() <
<![]() 4.匀速地向如图的容器内注水,最后把容器注满,在注水过程中,水面的高度h随时间t的变化而变化,变化规律为一折线,下列图象(草图)正确的是( )
4.匀速地向如图的容器内注水,最后把容器注满,在注水过程中,水面的高度h随时间t的变化而变化,变化规律为一折线,下列图象(草图)正确的是( )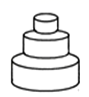 A.
A.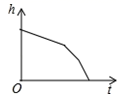 B.
B.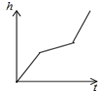 C.
C.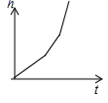 D.
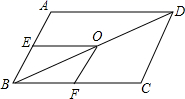
D.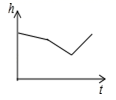 5.如图,在平行四边形ABCD中,BD为对角线,点E、O、F分别是 AB、BD、BC的中点,且
5.如图,在平行四边形ABCD中,BD为对角线,点E、O、F分别是 AB、BD、BC的中点,且![]() ,
,![]() ,则平行四边形ABCD的周长为
,则平行四边形ABCD的周长为![]()
![]()
 A.10 B.12 C.15 D.206.如图,已知直线
A.10 B.12 C.15 D.206.如图,已知直线![]() 与
与![]() 相交于点
相交于点![]() (2,
(2,![]() ),若
),若![]() ,则
,则![]() 的取值范围是( )
的取值范围是( )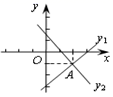 A.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 7.如图所示,在平行四边形
7.如图所示,在平行四边形![]() 中,
中,![]() ,
,![]() ,
,![]() 平分
平分![]() 交
交![]() 边于点
边于点![]() ,则线段
,则线段![]() ,
,![]() 的长度分别为( )
的长度分别为( )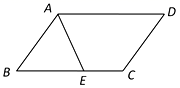 A.4和5 B.5和4 C.6和3 D.3和68.如图,在矩形ABCD中,对角线
A.4和5 B.5和4 C.6和3 D.3和68.如图,在矩形ABCD中,对角线![]() 相交于点
相交于点![]() ,则AB的长是
,则AB的长是![]()
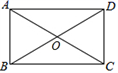 A.3cm B.6cm C.10cm D.12cm9.▱ABCD中,∠A=50°,两条对角线相交于点O,下列结论正确的是( )A.∠ABC=50° B.∠BCD=50° C.AB=BC D.OB=OC10.如图,已知平行四边形
A.3cm B.6cm C.10cm D.12cm9.▱ABCD中,∠A=50°,两条对角线相交于点O,下列结论正确的是( )A.∠ABC=50° B.∠BCD=50° C.AB=BC D.OB=OC10.如图,已知平行四边形![]() ,
,![]() ,
,![]() 分别是
分别是![]() ,
,![]() 边上的点,
边上的点,![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点,若点
的中点,若点![]() 在
在![]() 边上从
边上从![]() 向
向![]() 移动,点
移动,点![]() 不动,那么下列结论成立的是( )
不动,那么下列结论成立的是( )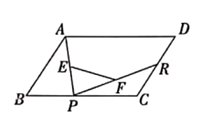 A.
A.![]() B.线段
B.线段![]() 的长度逐渐变小C.线段
的长度逐渐变小C.线段![]() 的长度保持不变 D.线段
的长度保持不变 D.线段![]() 的长度逐渐变大二、填空题(本大题共有6小题,每小题3分,共18分)11.方程
的长度逐渐变大二、填空题(本大题共有6小题,每小题3分,共18分)11.方程![]() 的解是__________.12.如图,小军在地面上合适的位置平放了一块平面镜(平面镜的高度忽略不计),刚好在平面镜中的点
的解是__________.12.如图,小军在地面上合适的位置平放了一块平面镜(平面镜的高度忽略不计),刚好在平面镜中的点![]() 处看到旗杆顶部
处看到旗杆顶部![]() ,此时小军的站立点
,此时小军的站立点![]() 与点
与点![]() 的水平距离为
的水平距离为![]() ,旗杆底部
,旗杆底部![]() 与点
与点![]() 的水平距离为
的水平距离为![]() .若小军的眼睛距离地面的高度为
.若小军的眼睛距离地面的高度为![]() (即
(即![]() ),则旗杆的高度为_____
),则旗杆的高度为_____![]() .
.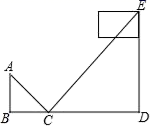 13.如图,AD∥EF∥GH∥PQ∥BC,AE=EG=GP=PB,AD=2,BC=10,则EF+PQ长为__________.
13.如图,AD∥EF∥GH∥PQ∥BC,AE=EG=GP=PB,AD=2,BC=10,则EF+PQ长为__________.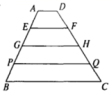 14.如图,在平面直角坐标系中,点M是直线y=﹣x上的动点,过点M作MN⊥x轴,交直线y=x于点N,当MN≤8时,设点M的横坐标为m,则m的取值范围为_______.
14.如图,在平面直角坐标系中,点M是直线y=﹣x上的动点,过点M作MN⊥x轴,交直线y=x于点N,当MN≤8时,设点M的横坐标为m,则m的取值范围为_______.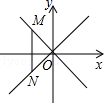 15.已知关于x的方程
15.已知关于x的方程![]() =1的解是负值,则a的取值范围是______.16.如图,矩形ABCD中,
=1的解是负值,则a的取值范围是______.16.如图,矩形ABCD中,![]() ,
,![]() ,CE是
,CE是![]() 的平分线与边AB的交点,则BE的长为______.
的平分线与边AB的交点,则BE的长为______.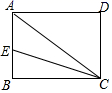 三、解下列各题(本大题共8小题,共72分)17.(8分)已知函数y=x+
三、解下列各题(本大题共8小题,共72分)17.(8分)已知函数y=x+![]() (x>0),它的图象犹如老师的打钩,因此人称对钩函数.下表是y与x的几组对应值:x
(x>0),它的图象犹如老师的打钩,因此人称对钩函数.下表是y与x的几组对应值:x![]()
![]()
![]() 1234y4
1234y4![]() 3
3![]() 2
2![]() 22
22![]() 3
3![]() 4
4![]() 请你根据学习函数的经验,利用上述表格所反映出的y与x之间的变化规律,对该函数的图象与性质进行探究.(1)如图,在平面直角坐标系xOy中,描出了上表中各对对应值为坐标的点,根据描出的点,画出该函数的图象;
请你根据学习函数的经验,利用上述表格所反映出的y与x之间的变化规律,对该函数的图象与性质进行探究.(1)如图,在平面直角坐标系xOy中,描出了上表中各对对应值为坐标的点,根据描出的点,画出该函数的图象;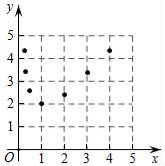 (2)根据画出的函数图象特征,仿照示例,完成下列表格中的函数变化规律:序号函数图象特征函数变化规律示例1在直线x=1右侧,函数图象呈上升状态当x>1时,y随x的增大而增大示例2函数图象经过点(2,2
(2)根据画出的函数图象特征,仿照示例,完成下列表格中的函数变化规律:序号函数图象特征函数变化规律示例1在直线x=1右侧,函数图象呈上升状态当x>1时,y随x的增大而增大示例2函数图象经过点(2,2![]() )当x=2时,y=2
)当x=2时,y=2![]() ①函数图象的最低点是(1,2) ②在直线x=1左侧,函数图象呈下降状态 (3)当a≤x≤4时,y的取值范围为2≤y≤4
①函数图象的最低点是(1,2) ②在直线x=1左侧,函数图象呈下降状态 (3)当a≤x≤4时,y的取值范围为2≤y≤4![]() ,则a的取值范围为 . 18.(8分)(2013年四川广安8分)某商场筹集资金12.8万元,一次性购进空调、彩电共30台.根据市场需要,这些空调、彩电可以全部销售,全部销售后利润不少于1.5万元,其中空调、彩电的进价和售价见表格. 空调彩电进价(元/台)54003500售价(元/台)61003900设商场计划购进空调x台,空调和彩电全部销售后商场获得的利润为y元.(1)试写出y与x的函数关系式;(2)商场有哪几种进货方案可供选择?(3)选择哪种进货方案,商场获利最大?最大利润是多少元? 19.(8分)一次安全知识测验中,学生得分均为整数,满分10分,这次测验中,甲,乙两组学生人数都为5人,成绩如下(单位:分):甲:8,8,7,8,9乙:5,9,7,10,9(1)填写下表: 平均数众数中位数甲______________88乙______________9______________(2)已知甲组学生成绩的方差
,则a的取值范围为 . 18.(8分)(2013年四川广安8分)某商场筹集资金12.8万元,一次性购进空调、彩电共30台.根据市场需要,这些空调、彩电可以全部销售,全部销售后利润不少于1.5万元,其中空调、彩电的进价和售价见表格. 空调彩电进价(元/台)54003500售价(元/台)61003900设商场计划购进空调x台,空调和彩电全部销售后商场获得的利润为y元.(1)试写出y与x的函数关系式;(2)商场有哪几种进货方案可供选择?(3)选择哪种进货方案,商场获利最大?最大利润是多少元? 19.(8分)一次安全知识测验中,学生得分均为整数,满分10分,这次测验中,甲,乙两组学生人数都为5人,成绩如下(单位:分):甲:8,8,7,8,9乙:5,9,7,10,9(1)填写下表: 平均数众数中位数甲______________88乙______________9______________(2)已知甲组学生成绩的方差![]() ,计算乙组学生成绩的方差,并说明哪组学生的成绩更稳定. 20.(8分)完成下面推理过程如图,已知DE∥BC,DF、BE分别平分∠ADE、∠ABC,可推得∠FDE=∠DEB的理由:
,计算乙组学生成绩的方差,并说明哪组学生的成绩更稳定. 20.(8分)完成下面推理过程如图,已知DE∥BC,DF、BE分别平分∠ADE、∠ABC,可推得∠FDE=∠DEB的理由: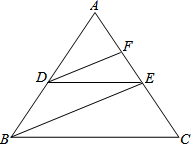 ∵DE∥BC(已知)∴∠ADE= .( ) ∵DF、BE分别平分∠ADE、∠ABC,∴∠ADF=
∵DE∥BC(已知)∴∠ADE= .( ) ∵DF、BE分别平分∠ADE、∠ABC,∴∠ADF=![]() ,∠ABE=
,∠ABE=![]() .( )∴∠ADF=∠ABE∴DF∥ .( )∴∠FDE=∠DEB. ( ) 21.(8分)图(a)、图(b)、图(c)是三张形状、大小完全相同的方格纸,方格纸中的每个小正方形的边长均为1.请在图(a)、图(b)、图(c)中,分别画出符合要求(1),(2),(3)的图形,所画图形各顶点必须与方格纸中的小正方形顶点重合.
.( )∴∠ADF=∠ABE∴DF∥ .( )∴∠FDE=∠DEB. ( ) 21.(8分)图(a)、图(b)、图(c)是三张形状、大小完全相同的方格纸,方格纸中的每个小正方形的边长均为1.请在图(a)、图(b)、图(c)中,分别画出符合要求(1),(2),(3)的图形,所画图形各顶点必须与方格纸中的小正方形顶点重合.

 (1)画一个底边为4,面积为8的等腰三角形;(2)画一个面积为10的等腰直角三角形;(3)画一个面积为12的平行四边形。 22.(10分)在平面直角坐标系xOy中,点P在函数
(1)画一个底边为4,面积为8的等腰三角形;(2)画一个面积为10的等腰直角三角形;(3)画一个面积为12的平行四边形。 22.(10分)在平面直角坐标系xOy中,点P在函数![]() 的图象上,过P作直线
的图象上,过P作直线![]() 轴于点A,交直线
轴于点A,交直线![]() 于点M,过M作直线
于点M,过M作直线![]() 轴于点B.交函数
轴于点B.交函数![]() 的图象于点Q。(1)若点P的横坐标为1,写出点P的纵坐标,以及点M的坐标;(2)若点P的横坐标为t,①求点Q的坐标(用含t的式子表示)②直接写出线段PQ的长(用含t的式子表示) 23.(10分)如图,直线
的图象于点Q。(1)若点P的横坐标为1,写出点P的纵坐标,以及点M的坐标;(2)若点P的横坐标为t,①求点Q的坐标(用含t的式子表示)②直接写出线段PQ的长(用含t的式子表示) 23.(10分)如图,直线![]() 与直线
与直线![]() 相交于点
相交于点![]() .(1)求
.(1)求![]() ,
,![]() 的值;(2)根据图像直接写出
的值;(2)根据图像直接写出![]() 时
时![]() 的取值范围;(3)垂直于
的取值范围;(3)垂直于![]() 轴的直线
轴的直线![]() 与直线
与直线![]() ,
,![]() 分别交于点
分别交于点![]() ,
,![]() ,若线段
,若线段![]() 长为2,求
长为2,求![]() 的值.
的值.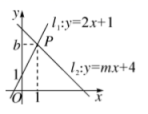 24.(12分)已知一条直线AB经过点(1,4)和(-1,-2)(1)求直线AB的解析式. (2)求直线AB和直线CD:y=x+3的交点M的坐标. 参考答案 一、选择题(每小题3分,共30分)1、C2、B3、C4、C5、D6、B7、B8、A9、B10、C 二、填空题(本大题共有6小题,每小题3分,共18分)11、
24.(12分)已知一条直线AB经过点(1,4)和(-1,-2)(1)求直线AB的解析式. (2)求直线AB和直线CD:y=x+3的交点M的坐标. 参考答案 一、选择题(每小题3分,共30分)1、C2、B3、C4、C5、D6、B7、B8、A9、B10、C 二、填空题(本大题共有6小题,每小题3分,共18分)11、![]() 12、113、114、﹣1≤m≤115、a<-2且a≠-416、
12、113、114、﹣1≤m≤115、a<-2且a≠-416、![]() 三、解下列各题(本大题共8小题,共72分)17、(1)画图见解析;(2):x=1时,y有最小值2,当x<1时,y随x的增大而减小;(3)1≤a≤418、解:(1)设商场计划购进空调x台,则计划购进彩电(30﹣x)台,由题意,得y=(6100﹣5400)x+(3900﹣3500)(30﹣x)=300x+12000。(2)依题意,得
三、解下列各题(本大题共8小题,共72分)17、(1)画图见解析;(2):x=1时,y有最小值2,当x<1时,y随x的增大而减小;(3)1≤a≤418、解:(1)设商场计划购进空调x台,则计划购进彩电(30﹣x)台,由题意,得y=(6100﹣5400)x+(3900﹣3500)(30﹣x)=300x+12000。(2)依题意,得![]() , 解得10≤x≤
, 解得10≤x≤![]() 。∵x为整数,∴x=10,11,12。∴商场有三种方案可供选择:方案1:购空调10台,购彩电20台;方案2:购空调11台,购彩电19台;方案3:购空调12台,购彩电18台。(3)∵y=300x+12000,k=300>0,∴y随x的增大而增大。∴当x=12时,y有最大值,y最大=300×12+12000=15600元.故选择方案3:购空调12台,购彩电18台时,商场获利最大,最大利润是15600元。19、(1)甲:平均数8;乙:平均数8,中位数9;(2)甲组学生的成绩比较稳定.20、∠ABC;两直线平行,同位角相等;
。∵x为整数,∴x=10,11,12。∴商场有三种方案可供选择:方案1:购空调10台,购彩电20台;方案2:购空调11台,购彩电19台;方案3:购空调12台,购彩电18台。(3)∵y=300x+12000,k=300>0,∴y随x的增大而增大。∴当x=12时,y有最大值,y最大=300×12+12000=15600元.故选择方案3:购空调12台,购彩电18台时,商场获利最大,最大利润是15600元。19、(1)甲:平均数8;乙:平均数8,中位数9;(2)甲组学生的成绩比较稳定.20、∠ABC;两直线平行,同位角相等;![]() ∠ADE;
∠ADE;![]() ∠ABC;角平分线定义;DF∥BE;同位角相等,两直线平行;两直线平行,内错角相等21、如图所示:
∠ABC;角平分线定义;DF∥BE;同位角相等,两直线平行;两直线平行,内错角相等21、如图所示: 22、(1)点P的纵坐标为4,点M的坐标为
22、(1)点P的纵坐标为4,点M的坐标为![]() ;(2)①
;(2)①![]() ;②
;②![]() 23、(1)
23、(1)![]() ,
,![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 或
或![]() 24、(1)y=3x+1;(2)M(1,4).
24、(1)y=3x+1;(2)M(1,4).
相关试卷
这是一份2022-2023学年陈经纶中学七下数学期末学业水平测试模拟试题含答案,共7页。试卷主要包含了考生必须保证答题卡的整洁等内容,欢迎下载使用。
这是一份2022-2023学年辽宁省数学七下期末学业水平测试模拟试题含答案,共7页。试卷主要包含了答题时请按要求用笔,下列二次根式能与合并的是等内容,欢迎下载使用。
这是一份2022-2023学年甘肃省七下数学期末学业水平测试模拟试题含答案,共6页。试卷主要包含了答题时请按要求用笔等内容,欢迎下载使用。








