天津市红桥区复兴中学2022-2023学年七下数学期末学业水平测试试题含答案

这是一份天津市红桥区复兴中学2022-2023学年七下数学期末学业水平测试试题含答案，共7页。试卷主要包含了下列判断中，错误的是，如图，直线y=kx+3经过点等内容，欢迎下载使用。
天津市红桥区复兴中学2022-2023学年七下数学期末学业水平测试试题（时间：120分钟             分数：120分） 学校_______            年级_______        姓名_______ 注意事项1．考试结束后，请将本试卷和答题卡一并交回．2．答题前，请务必将自己的姓名、准考证号用0．5毫米黑色墨水的签字笔填写在试卷及答题卡的规定位置．3．请认真核对监考员在答题卡上所粘贴的条形码上的姓名、准考证号与本人是否相符．4．作答选择题，必须用2B铅笔将答题卡上对应选项的方框涂满、涂黑；如需改动，请用橡皮擦干净后，再选涂其他答案．作答非选择题，必须用05毫米黑色墨水的签字笔在答题卡上的指定位置作答，在其他位置作答一律无效．5．如需作图，须用2B铅笔绘、写清楚，线条、符号等须加黑、加粗． 一、选择题(每小题3分,共30分)1．某社区超市以4元/瓶从厂家购进一批饮料，以6元/瓶销售.近期计划进行打折销售，若这批饮料的销售利润不低于20%则最多可以打（      ）A．六折 B．七折 C．七五折 D．八折2．如图，函数y=2x-4与x轴．y轴交于点（2，0），（0，-4），当-4＜y＜0时，x的取值范围是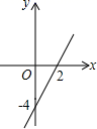（       ）A．x＜-1 B．-1＜x＜0 C．0＜x＜2 D．-1＜x＜23．如图，在平面直角坐标系中，直线与双曲线交于、两点，且点的坐标为，将直线向上平移个单位，交双曲线于点，交轴于点，且的面积是．给出以下结论：（1）；（2）点的坐标是；（3）；（4）．其中正确的结论有　　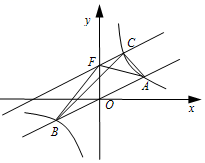A．1个 B．2个 C．3个 D．4个4．如图，在中，，AD平分，，，那么点D到直线AB的距离是（    ）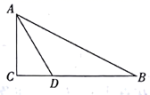A．2cm B．4cm C．6cm D．10cm5．下列式子中，属于最简二次根式的是（　　 ）A． B． C． D．6．一个多边形的内角和是外角和的2倍，这个多边形是(　　)A．四边形 B．五边形 C．六边形 D．八边形7．如图，在四边形ABCD中，∠A+∠D=α，∠ABC的平分线与∠BCD的平分线交于点P，则∠P=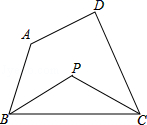（　　） A．90°-α B．90°+ α C． D．360°-α8．下列判断中，错误的是（　　）A．方程是一元二次方程 B．方程是二元二次方程C．方程是分式方程 D．方程是无理方程9．如图，直线y=kx+3经过点（2，0），则关于x的不等式kx+3＞0的解集是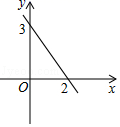（　　）A．x＞2 B．x＜2 C．x≥2 D．x≤210．点、均在由边长为1的正方形组成的网格的格点上，建立平面直角坐标系如图所示。若是轴上使得的值最大的点，是轴上使得的值最小的点，则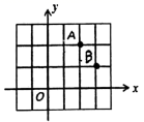（    ）A．4 B．6.3 C．6.4 D．5二、填空题(本大题共有6小题，每小题3分，共18分)11．已知中，，点为边的中点，若，则长为__________．12．四边形ABCD为菱形，该菱形的周长为16，面积为8，则∠ABC为_____度．13．某中学组织初二学生开展篮球比赛，以班为单位单循环形式（每两班之间赛一场），现计划安排15场比赛，则共有多少个班级参赛？设有x个班级参赛，根据题意，可列方程为_____．14．函数y＝中，自变量x的取值范围是_____．15．已知关于X的一元二次方程有实数根，则m的取值范围是____________________16．若正数a是一元二次方程x2﹣5x+m=0的一个根，﹣a是一元二次方程x2+5x﹣m=0的一个根，则a的值是______．三、解下列各题(本大题共8小题，共72分)17．（8分）解不等式组，并在数轴上把解集表示出来．(1)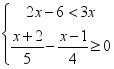(2)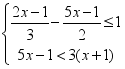   18．（8分）如图，在△ABC中，点O是AC边上一动点，过点O作BC的平行线交∠ACB的角平分线于点E，交∠ACB的外角平分线于点F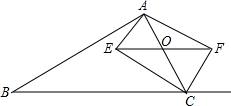（1）求证：EO＝FO；（2）当点O运动到何处时，四边形CEAF是矩形？请证明你的结论．（3）在第（2）问的结论下，若AE＝3，EC＝4，AB＝12，BC＝13，请直接写出凹四边形ABCE的面积为　   　．   19．（8分）如图，在正方形ABCD中，E、F分别为AB、BC的中点，连接CE、DF，将△CBE沿CE对折，得到△CGE，延长EG交CD的延长线于点H。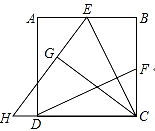（1）求证：CE⊥DF；（2）求的值．   20．（8分）如图，在中，，CD平分，，，E，F是垂足，那么四边形CEDF是正方形吗？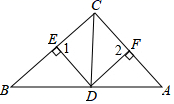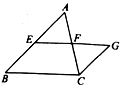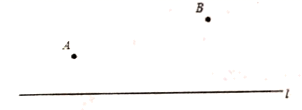说出理由．   21．（8分）如图，在中，点，分别为边，的中点，延长到点使．求证：四边形是平行四边形．   22．（10分）如图，抛物线与轴交于，两点在的左侧），与轴交于点．（1）求点，点的坐标；（2）求的面积；（3）为第二象限抛物线上的一个动点，求面积的最大值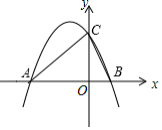．   23．（10分）用圆规、直尺作图，不写作法，但要保留作图痕迹．如图，已知点，点和直线． （1）在直线上求作一点，使最短；（2）请在直线上任取一点（点与点不重合），连接和，试说明．   24．（12分）某零件制造车间有工人20名，已知每名工人每天可制造甲种零件6个或乙种零件5个，且每制造一个甲种零件，可获利润150元，每制造一个乙种零件可获利润260元，在这20名工人中，车间每天安排名工人制造甲种零件，其余工人制造乙种零件，且生产乙种零件的个数不超过甲种零件个数的一半．（1）请写出此车间每天所获利润（元）与（人）之间的函数关系式；（2）求自变量的取值范围；（3）怎样安排生产每天获得的利润最大，最大利润是多少？   参考答案 一、选择题(每小题3分,共30分)1、D2、C3、C4、B5、B6、C7、C8、D9、B10、C 二、填空题(本大题共有6小题，每小题3分，共18分)11、12、30或15013、14、x≥1．15、m≤3且m≠216、1 三、解下列各题(本大题共8小题，共72分)17、（1），数轴见解析；（2），数轴见解析18、（1）详见解析；（2）当点O运动到AC的中点时，四边形CEAF是矩形，理由详见解析；（3）1．19、（1）见解析；（2）.20、是，理由见解析.21、证明见解析．22、（1），；（2）；（3）当时，最大面积4.23、（1）作图见解析；（2）证明见解析24、（1）；（2）（3）安排13人生产甲种零件，安排7人生产乙种零件，所获利润最大，最大利润为20800元．