






【同步学案】苏教版(2019) 高中数学 第13章立体几何初步13.3空间图形的表面积和体积学案含解析
展开13.3 空间图形的表面积和体积
13.3.1 空间图形的表面积
学 习 任 务 | 核 心 素 养 |
1.了解直棱柱、正棱柱、正棱锥、正棱台的几何特征.(重点) 2.了解柱、锥、台的表面积的计算公式.(易错点) 3.会求直棱柱、正棱锥、正棱台、圆柱、圆锥和圆台的表面积.(重点、难点) | 1.通过对柱、锥、台的侧面展开,培养直观想象素养. 2.通过利用柱、锥、台的侧面积和表面积计算公式,培养数学运算素养. |
![]()
![]()
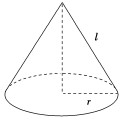
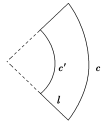
1.在下图中,哪些图形是空间图形的展开图?
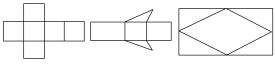
2.下图中分别是哪些空间图形的侧面展开图?
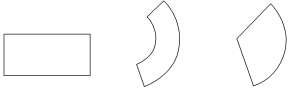
知识点1 几种特殊的多面体
(1)直棱柱:侧棱和底面垂直的棱柱叫作直棱柱.
(2)正棱柱:底面为正多边形的直棱柱叫作正棱柱.
(3)正棱锥:一个棱锥的底面是正多边形,并且顶点在底面的射影是底面中心,那么称这样的棱锥为正棱锥.正棱锥的侧棱长都相等,侧面均为全等的等腰三角形.
(4)正棱台:正棱锥被平行于底面的平面所截,截面和底面之间的部分叫作正棱台.
![]() 1.思考辨析(正确的画“√”,错误的画“×”)
1.思考辨析(正确的画“√”,错误的画“×”)
(1)棱长都相等的长方体是正方体. ( )
(2)有两个相邻侧面为矩形的棱柱为直棱柱. ( )
(3)有两个侧面与底面垂直的棱柱为直棱柱. ( )
(4)底面为菱形,且有一个顶点处的三条棱两两垂直的棱柱是正四棱柱. ( )
[答案] (1)√ (2)√ (3)× (4)√
知识点2 几种简单空间图形的侧面展开图与侧面积
空间图形 | 直观图 | 侧面展开图 | 侧面积 |
直(正)棱柱 |
|
| S直(正)棱柱侧=ch |
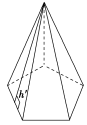
正棱锥 |
|
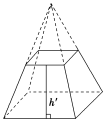
| S正棱锥侧=ch′ |
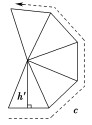
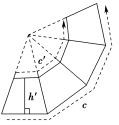
正棱台 |
|
| S正棱台侧=(c+c′)h′ |
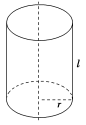
圆柱 |
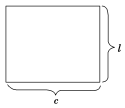
|
| S圆柱侧=cl=2πrl |
圆锥 |
|
| S圆锥侧=cl=πrl |
圆台 |
|
| S圆台侧=(c+c′)l=π(r+r′)l |
![]() 圆柱、圆锥、圆台的侧面积公式之间的关系?
圆柱、圆锥、圆台的侧面积公式之间的关系?
[提示] S圆柱侧=2πrlS圆台侧=π(r′+r)lS圆锥侧=πrl.
![]() 2.正三棱锥的底面边长为a,高为a,则此棱锥的侧面积为________.
2.正三棱锥的底面边长为a,高为a,则此棱锥的侧面积为________.
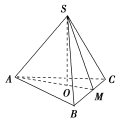 a2 [如图,在正三棱锥SABC中,过点S作SO⊥平面ABC于O点,则O为△ABC的中心,连接AO并延长与BC相交于点M,连接SM,SM即为斜高h′,在Rt△SMO中,h′= =a,所以侧面积S=3××a×a=a2.]
a2 [如图,在正三棱锥SABC中,过点S作SO⊥平面ABC于O点,则O为△ABC的中心,连接AO并延长与BC相交于点M,连接SM,SM即为斜高h′,在Rt△SMO中,h′= =a,所以侧面积S=3××a×a=a2.]
![]() 3.以边长为1的正方形的一边所在直线为旋转轴,将该正方形旋转一周所得圆柱的侧面积等于________.
3.以边长为1的正方形的一边所在直线为旋转轴,将该正方形旋转一周所得圆柱的侧面积等于________.
2π [以正方形的一边所在直线为轴旋转得到的圆柱底面半径r=1,高h=1,所以侧面积S=2πrh=2π.]
![]()
![]() 类型1 棱柱、棱锥和棱台的侧面积和表面积
类型1 棱柱、棱锥和棱台的侧面积和表面积
【例1】 正四棱锥的侧面积是底面积的2倍,高是3 cm,求它的表面积.
![]()
由S侧与S底的关系,求得斜高与底面边长之间的关系,进而求出斜高和底面边长,最后求表面积.
![]()
[解] 如图,设PO=3(cm),PE是斜高,
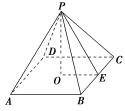
∵S侧=2S底,
∴4××BC×PE=2BC2.
∴BC=PE.
在Rt△POE中,PO=3(cm),OE=BC=PE.
∴9+=PE2,
∴PE=2(cm).
∴S底=BC2=PE2=(2)2=12(cm2).
S侧=2S底=2×12=24(cm2).
∴S表=S底+S侧=12+24=36(cm2).
![]()
求棱锥、棱台及棱柱的侧面积和表面积的关键是求底面边长,高,斜高,侧棱.求解时要注意直角三角形和梯形的应用.
![]()
[跟进训练]
1.已知一个三棱台的上、下底面分别是边长为20 cm和30 cm的正三角形,侧面是全等的等腰梯形,且侧面面积等于上、下底面面积之和,求棱台的高.
[解] 如图所示,在三棱台ABCA′B′C′中,O′,O分别为上、下底面的中心,D,D′分别是BC,B′C′的中点,则DD′是等腰梯形BCC′B′的高,
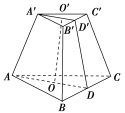
所以S侧=3××(20+30)×DD′=75DD′(cm2).
又A′B′=20 cm,AB=30 cm,则上、下底面面积之和为S上+S下=×(202+302)=325(cm2).
由S侧=S上+S下,得75DD′=325,
所以DD′= (cm),
又因为O′D′=×20=(cm),
OD=×30=5(cm),
所以棱台的高h=O′O=
=
=4(cm).
![]() 类型2 圆柱、圆锥和圆台的侧面积和表面积
类型2 圆柱、圆锥和圆台的侧面积和表面积
【例2】 已知圆锥的底面半径为R,高为3R.若它的内接圆柱的底面半径为R,求该圆柱的全面积.
[解] 设圆柱底面半径为r,高为h,
由题意知r=R,∴=,∴h=R,
∴S圆柱全=2πr2+2πrh=2π+2π=πR2.
![]()
1.圆柱、圆锥、圆台的相关几何量都集中体现在轴截面上,因此准确把握轴截面中相关量是求解旋转体表面积的关键.
2.解决柱体、锥体、台体、球体中的接、切问题,通常是作出轴截面,转化为平面问题来求解.
![]()
[跟进训练]
2.圆台的上、下底面半径分别是10 cm和20 cm,它的侧面展开图的扇环的圆心角是180°,那么圆台的表面积是多少?
[解] 如图所示,设圆台的上底面周长为c,因为扇环的圆心角是180°,
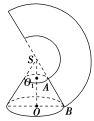
故c=π·SA=2π×10,
所以SA=20(cm),同理可得SB=40(cm),
所以AB=SB-SA=20(cm),
所以S表面积=S侧+S上+S下
=π(r1+r2)·AB+πr+πr
=π(10+20)×20+π×102+π×202=1 100π(cm2).
故圆台的表面积为1 100π cm2.
![]() 类型3 空间图形侧面积和全面积的实际应用
类型3 空间图形侧面积和全面积的实际应用
【例3】 用油漆涂100个圆台形水桶(桶内、外侧都要涂),桶口直径为30 cm,桶底直径为25 cm,母线长是27.5 cm,已知每平方米需要油漆150 g,共需要多少油漆?(精确到0.1 kg)
[解] 每个水桶需要涂油漆的面积为S=(S桶底+S侧)×2
=π×2
=0.182 5π(m2),
因此100个水桶需要油漆100×0.182 5π×0.15≈8.6(kg).
![]()
对于有关空间图形侧面积和全面积的实际问题,求解的关键是把题设信息数学化,然后借助数学知识解决该问题.
![]()
[跟进训练]
3.一个正三棱台的两底面的边长分别为8 cm、18 cm,侧棱长是13 cm,求它的全面积.
[解] 上底面周长为c′=3×8=24(cm),
下底面周长c=3×18=54(cm),
斜高h′==12(cm),
所以S正棱台侧=(c+c′)h′=×(24+54)×12=468(cm2),
S上底面=×82=16(cm2),
S下底面=×182=81(cm2),
所以正三棱台的全面积为
S=468+16+81=468+97 cm2.
![]()
1.圆台的上、下底面半径分别是3和4,母线长为6,则其表面积等于( )
A.42π B.51π C.58π D.67π
D [S圆台表=S圆台侧+S上底+S下底=π(3+4)×6+π×32+π×42=67π.]
2.在如图所示的斜截圆柱中,已知圆柱底面的直径为40 cm,母线长最短50 cm,最长80 cm,则斜截圆柱的侧面面积S=( )
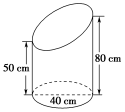
A.2 600 cm2 B.5 200 cm2
C.2 600π cm2 D.5 200π cm2
C [几何体的50 cm到80 cm处的截去的部分的面积和余下的面积相等,将几何体侧面展开,上部分面积为×40π,下部分的面积为50×40 π,由此可知,斜截圆柱的侧面面积S=50×40π+×40π=2 600π,故选C.]
3.圆锥的母线长是4,侧面积是4π,则该圆锥的高为( )
A. B.4 C.3 D.2
A [设圆锥的母线长l=4,底面半径为r,高为h,则πrl=4π,解得r=1,所以h===.故选A.]
4.一个圆柱的底面面积是S,其侧面积展开图是正方形,那么该圆柱的侧面积为________.
4πS [设圆柱的底面半径为R,则S=πR2,R=,底面周长c=2πR.故圆柱的侧面积为S圆柱侧=c2=(2πR)2=4π2=4πS.]
5.一座仓库的屋顶呈正四棱锥形,底面的边长为2.7 m,侧棱长为2.3 m,如果要在屋顶上铺一层油毡纸,则需多少油毡纸?(精确到0.1 m2)
[解] 如图所示,设SE是侧面三角形ABS的高,则SE就是正四棱锥的斜高.
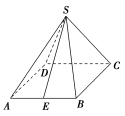
在Rt△SAE中,SA=2.3 m,AE=1.35 m,
所以SE=≈1.86(m),而底面周长=4×2.7=10.8(m),
所以S棱锥侧≈×10.8×1.86≈10.0(m2).
故需要油毡纸约10.0 m2.
![]()
回顾本节知识,自我完成以下问题:
1.空间几何体的侧面展开图与侧面积之间存在什么关系?
[提示] 相等.
2.圆柱、圆锥、圆台的侧面积公式之间存在怎样的联系?
[提示]

3.旋转体的表面积问题通常借助哪些量求解?在求解时常化归到哪些图形中?
[提示] 旋转体的表面积问题常借助底面半径、母线长及高求解,求解时常借助轴截面化归到等腰三角形、矩形或等腰梯形中求解.
![]()