【同步学案】苏教版（2019） 高中数学 第14章统计学案含解析

14.4　用样本估计总体

14.4.1　用样本估计总体的集中趋势参数

知识点　平均数、众数与中位数的定义

(1)平均数：一组数据的和除以数据个数所得到的数．把总体中所有数据的算术平均数称为总体的均值．

(2)众数：一组数据中出现次数最多的数．

(3)中位数：一组数据按照从小到大的顺序排列后，如果数据的个数为奇数，处于正中间位置的数．如果数据的个数是偶数，则取正中间两个数据的平均数．

(1)中位数一定是样本数据中的一个数吗？

(2)一组数据可以有几个众数？中位数是否也具有相同的结论？

[提示]　(1)不一定．一组数据按大小顺序排列后，如果有奇数个数据，处于中间位置的数是中位数；如果有偶数个数据，则取中间两个数据的平均数是中位数．

(2)一组数据中可能有一个众数，也可能有多个众数，中位数只有唯一一个．

1．一组样本数据为：19,23,12,14,14,17,10,12,18,14,27，则这组数据的众数和中位数分别为(　　)

A．14,14  B．12,14  C．14,15.5  D．12,15.5

A　[把这组数据按从小到大排列为：10,12,12,14,14,14,17,18,19,23,27，则可知其众数为14，中位数为14．]

2．已知一组数据4,6,5,8,7,6，那么这组数据的平均数为________．

6　[＝6．]

类型1　平均数、中位数和众数的计算

【例1】　已知10名工人生产同一零件，生产的件数分别是16,18,15,11,16,18,18,17,15,13，设其平均数为a，中位数为b，众数为c，则有(　　)

A．a＞b＞c   B．a＞c＞b

C．c＞a＞b　　  D．c＞b＞a

D　[由题意得a＝(16＋18＋15＋11＋16＋18＋18＋17＋15＋13)＝＝15.7，中位数为16，众数为18，则b＝16，c＝18，∴c＞b＞a．]

1求样本数据的中位数和众数时，把数据按照从小到大的顺序排列后，按照其求法进行.

2求样本数据的平均数的难点在于计算的准确性.

[跟进训练]

1．某学习小组在一次数学测验中，得100分的有1人，95分的有1人，90分的有2人，85分的有4人，80分和75分的各1人，则该小组成绩的平均数、众数、中位数分别是(　　)

A．85分、85分、85分   B．87分、85分、86分

C．87分、85分、85分   D．87分、85分、90分

C　[由题意知，该学习小组共有10人，因此众数和中位数都是85，平均数为＝87．]

类型2　平均数、中位数和众数的实际应用

【例2】　下面是某快餐店所有工作人员一月的收入表(单位：元)：

(1)计算所有人员的月平均收入；

(2)这个平均收入能反映打工人员的月收入的一般水平吗？为什么？

(3)去掉老板收入后，再计算平均收入，这能代表打工人员的月收入的水平吗？

[解]　(1)周平均收入1＝(30 000＋4 500＋3 500＋4 000＋3 200＋3 200＋4 100)＝7 500(元)．

(2)这个平均收入不能反映打工人员的月收入水平，可以看出打工人员的收入都低于平均收入，因为老板收入特别高，这是一个异常值，对平均收入产生了较大的影响，并且他不是打工人员．

(3)去掉老板的收入后的月平均收入2＝(4 500＋3 500＋4 000＋3 200＋3 200＋4 100)＝3 750(元)．

这能代表打工人员的月收入水平．

利用样本数字特征进行决策时的两个关注点

(1)平均数与每一个数据都有关，可以反映更多的总体信息，但受极端值的影响大；中位数是样本数据所占频率的等分线，不受几个极端值的影响；众数只能体现数据的最大集中点，无法客观反映总体特征．

(2)当平均数大于中位数时，说明数据中存在许多较大的极端值．

[跟进训练]

2．某工厂人员及月工资构成如下：

(1)指出这个表格中月工资的众数、中位数、平均数；

(2)这个表格中，平均数能客观地反映该工厂的月工资水平吗？为什么？

[解]　(1)由表格可知，众数为2 000元．

把23个数据按从小到大(或从大到小)的顺序排列，排在中间的数应是第12个数，其值为2 200，故中位数为2 200元．

平均数为69 000÷23＝3 000(元)．

(2)虽然平均数为3 000元，但由表格中所列出的数据可见，只有经理的工资在平均数以上，其余人的工资都在平均数以下，故用平均数不能客观真实地反映该工厂的工资水平．

类型3　由频率直方图求平均数、中位数和众数

【例3】　某校从参加高二年级学业水平测试的学生中抽出80名学生，其数学成绩(均为整数)的频率直方图如图所示．

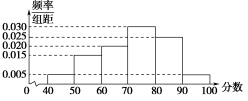
(1)求这次测试数学成绩的众数；

(2)求这次测试数学成绩的中位数．

1最高的小长方形的底边中点的横坐标即为样本数据的众数；

2判断中位数所在的区间，设出中位数，根据中位数的左右两边的频率相等列出方程求解.

[解]　(1)由题干图知众数为＝75．

(2)由题干图知，设中位数为x，由于前三个矩形面积之和为0.4，第四个矩形面积为0.3,0.3＋0.4>0.5，因此中位数位于第四个矩形内，得0.1＝0.03(x－70)，所以x≈73.3．

众数、中位数、平均数与频率直方图的联系

(1)众数：众数在样本数据的频率直方图中，就是最高矩形的底边中点的横坐标．

(2)中位数：在样本中，有50%的个体大于或等于中位数，因此，在频率直方图中，中位数左边和右边的直方图的面积应该相等，由此可估计中位数的值．

(3)平均数：用频率直方图估计平均数时，平均数等于频率直方图中每个小矩形的面积乘以每个小矩形底边中点的横坐标之和．

[跟进训练]

3．某中学举行电脑知识竞赛，现将高一参赛学生的成绩进行整理后分成五组绘制成如图所示的频率直方图，已知图中从左到右的第一、二、三、四、五小组的频率分别是0.30，0.40,0.15,0.10,0.05．

求：(1)高一参赛学生成绩的众数、中位数；

(2)高一参赛学生的平均成绩．

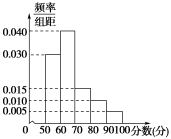
[解]　(1)用频率直方图中最高矩形所在的区间的中点值作为众数的近似值，得众数为65，又∵第一个小矩形的面积为0.3，前两个小矩形的面积和为0.3＋0.4＝0.7>0.5，设第二个小矩形底边的一部分长为x，则x×0.04＝0.2，得x＝5，∴中位数为60＋5＝65．

(2)依题意，平均成绩为55×0.3＋65×0.4＋75×0.15＋85×0.1＋95×0.05＝67，所以平均成绩约为67分．

1．一组观察值4,3,5,6出现的次数分别为3,2,4,2，则样本平均值为(　　)

A．4.55  B．4.5  C．12.5  D．1.64

A　[由条件得＝(4×3＋3×2＋5×4＋6×2)≈4.55．]

2．下列数字特征一定会在原始数据中出现的是(　　)

A．众数  B．中位数  C．平均数  D．都不会

A　[众数是在一组数据中出现次数最多的数，所以一定会在原始数据中出现．]

3．某校从高一年级参加期末考试的学生中抽出60名，其成绩(均为整数)的频率直方图如图所示，由此估计此次考试成绩的中位数、众数分别是(　　)

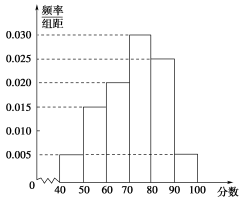
A．73.3,75  B．73.3,80  C．70,70  D．70,75

A　[由题图可知小于70分的有24人，大于80分的有18人，则在[70,80)之间的有18人，所以中位数落在[70,80)这组内，且为70＋≈73.3；众数就是频率直方图中最高的矩形底边中点的横坐标，即＝75．]

4．某高校有甲、乙两个数学建模兴趣班．其中甲班有40人，乙班有50人．现分析两个班的一次考试成绩，算得甲班的平均成绩是90分，乙班的平均成绩是81分，则该校数学建模兴趣班的平均成绩是________分．

85　[＝＝85．]

5．某校女子篮球队7名运动员身高(单位：cm)的数据分别为：171,172,17x,174,175,180,181，已知记录的平均身高为175 cm，但记录中有一名运动员身高的末位数字不清晰，如果把其末位数字记为x，那么x的值为________．

2　[170＋×(1＋2＋x＋4＋5＋10＋11)＝175，

×(33＋x)＝5，即33＋x＝35，解得x＝2．]

回顾本节知识，自我完成以下问题：

1．众数、中位数和平均数在分析样本数据时各有何优缺点？

[提示]　

2．众数、中位数、平均数与频率直方图存在怎样的关系？

[提示]　(1)平均数：在频率直方图中，样本平均数可以用每个小矩形底边中点的横坐标与小矩形的面积的乘积之和近似代替．

(2)中位数：在频率直方图中，中位数左边和右边的直方图的面积应该相等．

(3)众数：众数是最高小矩形底边的中点所对应的数据．