


高中数学人教A版 (2019)必修 第一册第三章 函数概念与性质3.2 函数的基本性质学案
展开![]() 函数奇偶性讲义(含解析答案)
函数奇偶性讲义(含解析答案)
知识点梳理
一 奇偶性的定义
(1) 一般地,如果对于函数![]() 定义域内任意一个
定义域内任意一个![]() ,都有
,都有![]() =
= ![]() ,则函数
,则函数![]() ;
;
(2) 一般地,如果对于函数![]() 定义域内任意一个
定义域内任意一个![]() ,都有
,都有![]() =
=![]()
![]() ,则函数
,则函数![]() ;
;
对于奇偶性的理解
(1) 函数的奇偶性是相对于函数的定义域而言的(整体性质);
(2) 函数的奇偶性的前提条件是定义域必须关于原点对称;
(3) 定义域关于原点对称的奇函数,则![]() =0;
=0;
(4) 既是奇函数又是偶函数的函数一定是![]() =0(定义域关于原点对称)
=0(定义域关于原点对称)
例题1 下列说法正确的是( )
- 偶函数的图像一定与
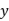 轴相交。
轴相交。 - 若奇函数
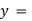
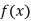 在
在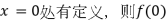 =0;
=0; - 奇函数
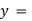
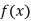 的图像一定过原点
的图像一定过原点 - 图像原点的奇函数必是单调函数
例题2 奇函数![]()
![]() (
(![]() 为奇函数,则必有( )
为奇函数,则必有( )
A. ![]()
![]()
![]()
C. ![]() <
< ![]() D
D ![]() >
> ![]()
二 奇偶函数的图像特征
(1) 奇函数的图像关于原点对称
(2) 偶函数的图像关于![]() 轴对称
轴对称
三 奇偶性和单调性的关系
奇函数在两个对称区间上的单调性相同;偶函数在两个对称区间上的单调性相反
题型一 奇偶性的判断
例题 判断下列函数的奇偶性
(1) ![]() =0
=0
(2) ![]() =2
=2
(3) ![]() =
=![]()
(4) ![]() =
=![]()
(5) ![]()
(6) ![]()
(7) ![]()
(8) ![]()
(1)既是奇函数又是偶函数(2)偶函数(3)奇函数(4)奇函数(5)既是奇函数又是偶函数(6)既不是奇函数又不是偶函数(7)偶函数(8)奇函数
题型二 利用奇偶性求解析式
例 已知![]() 是定义在R上的奇函数,当
是定义在R上的奇函数,当![]() +5,求函数的解析式
+5,求函数的解析式
解:当![]() 时,
时,![]() ,
,![]() +5=
+5= ![]() +5,
+5,
又因为![]() 是定义在R上的奇函数所以
是定义在R上的奇函数所以![]()
所以![]() =
= ![]() +5,
+5,
所以![]() =
= ![]()
![]() 5
5
由![]() 是定义在R上的奇函数可知
是定义在R上的奇函数可知![]() =0
=0
综上所述函数![]() 的解析式为
的解析式为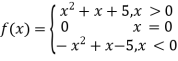
例题 已知![]() 分别是定义在R上的偶函数和奇函数,且
分别是定义在R上的偶函数和奇函数,且![]() ,求
,求![]() 的解析式
的解析式
解:由![]() 得
得![]() =
=![]()
又![]() 分别是定义在R上的偶函数和奇函数
分别是定义在R上的偶函数和奇函数
所以![]() =
= ![]() ,
,![]() =
= ![]()
所以![]() =
=![]()
联立![]()
可得![]()
![]()
题型三 奇偶性的应用
例题 已知奇函数![]()
![]() 在(0,
在(0,![]() 单调递减,且
单调递减,且![]() 则不等式
则不等式![]() 的解集为____________
的解集为____________
解:因为奇函数![]()
![]() 在(0,
在(0,![]() 单调递减,且
单调递减,且![]() ,所以奇函数
,所以奇函数![]()
![]() 在(-
在(-![]() ,且
,且![]()
所以当![]() 或
或![]() 当
当![]() 或
或![]()
当![]() 时,不等式
时,不等式![]() 等价于
等价于![]() ,
,
所以![]() 或
或![]() ,解得
,解得![]()
当![]() 时,不等式
时,不等式![]() 等价于
等价于![]() ,
,
所以![]() 或
或![]() ,解得0<
,解得0<![]()
综上不等式![]() 的解集为
的解集为![]()
例题二
已知![]() 是定义在R上的偶函数,当
是定义在R上的偶函数,当![]() 时单调递增,比较
时单调递增,比较![]()
解:因为![]() 是定义在R上的偶函数,所以
是定义在R上的偶函数,所以![]()
又2<3<![]()
![]() 时单调递增,
时单调递增,![]()
练习
一 选择题
1.若函数![]() 则下列函数为奇函数的是( )
则下列函数为奇函数的是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
2. 若奇函数![]()
![]() 在区间[3,6]上单调递增,且在区间[3,6]上的最大值为7,最小值为
在区间[3,6]上单调递增,且在区间[3,6]上的最大值为7,最小值为![]() 则
则![]() 的值为( )
的值为( )
3.已知函数![]()
![]() 为偶函数,则下列关系一定成立的是( )
为偶函数,则下列关系一定成立的是( )
A. ![]() =
= ![]() B.
B. ![]() =
= ![]()
C. ![]() =
= ![]() D.
D. ![]() =
= ![]()
4已知![]() 是奇函数,
是奇函数,
则![]() 的值( )
的值( )
- 随
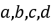 的取值而变化
的取值而变化 - 只与
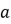 的取值有关
的取值有关 - 与
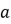 和
和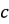 的取值都有关
的取值都有关 - 为0
5.已知定义域为R的函数![]() 在区间[2,+
在区间[2,+![]() 上单调递减,
上单调递减,
C. ![]() D.
D. ![]()
6. 已知![]() 分别是定义在R上的奇函数和偶函数,则下列结论正确的是( )
分别是定义在R上的奇函数和偶函数,则下列结论正确的是( )
A. ![]() 是偶函数
是偶函数
B.![]() 是奇函数
是奇函数
C. ![]() 是奇函数
是奇函数
D. ![]() 是奇函数
是奇函数
7.已知![]() 设函数
设函数![]() 为
为![]() 为
为![]() 则
则![]() 的值可能为( )
的值可能为( )
8.若![]() 则满足
则满足![]() 的实数
的实数![]() 的取值范围是( )
的取值范围是( )
A.(![]() B. .(
B. .(![]()
C.![]() D.
D.![]()
9.(多选题)已知![]() 指不超过
指不超过![]() 的最大整数),下列说法正确的是( )
的最大整数),下列说法正确的是( )
A.![]()
B. ![]() 为增函数
为增函数
C.![]() 为奇函数
为奇函数
D.![]()
![]()
二.填空题
1.已知定义在[![]() 的奇函数
的奇函数![]()
2.已知 ![]() 是定义在R上的奇函数,且当
是定义在R上的奇函数,且当![]() 若
若![]()
3.设![]() 是偶函数,当
是偶函数,当![]() 则使
则使![]() 的
的![]() 的取值范围是________
的取值范围是________
4.已知定义在R上的偶函数![]()
![]() 在(0,
在(0,![]() 单调递增,且
单调递增,且![]() 则不等式
则不等式![]() 的解集为____________
的解集为____________
二解答题
- 已知函数
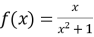
(1) 写出函数![]() 的定义域,判断并证明函数
的定义域,判断并证明函数![]() 的奇偶性;
的奇偶性;
(2) 用单调性定义证明![]() 在区间(
在区间(![]() 1,1)上单调递增;
1,1)上单调递增;
(3) 若函数![]() 的定义域为(
的定义域为(![]() 1,1),解不等式
1,1),解不等式![]()
- 定义在R上的奇函数
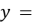
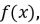 对于任意
对于任意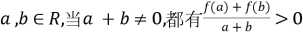
(1) 若![]() 试比较
试比较![]() 的大小关系;
的大小关系;
(2) 若![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
答案
选择题
1.A 2.B 3.B 4.D 5.D 6.C 7.B 8.C 9.AD
填空题
1. ![]() 8
8
2. ![]() 11
11
3. ![]()
4. ![]()
解答题
1(1)定义域为R,奇函数(2)略(3)(0,![]()
2(1) ![]()
(2) ![]()
高中数学人教A版 (2019)必修 第一册4.3 对数学案: 这是一份高中数学人教A版 (2019)必修 第一册4.3 对数学案,共4页。
高中数学人教A版 (2019)必修 第一册3.3 幂函数导学案及答案: 这是一份高中数学人教A版 (2019)必修 第一册3.3 幂函数导学案及答案,共7页。学案主要包含了幂函数的概念,五个幂函数的图象与性质,幂函数性质的应用等内容,欢迎下载使用。
高中数学人教A版 (2019)必修 第一册第三章 函数概念与性质3.2 函数的基本性质导学案及答案: 这是一份高中数学人教A版 (2019)必修 第一册第三章 函数概念与性质3.2 函数的基本性质导学案及答案,共3页。学案主要包含了教学目标,教学重点、难点,教学过程等内容,欢迎下载使用。













