初中数学浙教版八年级上册1.1 认识三角形精品第二课时教案

这是一份初中数学浙教版八年级上册1.1 认识三角形精品第二课时教案，共9页。教案主要包含了创设情景，引出课题等内容，欢迎下载使用。
浙教版数学八年级上册 1.1认识三角形（第二课时）教案《三角形的中线，高线，角平分线 》一、教材分析三角形是几何图形部分的重要内容之一，帮助学生了解三角形的定义，性质，定理等内容，是对简单的平面图形的进一步研究，也是后续研究多边形的性质，三角函数等知识的基础，在平面几何中有着非常重要的地位和作用。 二、学情分析首先是学生的知识特征，八年级的学生已经学习过点，直线，角的相关概念，对边和角的分类有一定了解，有能力学习三角形的概念和性质。但是学生对数学语言的理解还有待提高，三角形的中线，高线，角平分线的定义与性质在以后的中练习中经常会涉及，需要老师积极引导。然后是学生的心理特征，八年级的学生好奇心重，求知欲强，教师通过合适的方法引入有助于他们更好地三角形的相关内容。 三、教学目标知识与技能1．了解三角形的角平分线、中线、高线的概念．2．会利用量角器、刻度尺画三角形的角平分线、中线和高线．3．会利用三角形的角平分线、中线和高线的概念，解决有关角度、面积计算等问题过程与方法：在探究实践做培养学生自主学习、合作交流的能力情感态度与价值观：能用所学知识解决生活实际问题，感受数学与生活的紧密联系 四、教学重难点重点：能画出任意三角形的角平分线、中线和高难点：探究，发现三角形的角平分线、中线和高的性质 五、教学方法、手段教学方法：讲授法，讨论法，练习法教学手段：板书与多媒体课件相结合 六．教学过程一、创设情景，引出课题回顾旧知 我们以前学过角平分线，角平分线的定义是什么呢？从一个角的顶点引出的一条射线，把这个角分成两个相等的角。这条射线叫做这个角的平分线。你知道怎么做一个角的角平分线吗？用量角器或折纸的办法如图，记作∠AOC=∠BOC= ∠AOB.一个角有平分线，三角形也是有平分线的 讲授新课 在三角形中，一个内角的角平分线与它的对边相交，这个角的顶点与交点之间的线段叫做三角形的角平分线.   如图∠BAC的平分线交BC于点D,线段AD就是△ABC的一条角平分线.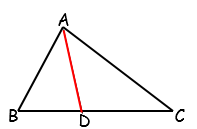∵ AD是 △ ABC的 角平分线∴ ∠BAD =∠CAD =  ∠BAC小结：三角形的角平分线与角的平分线有什么区别与联系？共同点：它们都把一个角平分成两个相等的角 不同点：角平分线是一条射线，三角形的角平分线是一条线段   练习1:（1）任意剪一个三角形，用折叠的方法（如图），画出这个三角形的三条角平分线，你发现了什么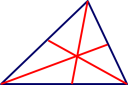？              三角形的三条角平分线交于同一点.称之为三角形的内心．（2）如图，在△ABC中，∠BAD=∠DAE=∠EAF=∠FAC，则  AE     是△ABC的角平分线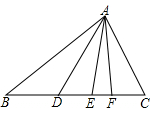． 讲授新课   任意画一个三角形，用刻度尺画出BC的中点D，连接AD。  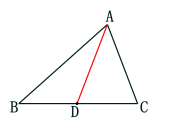  在三角形中，连接一个顶点与它对边中点的线段，叫做这个三角形的中线∵AD是△ ABC的 中线∴BD = CD =  BC特点：（1）三角形的中线是一条线段；（2）三角形的中线的一端平分这条边。练习2（1）任意剪一个三角形，用折叠的方法，找出三条边的中点，画出三条中线.你发现了什么？         三角形的三条中线交于一点.称之为三角形的重心．（2）三角形的一条中线是否将这个三角形分成面积相等的两个三角形？为什么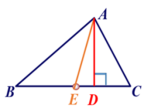？因为 S△ABE=AD×BE=    S△ACE=AD×CE=且BE=EC所以：S△ABE=S△ACE三角形的任意一条中线把这个三角形分成两个等面积等三角形，即三角形等任意一条中线平分原三角形面积。（3）填空：1.三角形一边上的中线把三角形分成的两个三角形的面积关系为______．2. 如图，当______=______时，AD是△ABC的中线；当______=______时，AD是△ABC的角平分线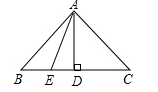．     讲授新课  已知△ ABC中，BC=3,如果要求△ ABC 的面积，还要添加什么条件？（AD⊥BC）从三角形的一个顶点向它的对边所在的直线作垂线，顶点和垂足之间的线段叫做三角形的高．如图所示，AD⊥BC于点D，AD就是△ABC的BC边上的高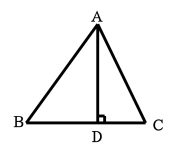．做一做 用三角尺分别作图中锐角三角形ABC,直角三角形DEF和钝角三角形PQR的各边上的高，比较这三条高线与三角形的位置关系，你发现了什么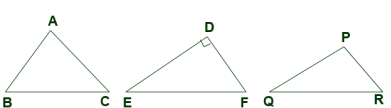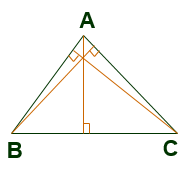？锐角三角形的三条高都在三角形内部，且三条高交于一点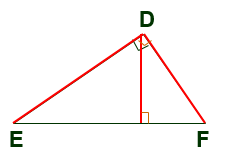直角三角形斜边上高在三角形内部，一条直角边上的高是另一条直角边，三条高相交于直角顶点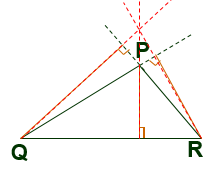钝角三角形中，夹钝角两边上的高都在三角形外部，另一条高在三角形内部，三条高的延长线也交于一点练习3:1.如果一个三角形的三条高的交点恰是三角形的一个顶点，那么这个三角形是（  B ）A.锐角三角形           B.直角三角形     C.钝角三角形           D.锐角三角形2.下列各组图形中，哪一组图形中AD是△ABC 的高(    D     )   如图，在△ABC中，AD是△ABC的高线，AE是△ABC的角平分线。已知∠BAC=80°，∠C=40 °，求∠DAE的大小。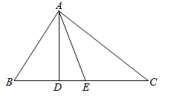解：∵ AE是△ABC 的角平分线且∠BAC=80°，∴∠EAC= ∠BAC=40°∵AD是△ABC的高线，∴∠ADC=90°根据“三角形三个内角的和等于180°”知∠DAC+∠ADC+∠C=180°，∴∠DAC=180°-∠ADC-∠C       =180°-90°-40°=50°∴∠DAE=∠DAC-∠EAC=50°-40°=10° 活动探究·1.如图，点D，E，F分别是△ABC的三条边的中点，设△ABC的面积为S，求△DEF得面积。你可以这样考虑：（1）连结AD，△ADC的面积是多少？（2）由第（1）题，你能求出△DEC的面积吗？△AEF和△FBD的面积呢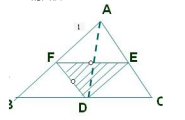？ 2.如图, D是AB的中点, E是BC的中点,F是BD的中点, 若△EFB的面积是2 ,则△ABC的面积是______16 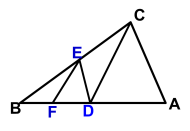当堂检测：1.三角形的高、中线与角平分线都是(  C   )    A.直线     B.射线     C.线段     D.可能是直线,也可能是线段2.如图,在△ABC中,∠ACB=90°,把△ABC沿直线AC翻折180°,使点B 落在点B′的位置,则线段AC (   D     )    A.是边BB′上的中线   B.是边BB′上的高    C.是∠BAB′的角平分线   D.以上三种性质都成立  如图，AD是△ABC的边BC上的中线，已知AB=5cm，AC=3cm．

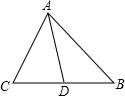
（1）求△ABD与△ACD的周长之差．
（2）若AB边上的高为2cm，求AC边上的高 4.如图所示，己知△ABC． （1）过点A画出BC边上的中线AD； （2）画出∠A的平分线AE； （3）画出AB边上的高CH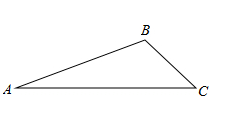． 解：（1）如图所示，AD即为所求作的中线；（2）如图所示，AE即为所求作的角平分线；（3）如图所示，CH即为所求作的AB边上的高．5.三角形的一条中线把其面积等分，把一个三角形分成面积相等的4块（至少给出两种方法）；（1）可取各边的中点顺次连接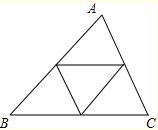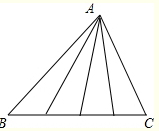；把BC四等分，让BC的四等分点分别与A连接．  6.在△ABC中,AB=AC,AC边上的中线BD把三角形的周长分为12cm和15cm两部分.求△ABC各边的长。分情况讨论：（一）周长是12cm的三角形是ABD,AB+AD=12cmBC+CD=15cm,又AD=CD=1/2AC=1/2AB所以AB+1/2AB=12 AB=8cmBC+1/2AB=15 BC+4=15 BC=11cm（二） 周长是15cm的三角形是ABD,AB+AD=15cmBC+CD=12cm,又AD=CD=1/2AC=1/2AB所以AB+1/2AB=15 AB=10cmBC+1/2AB=12 BC+5=12 BC=7cml两边之和大于第三边.两边之差小于第三边验证都成立.所以结果是：8cm 8cm 11cm或10cm 10cm 7cm 七．课堂小结，作业布置小结：本节课学习了：1.三角形的角平分线定义与性质2.三角形的高定义与性质3.三角形的中线定义与性质作业：课本P9页 4,5题，配套练习