沪科版 初中数学 九年级上册 第21章 二次函数与反比例函数单元测试卷（较易）（含答案）

这是一份沪科版 初中数学 九年级上册 第21章 二次函数与反比例函数单元测试卷（较易）（含答案），共19页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

学校:___________姓名：___________班级：___________考号：___________
第I卷（选择题）
一、选择题（本大题共12小题，共36分）
当函数y=(a−1)x2+bx+c是二次函数时，a的取值为( )
A. a=1B. a=−1C. a≠−1D. a≠1
当函数y=(a−1)xa2+1+2x是二次函数时，a的取值为( )
A. a=1B. a=±1C. a≠1D. a=−1
已知a，b是非零实数，|a|>|b|，在同一平面直角坐标系中，二次函数y1=ax2+bx与一次函数y2=ax+b的大致图象不可能是( )
A. B.
C. D.
如果将抛物线y=5x2向上平移1个单位，那么所得新抛物线的表达式是( )
A. y=5(x+1)2B. y=5(x−1)2C. y=5x2+1D. y=5x2−1
已知y=ax2+bx+c(a≠0)的图象如图所示，对称轴为直线x=2.若x1，x2是一元二次方程ax2+bx+c=0(a≠0)的两个根，且x1A. x1+x2<0
B. 4C. b2−4ac<0
D. ab>0
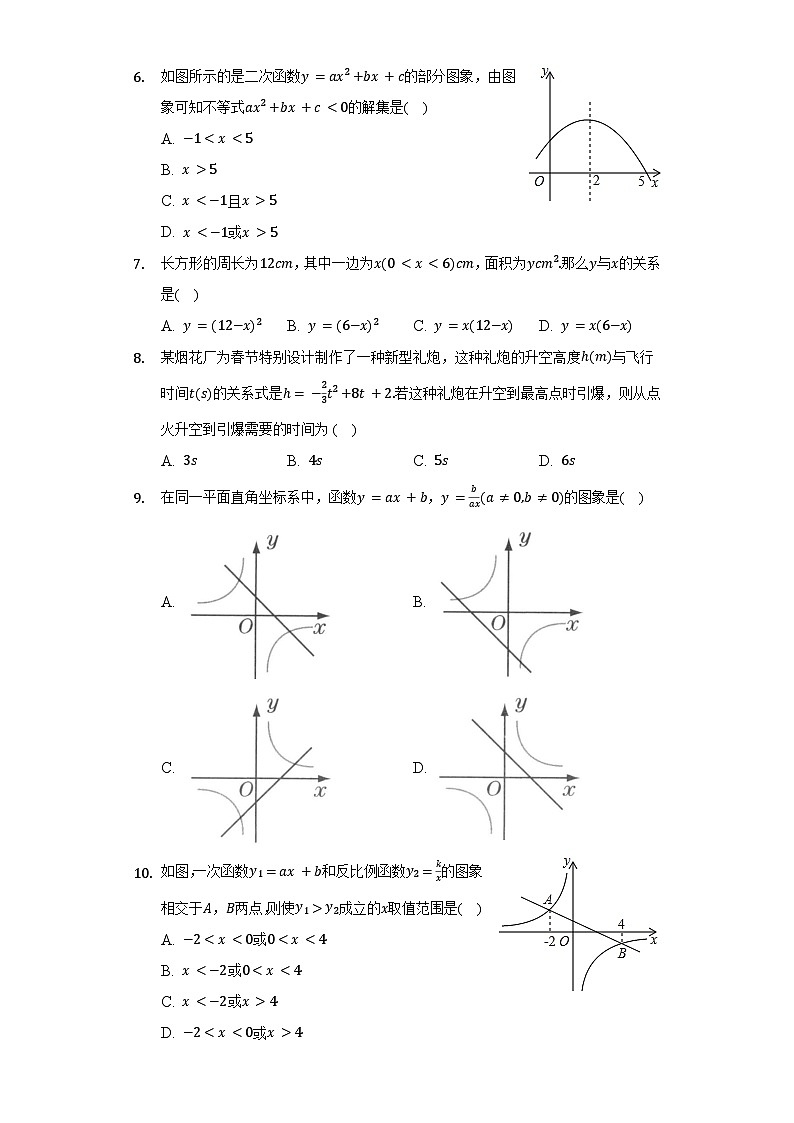
如图所示的是二次函数y=ax2+bx+c的部分图象，由图象可知不等式ax2+bx+c<0的解集是( )
A. −1B. x>5
C. x<−1且x>5
D. x<−1或x>5
长方形的周长为12cm，其中一边为x(0A. y=(12−x)2B. y=(6−x)2C. y=x(12−x)D. y=x(6−x)
某烟花厂为春节特别设计制作了一种新型礼炮，这种礼炮的升空高度ℎ(m)与飞行时间t(s)的关系式是ℎ= −23t2+8t+2.若这种礼炮在升空到最高点时引爆，则从点火升空到引爆需要的时间为( )
A. 3sB. 4sC. 5sD. 6s
在同一平面直角坐标系中，函数y=ax+b，y=bax(a≠0,b≠0)的图象是( )
A. B.
C. D.
如图，一次函数y1=ax+b和反比例函数y2=kx的图象相交于A，B两点，则使y1>y2成立的x取值范围是( )
A. −2B. x<−2或0C. x<−2或x>4
D. −24
对于函数y=−3(x+ℎ)2+k的图象，下列说法不正确的是( )
A. 开口向下B. 对称轴是直线x=−ℎ
C. 最大值为kD. 与y轴不相交
小明在期末体育测试中掷出的实心球的运动路线呈抛物线形．若实心球运动的抛物线的解析式为y=−19(x−3)2+k，其中y是实心球飞行的高度，x是实心球飞行的水平距离．已知该同学出手点A的坐标为(0,169)，则实心球飞行的水平距离OB的长度为( )
A. 7mB. 7.5mC. 8mD. 8.5m
第II卷（非选择题）
二、填空题（本大题共4小题，共12分）
已知二次函数y=ax2+3ax+a2+1.当x=1时，函数y有最大值6，则二次函数的表达式为______．
某工厂今年八月份医用防护服的产量是50万件，计划九月份和十月份增加产量，如果月平均增长率为x，那么十月份医用防护服的产量y(万件)与x之间的函数表达式为 ．
若点P(m,n)在二次函数y=x2+2x+2的图象上，且点P到y轴的距离小于2，则n的取值范围是______．
若关于x的函数y=2−ax2−x是二次函数，则a的取值范围是____．
三、解答题（本大题共9小题，共72分）
已知函数y=−(m+2)xm2−2(m为常数)，求当m为何值时：
(1)y是x的一次函数？
(2)y是x的二次函数？并求出此时纵坐标为−8的点的坐标．
一件商品原价100元，连续两次降价后(降价率相同)，售价是y元，写出y与降价率x的函数解析式．
在平面直角坐标系xOy中，已知抛物线y=−12x2+bx+c经过点A(−1,0)和点B(0,52)，顶点为C．
(1)求这条抛物线的表达式和顶点C的坐标．
(2)点D在这条抛物线的对称轴上，当DC=DA时，求点D的坐标．
已知二次函数y=mx2−(m+n)x+n(m<0)，A(−1,0)，B(0,−1)，C(0,1)．
(1)若二次函数的图象经过A，B两点，求二次函数的解析式；
(2)若二次函数图象与y轴正半轴有交点，试判断二次函数的图象与x轴的交点个数，并说明理由；
(3)若二次函数图象经过点C，设P(a,b)为二次函数图象上的一个动点，当−3如图，将边长为4的正方形ABCD折叠，使点B落在边AD上，记作B′(不与A、D重合)，EF为折痕，设AB′=x，BE=y，求出y关于x的函数关系式，并写出自变量x的取值范围．
如图所示，制作一种产品的同时，需要将原材料加热，设该材料温度为y℃，从加热开始计算的时间为x分钟，据了解，该材料在加热过程中温度y与时间x成一次函数关系，已知该材料在加热前的温度为10℃，加热5分钟使材料温度达到20℃时停止加热．停止加热后，过一段时间，材料温度逐渐下降，这时温度y与时间x成反比例函数关系．
(1)分别求出该材料加热过程中和材料温度逐渐下降过程中，y与x之间的函数表达式，并写出x的取值范围；
(2)根据工艺要求，在材料温度不低于16℃的这段时间内，需要对该材料进行特殊处理，那么对该材料进行特殊处理所用的时间是多少？
如图，在矩形ABCD的场地内，修建横竖两条甬道，场地其余部分种植草坪，已知竖向甬道的宽度是横向甬道宽度的2倍，AD=20米，AB=16米，设横向甬道的宽度为x米，草坪面积为y米 2．
(1)请写出y与x之间的函数关系式；(不必写出自变量的取值范围)
(2)若草坪面积为270米 2，请求出横向甬道的宽度．
对于向上抛的物体，如果空气阻力忽略不计，有下面的关系式：ℎ=x0t−12gt2(ℎ是物体离起点的高度，v0是初速度，g是重力系数，取10m/s2，t是抛出后经过的时间).杂技演员抛球表演时，以10m/s的初速度把球向上抛出．
(1)球抛出后经多少秒回到起点？
(2)几秒后球离起点的高度达到1.8m？
(3)球离起点的高度能达到6m吗？请说明理由．
神农尝百草，泡泡青菜便是其中之一，小随同学利用假期开网店批发出售泡泡青菜，他打出促销广告：最优质泡泡青菜35箱，每箱售价30元，若一次性购买不超过10箱时，售价不变；若一次性购买超过10箱时，每多买1箱，所买的每箱泡泡青菜的售价均降低0.3元．已知该青菜成本是每箱20元，若不计其他费用，设顾客一次性购买泡泡青菜x(x为整数)箱时，该网店从中获利y元．
(1)求y与x的函数关系式，并写出自变量x的取值范围；
(2)顾客一次性购买多少箱时，该网店从中获利最多，最多是多少？
答案和解析
1.【答案】D
【解析】
【分析】
本题主要考查二次函数的定义，熟练掌握形如y=ax2+bx+c(a、b、c是常数，a≠0)的函数，叫做二次函数是解题的关键．
根据二次函数的定义列不等式求解即可．
【解答】
解：∵函数y=(a−1)x2+bx+c是二次函数，
∴a−1≠0，
解得a≠1．
故选D．
2.【答案】D
【解析】
【分析】
本题考查二次函数的定义．
由二次函数的定义可知自变量的最高指数为2，且系数不等于0，列出方程与不等式解答即可．
【解答】
解：由题意，得 a2 +1=2且a−1 ≠ 0，解得a=−1．
故选D．
3.【答案】D
【解析】
【分析】
本题考查二次函数的图象与系数的关系、一次函数的图象与系数的关系，解题的关键是明确二次函数与一次函数图象的特点．
根据二次函数y=ax2+bx与一次函数y=ax+b(a≠0)可以求得它们的交点坐标，然后根据一次函数的性质和二次函数的性质，由函数图象可以判断a、b的正负情况，从而可以解答本题．
【解答】
解：y=ax2+bxy=ax+b解得x=−bay=0或x=1y=a+b．
故二次函数y=ax2+bx与一次函数y=ax+b(a≠0)在同一平面直角坐标系中的交点在x轴上为(−ba,0)或点(1,a+b)．
在A中，由一次函数图象可知a>0，b>0，二次函数图象可知，a>0，b>0，−ba<0，a+b>0，故选项A有可能；
在B中，由一次函数图象可知a>0，b<0，二次函数图象可知，a>0，b<0，−ba>0，由|a|>|b|，则a+b>0，故选项B有可能；
在C中，由一次函数图象可知a<0，b<0，二次函数图象可知，a<0，b<0，−ba<0，a+b<0，故选项C有可能；
在D中，由一次函数图象可知a<0，b>0，二次函数图象可知，a<0，b>0，由|a|>|b|，则a+b<0，故选项D不可能；
故选D．
4.【答案】C
【解析】解：将抛物线y=5x2向上平移1个单位，那么所得新抛物线的表达式是：y=5x2+1．
故选：C．
利用二次函数图象的平移规律，左加右减，上加下减，进而得出答案．
此题主要考查了二次函数图象与几何变换，正确记忆图形平移规律是解题关键．
5.【答案】B
【解析】解：∵x1，x2是一元二次方程ax2+bx+c=0的两个根，
∴x1、x2是抛物线与x轴交点的横坐标，
∵抛物线的对称轴为x=2，
∴x1+x22=2，即x1+x2=4>0，故选项A错误；
∵x1∴−1<4−x22<0，
解得：4∵抛物线与x轴有两个交点，
∴b2−4ac>0，故选项C错误；
∵抛物线开口向下，
∴a<0，
∵抛物线的对称轴为x=2，
∴−b2a=2，
∴b=−4a>0，
∴ab<0，故选项D错误；
故选：B．
利用函数图象分别得出抛物线与x轴交点的横坐标的关系，进而判断四个结论得出答案．
主要考查二次函数与一元二次方程之间的关系，会利用对称轴的值求抛物线与x轴交点的横坐标间的数量关系，以及二次函数与方程之间的转换，根的判别式的熟练运用．
6.【答案】D
【解析】
【分析】
本题考查了二次函数的性质、二次函数与x轴的交点坐标及根据交点坐标写出不等式的解集的有关知识，求出二次函数与x轴的交点坐标是解题的关键．
先根据二次函数的对称性求出二次函数与x轴的交点坐标，再根据交点坐标即可写出不等式ax2+bx+c<0的解集．
【解答】
解：由题图知抛物线的对称轴是直线x=2，与x轴的一个交点的坐标为(5,0)，
∴抛物线与x轴的另一个交点的坐标为(−1,0)，
利用图象可知ax2+bx+c<0的解集即是y<0时对应的x的取值范围，
∴不等式ax2+bx+c<0的解集是x<−1或x>5．
故选D．

7.【答案】D
【解析】解：∵长方形的周长为12cm，其中一边长为x cm，
∴另一边长为(6−x)cm，
面积y=x(6−x)，
故选：D．
由长方形的周长，可知一组邻边和，由一边长为x cm，可知另一边为(6−x)cm，则可表示面积．
本题考查了根据实际问题列二次函数关系式，理解长方形的边长、周长以及面积之间的关系是解题的关键．
8.【答案】D
【解析】∵礼炮在点火升空到最高点时引爆，
∴从点火升空到引爆需要的时间为8−2×(−23)=6 s．
9.【答案】A
【解析】
【分析】本题考查了反比例函数的图象和性质.根据一次函数的参数a和b的正负性及作用，以及反比例函数自变量系数ba的正负性可得出选项．
【解答】
解：A.y=bax可化为y=bax，A中双曲线在第二、四象限，则ba<0，a，b异号，而直线y=ax+b过第一、二、四象限，则a<0，b>0，故A正确;
B.双曲线在第二、四象限，则ba<0，a，b异号，而直线y=ax+b过第二、三、四象限，则a<0，b<0，这与a，b异号相矛盾，故B错误;
C.双曲线在第一、三象限，则ba>0，a，b同号，而直线y=ax+b过第一、三、四象限，则a>0，b<0，这与a，b同号相矛盾，故C错误;
D.双曲线在第一、三象限，则ba>0，a，b同号，而直线y=ax+b过第一、二、四象限，则a<0，b>0，这与a，b同号矛盾，故D错误．
故选A．

10.【答案】B
【解析】
【分析】
本题考查了一次函数与反比例函数综合，属于基础题．
根据函数图象，即可得解．
【解答】
解：观察函数图象可发现：当x<−2或0∴使y1>y2成立的x取值范围是x<−2或0故选：B．
11.【答案】D
【解析】解：对于函数y=−3(x+ℎ)2+k的图象，
∵a=−3<0，
∴开口向下，对称轴x=−ℎ，顶点坐标为(−ℎ,k)，函数有最大值k，与y轴的交点坐标是(0,−3ℎ2+k)，
故D选项符合题意，
故选：D．
根据二次函数的性质即可一一判断．
本题考查二次函数的性质，解题的关键是熟练掌握二次函数的性质，属于基础题，中考常考题型．
12.【答案】C
【解析】解：把A(0,169)代入y=−19(x−3)2+k得：
169=−19×9+k，
∴k=259，
∴y=−19(x−3)2+259，
令y=0得−19(x−3)2+259=0，
解得x=−2(舍去)或x=8，
∴实心球飞行的水平距离OB的长度为8m，
故选：C．
根据出手点A的坐标为(0,169)求出函数关系式，再令y=0可解得答案．
本题考查二次函数的应用，解题的关键是理解题意，能用待定系数法求出函数关系式．
13.【答案】y=−5x2−15x+26
【解析】解：∵当x=1时，函数y有最大值6，
∴a+3a+a2+1=6，
解得：a=1或−5，
∵有最大值，
∴a<0，
∴a=−5，
∴二次函数的表达式为y=−5x2−15x+26．
故答案为：y=−5x2−15x+26．
把x=1代人二次函数的解析式求得a的值即可．
本题考查了二次函数的性质等知识，解题的关键是根据题意求得a的值后进行正确的取舍，难度不大．
14.【答案】y=50(1+x)2
【解析】解：由题意知，九月份医用防护服的产量为50(1+x)万件，十月份医用防护服的产量为50(1+x)2万件，所以y与x之间的函数表达式为y=50(1+x)2．
15.【答案】−1≤n<10
【解析】解：∵y=x2+2x+2=(x+1)2+1，
∴二次函数y=x2+2x+2的图象开口象上，顶点为(−1,−1)，对称轴是直线x=−1，
∵P(m,n)到y轴的距离小于2，
∴−2而−1−(−2)<2−(−1)，
当m=2，n=(2+1)2+1=10，
当m=−1时，n=−1，
∴n的取值范围是−1≤n<10，
故答案为：−1≤n<10．
由题意可知−2本题考查二次函数的性质，解题的关键是掌握二次函数的图象及性质．
16.【答案】a≠2
【解析】
【分析】
根据二次函数的定义即可得．
本题主要考查二次函数的定义，熟练掌握形如y=ax2+bx+c(a、b、c是常数，a≠0)的函数，叫做二次函数是解题的关键．
【解答】
解：∵函数y=(2−a)x2−x是二次函数，
∴2−a≠0，即a≠2，
故答案为：a≠2．
17.【答案】解：(1)由y=−(m+2)xm2−2(m为常数)，y是x的一次函数，得
m2−2=1m+2≠0，
解得m=±3，
当m=±3时，y是x的一次函数；
(2)y=−(m+2)xm2−2(m为常数)，是二次函数，得
m2−2=2m+2≠0，
解得m=2，m=−2(不符合题意的要舍去)，
当m=2时，y是x的二次函数，
当y=−8时，−8=−4x2，
解得x=±2，
故纵坐标为−8的点的坐标的坐标是(±2,−8)．
【解析】(1)根据形如y=kx(k≠0,k是常数)是一次函数，可得一次函数；
(2)根据形如y=ax2(a是常数，且a≠0)是二次函数，可得答案，根据函数值，可得自变量的值，可得符合条件的点．
本题考查了二次函数的定义，利用了二次函数的定义，一次函数的定义，注意二次项的系数不能为零．
18.【答案】解：根据题意得，
y=100(1−x)2．
【解析】此题主要考查了根据实际问题列出二次函数解析式，解答此题注意两次降价x的标准不同，第一次x以原价为标准，第二次x以第一次降价后的价格为标准.此题的数量关系是：原价×(1−x)(1−x)=售价，设出原价，列出方程即可解答．
19.【答案】解：(1)由题意得−12−b+c=0c=52，
解得b=2c=52，
∴抛物线解析式为y=−12x2+2x+52，
∵y=−12x2+2x+52=−12(x−2)2+92，
∴顶点C的坐标为(2,92)；
(2)设直线AC为y=kx+m，
把A(−1,0)，C(2,92)代入得−k+m=02k+m=92，
解得k=32m=32，
∴直线AC为y=32x+32，
∵A(−1,0)，C(2,92)，
∴AC的中点为(12,94)，
∵DC=DA，
∴D是AC的垂直平分线上的点，
设AC的垂直平分线的解析式为y=−23x+n，
代入(12,94)得94=−23×12+n，
解得n=3112，
∴AC的垂直平分线的解析式为y=−23x+3112，
把x=2代入得y=−43+3112=54，
∴点D的坐标为(2,54)
【解析】(1)把点A(−1,0)和点B(0,52)代入y=−12x2+bx+c，利用待定系数法求抛物线解析式；
(2)先求得直线AC的解析式，根据题意求得直线AC的垂直平分线的解析式，代入x=2即可求得D的坐标．
本题考查了待定系数法求二次函数的解析式，一次函数的解析式，二次函数图象上点的坐标特征，熟知待定系数法是解题的关键．
20.【答案】解：(1)∵二次函数y=mx2−(m+n)x+n的图象经过A(−1,0)，B(0,−1)两点，
∴m+m+n+n=0n=−1，
解得m=1n=−1，
∴二次函数的解析式为：y=x2−1．
(2)二次函数的图象与x轴必有两个交点，理由如下：
令mx2−(m+n)x+n=0，
则Δ=(m+n)2−4mn=(m−n)2，
∵二次函数图象与y轴正半轴相交，
∴n>0，
又∵m<0，
∴m−n<0，
∴Δ=(m−n)2>0，
∴该二次函数的图象与x轴必有两个交点．
(3)由题意得得二次函数的解析式为：y=mx2−(m+1)x+1．
∵M(a,b) 为二次函数图象上的一个动点，
∴b=ma2−(m+1)a+1．
∴点M关于轴的对称点M′的坐标为(a,−b)．
∴M′点在二次函数y=−mx2+(m+1)x−1上．
∵当−3当a=0时，b=1；当a=−3时，b=12m+4；
结合图象可知：−(12m+4)≤2，
解得：m≥−12．
∴m的取值范围为：−12≤m<0．
【解析】(1)将点A，B两点坐标代入二次函数解析式求解即可；
(2)直接利用根的判别式，结合完全平方公式求出Δ的符号进而得出答案；
(3)根据当−3此题主要考查了二次函数综合以及根的判别式和一次函数图象的平移等知识，由二次函数的性质得出不等式是解题关键．
21.【答案】解：∵四边形ABCD是正方形，
∴∠A=90°，AB=4，
由折叠可得：
BE=BE′=y，
在Rt△AEB′中，AE2+AB′2=B′E2，
∴x2+(4−y)2=y2，
∴y=18x2+2，(0∴y关于x的函数关系式为：y=18x2+2(0【解析】根据正方形的性质可得∠A=90°，AB=4，再根据折叠的性质可得BE=BE′=y，然后在Rt△AEB′中，利用勾股定理进行计算即可解答．
本题考查了翻折变换(折叠问题)，函数关系式，函数自变量的取值范围，根据实际问题列二次函数关系式，熟练掌握折叠的性质，以及勾股定理是解题的关键．
22.【答案】解：(1)设线段AB解析式为：y=kx+b，代入(0,10)(5,20)，
b=105k+b=20，
解得：k=2b=5，
可得：y=2x+10(0≤x≤5)，
双曲线CD解析式为：y=kx(k≠0)，
∵C(10,20)，
∴k=200，
∴双曲线CD的解析式为：y=200x(10≤x≤24)；
(2)把y=16代入y=200x中，
解得：x=252，
y=16代入y=2x+10，
解得：x=3，
∴252−3=192(分钟)，
答：该材料进行特殊处理所用的时间192分钟．
【解析】(1)直接利用待定系数法分别得出一次函数与反比例函数解析式；
(2)利用y=16，分别代入解析式进而得出x的值，即可得出答案．
此题主要考查了反比例函数的应用，正确求出函数解析式是解题关键．
23.【答案】解：(1)∵竖向甬道的宽度是横向甬道宽度的2倍，横向甬道的宽度为x米，
∴竖向甬道的宽度为2x米，
∴种植草坪的部分可合成长为(20−2x)米，宽为(16−x)米的矩形，
∴草坪面积y=(20−2x)(16−x)，
即y=2x2−52x+320．
(2)依题意得：2x2−52x+320=270，
整理得：x2−26x+25=0，
解得：x1=1，x2=25(不合题意，舍去)．
答：横向甬道的宽度为1米．
【解析】(1)根据横、竖甬道宽度间的关系，可得出竖向甬道的宽度为2x米，利用矩形的面积计算公式，结合种植草坪的部分可合成长为(20−2x)米，宽为(16−x)米的矩形，即可得出y与x之间的函数关系式；
(2)根据草坪面积为270米 2，即可得出关于x的一元二次方程，解之取其符合题意的值即可得出结论．
本题考查了一元二次方程的应用以及二次函数的应用，解题的关键是：(1)根据各数量之间的关系，找出y与x之间的函数关系式；(2)找准等量关系，正确列出一元二次方程．
24.【答案】解：∵初速度为10m/s，g取10m/s2，
∴ℎ=10t−12×10t2=10t−5t2，
(1)当ℎ=0时，
10t−5t2=0，
解得t=0或t=2，
∴球抛出后经2秒回到起点；
(2)当ℎ=1.8时，
10t−5t2=1.8，
解得t=0.2或t=1.8，
∴0.2秒或1.8秒后球离起点的高度达到1.8m；
(3)球离起点的高度不能达到6m，理由如下：
若ℎ=6，则10t−5t2=6，
整理得5t2−10t+6=0，
Δ=(−10)2−4×5×6=−20<0，
∴原方程无实数解，
∴球离起点的高度不能达到6m．
【解析】(1)当ℎ=0时，10t−5t2=0，可解得球抛出后经2秒回到起点；
(2)当ℎ=1.8时，10t−5t2=1.8，可解得0.2秒或1.8秒后球离起点的高度达到1.8m；
(3)若ℎ=6，则10t−5t2=6，可得Δ=(−10)2−4×5×6=−20<0，原方程无实数解，即可知球离起点的高度不能达到6m．
本题考查二次函数的应用，解题的关键是理解题意，掌握解一元二次方程的方法．
25.【答案】解：(1)y=30x−20x(0≤x≤10)[30−0.3(x−10)−20]x=−0.3x2+13x(10(2)在0≤x≤10时，y=10x，当x=10时，y有最大值100；
在10当x=2123时，y取得最大值，
∵x为整数，根据抛物线的对称性得x=22时，y有最大值140.8．
∵140.8>100，
∴顾客一次购买22箱时，该网站从中获利最多，最多是140.8元．
【解析】(1)根据题意可得出销量乘以每台利润进而得出总利润，进而得出答案；
(2)根据销量乘以每台利润进而得出总利润，即可求出即可．
此题主要考查了二次函数的应用，根据题意得出y与x的函数关系是解题关键．