

华师大版八年级上册3 积的乘方优质导学案
展开3.积的乘方
学习目标:1.理解并掌握积的乘方法则及其应用.(重点)
2.会运用积的乘方的运算法则进行计算.(难点)
自主学习
1.计算:(1) 10×102×103 =_________;
(2) (x5)2=_________.
2.(1)同底数幂的乘法:am·an=_________( m,n都是正整数);
(2)幂的乘方:(am)n=__________(m,n都是正整数).
填一填:根据乘方的意义及乘法交换律、结合律进行计算:
 (ab)2 (ab)3
(ab)2 (ab)3
=(ab)(ab) =_____·______·____
=(aa)(bb) =_____·______
=a2b2 . =_____.
合作探究
探究点1:积的乘方运算
问题:根据以上计算过程,如果把2或3换成任意正整数n,则(ab)n=_____.
【要点归纳】积的乘方法则: (ab)n =______(n为正整数),即积的乘方,等于把积的每一个因式分别_______,再把所得的幂________.
例1计算:(1)(2ab)3; (2)-(3x2y)2; (3)(-3ab2c3)3; (4)(-xmy3m)2.
【针对训练】
1.计算(-2a2)2的结果是( )
A.2a4 B.-2a4 C.4a4 D.-4a4
- 填空:
(1)(-2xy)4=___________;(2)(3a2)n=___________.
【方法总结】运用积的乘方法则进行计算时,注意每个因式都要乘方,尤其是字母的系数不要漏乘方.
例2计算:
(1) -4xy2·(xy2)2·(-2x2)3; (2) (-a3b6)2+(-a2b4)3.
【方法总结】涉及积的乘方的混合运算,一般先算积的乘方,再算乘法,最后算加减,然后合并同类项.
【针对训练】计算:(1)(2tm)2·t; (2)(-xy2)6+(-3x2y4)3.
探究点2:积的乘方法则的逆用
例3 计算:(1)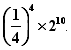 (2)
(2)![]() .
.
例4 已知(ab)m=2,bn=3,求ambm+n的值.
【方法总结】逆用积的乘方公式an·bn=(ab)n,要灵活运用,对于不符合公式的形式,要通过恒等变形,转化为公式的形式,再运用此公式可进行简便运算.
【针对训练】已知实数x,y满足x+y=2,x-y=5,不用解出x,y的值,求(x+y)13(x-y)14的值.
二、课堂小结
积的乘方 | (ab)n=___________(n是正整数). |
使用范围 | 底数是因式积的乘方. |
方法 | 把积的每一个因式分别_________,再把所得的幂___________. |
注意事项 | 运算过程,注意字母系数不要漏乘方,还应防止符号上的错误. |
当堂检测
1.计算(ab2)3的结果,正确的是( )
A.a3b6 B.a3b5 C.ab6 D.ab5
2.计算 (-x2y)2的结果是( )
A.x4y2 B.-x4y2 C.x2y2 D.-x2y2
3.下列运算正确的是( )
A.(ab3)2=ab6 B.(﹣3xy)3=﹣9x3y3
C.(-x2)3=x6 D.(3x)2=9x2
4.下面的计算对不对?如果不对,请改正过来.(将正确的答案填在横线上)
(1)(3cd)3=9c3d3; ( ) 改正:______________
(2)(-3a3)2= -9a6; ( ) 改正:______________
(3)(-2x3y)3= -8x6y3; ( ) 改正:______________
(4)(-ab2)2= a2b4. ( ) 改正:______________
5. 计算: (1) 82026×0.1252025= ________; (2) ![]() = .
= .
6.计算:
(1) (ab)8 ; (2) (2m)3; (3) (-xy)5;
(4) (5ab2 )3 ; (5) (2×102 )2; (6) (-3×103)3.
7.计算:
(1)(-2x3)3·(x2 )2 ; (2)a3·a4·a+(-2a4)2; (3)(x2y)4 +(x4y2)2.
拓展提升
8.如果(an•bm•b)3=a9b15,求m, n的值.
参考答案
自主学习
一、知识链接
1.(1)106 (2)x10
2.(1)am+n (2)amn
二、新知预习
填一填:交换 结合 (ab) (ab) (ab) (aaa) (bbb) a3 b3
合作探究
一、探究过程
探究点1:
问题: anbn
【要点归纳】anbn 乘方 相乘
例1 解:(1)原式=8a3b3. (2) 原式=-9x4y2 .
(3) 原式=-27a3b6c9. (4) 原式=x2my6m.
【针对训练】1.C 2.(1)16x4y4 (2)3na2n
例2 解:(1) 原式= 32x9y6 . (2) 原式= 0.
【针对训练】解:(1)原式=4t2m+1 .(2)原式=-26x6y12.
探究点2:
例3 解:(1)原式= 4.
4.
(2)原式=0.42019×(-0.25)2019×0.4=[0.4×(-0.25)]2019×0.4=-1×0.4=-0.4.
例4 解:ambm+n=am·bm·bn=(ab)m·bn=2×3=6.
【针对训练】解:原式=[(x+y)13(x-y)13](x-y)=[(x+y)(x-y)]13(x-y)=5×1013.
二、课堂小结
anbn 乘方 相乘
当堂检测
1.A 2.A 3.D 4.(1)× 27c3d3 (2)× 9a6 (3)× -8x9y3 (4)√
5.(1)8 (2)-3
6. 解:(1) 原式=a8b8. (2) 原式=8m3. (3) 原式=-x5y5.
(4) 原式=125a3b6. (5) 原式=4×104. (6) 原式=-27×109.
7. 解: (1)原式=-8x13. (2)原式=5a8. (3)原式=2x8y4.
8解:因为(an•bm•b)3=a9b15,所以a3n•b3m+3=a9b15,所以3n=9,3m+3=15,解得n=3,m=4.
初中数学3 反证法优秀学案及答案: 这是一份初中数学3 反证法优秀学案及答案,共4页。学案主要包含了知识链接,新知预习等内容,欢迎下载使用。
初中数学华师大版八年级上册3 边角边优秀导学案: 这是一份初中数学华师大版八年级上册3 边角边优秀导学案,共6页。学案主要包含了知识链接,新知预习等内容,欢迎下载使用。
数学1 命题优质学案设计: 这是一份数学1 命题优质学案设计,共4页。学案主要包含了知识链接,新知预习等内容,欢迎下载使用。













