华师大版 初中数学 八年级上册 13.4.4-5 尺规作图 学案(含答案)
展开13.4 尺规作图
4.经过一已知点作已知直线的垂线 5.作已知线段的垂直平分线
学习目标:
1.让学生学会利用直尺和圆规作已知直线的垂线 (重点) ;
2.让学生学会利用直尺和圆规作已知线段的垂直平分线 (难点).
自主学习
一、新知预习
1.根据上节课的知识,作平角ACB的平分线CD.问:CD与直线AB有何位置关系?
2.若A、B是直线AB上两定点,且AC=BC,AD=BD,C与D不重合.问:CD垂直平分AB吗?由此你能过直线AB上一点C作出AB的垂线吗?
合作探究
一、探究过程
探究点1:经过一已知点作已知直线的垂线
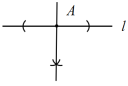
问题1 根据作平角ACB的平分线CD,试过直线l上一点A,作该直线的垂线.
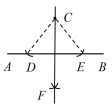
操作1 过直线AB外一点C,作直线AB的垂线.按以下步骤画图:
(1)以点C为圆心,以任意长为半径作弧,与直线AB相交于点D和点E;
(2)连接CD、CE,作∠DCE的平分线CF;
(3)作直线CF.
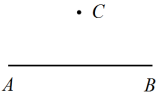
问题2 根据上述作图,说明CF⊥AB.
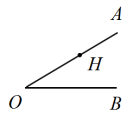
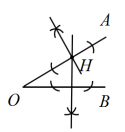
【针对训练】利用直尺和圆规,过点H作OA、OB的垂线.
探究点2:作已知线段的垂直平分线
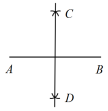
操作2 已知线段AB,按以下步骤作出线段AB的垂直平分线CD.
(1)分别以A,B为圆心,大于![]() AB的长为半径作弧,两弧交于点C和点D;
AB的长为半径作弧,两弧交于点C和点D;
(2)作直线CD.
![]()
思考1:在上述作法中,为什么要以“大于![]() AB的长”为半径作弧?
AB的长”为半径作弧?
思考2:根据上面作法中的步骤,请你说明CD为什么是AB的垂直平分线,并与同伴进行交流.
【归纳总结】可以运用线段垂直平分线的尺规作图确定线段的中点.
二、课堂小结
| 内容 |
经过一已知点作已知直线的垂线 | (1)点在直线上 (2)点在直线外 |
作已知线段的垂直平分线 |
|
当堂检测
1.尺规作图:经过已知直线外一点作这条直线的垂线,下列作图中正确的是( )
A.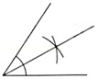 B.
B.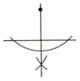 C.
C. D.
D.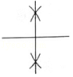
2.下列四种基本尺规作图中,作法错误的是( )
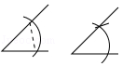
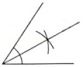
A.作一个角等于已知角 B.作一个角的平分线
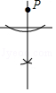
C.作一条线段的垂直平分线 D.过直线外一点P作已知直线的垂线
3.如何用尺规过直线l上一点P作已知直线l的垂线,下面作法的合理顺序为 .
①分别以A、B为圆心,以大于![]() AB的长为半径画弧,两弧相交于点C;
AB的长为半径画弧,两弧相交于点C;
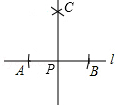 ②在直线l上点P的两旁分别截取线段PA,PB,使PA=PB;
②在直线l上点P的两旁分别截取线段PA,PB,使PA=PB;
③过点C、P作直线CP,则直线CP为所求作的直线.
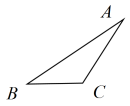
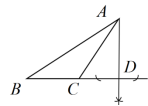
4.尺规作图(不写作法,保留作图痕迹):
如图,已知△ABC,求作△ABC的高AD.
参考答案
自主学习
一、新知预习
1.解:CD⊥AB.因为CD平分平角ACB,所以∠ACD=∠BCD=90°,即CD⊥AB.
2.解:能.连接CD.直线CD⊥AB.
合作探究
一、探究过程
探究点1
问题1 解:如图所示:
操作1 解:如图所示:
问题2 解:略
【针对训练】解:如图所示:
探究点2
操作2 解:如图所示:
思考1:解:以“小于![]() AB的长”为半径作弧没有交点;以“等于于
AB的长”为半径作弧没有交点;以“等于于![]() AB的长”为半径作弧只有一个交点,即为AB中点.
AB的长”为半径作弧只有一个交点,即为AB中点.
思考2:解:可用“SSS”证明.
二、课堂小结
直线EF
当堂检测
1.B 2.C 3.②①③
4.如图,AD即为所求.
初中数学3 反证法优秀学案及答案: 这是一份初中数学3 反证法优秀学案及答案,共4页。学案主要包含了知识链接,新知预习等内容,欢迎下载使用。
华师大版 初中数学 八年级上册 13.4.1-3 尺规作图 学案(含答案): 这是一份华师大版 初中数学 八年级上册 13.4.1-3 尺规作图 学案(含答案),共6页。学案主要包含了新知预习,课堂小结等内容,欢迎下载使用。
初中数学华师大版八年级上册3 边角边优秀导学案: 这是一份初中数学华师大版八年级上册3 边角边优秀导学案,共6页。学案主要包含了知识链接,新知预习等内容,欢迎下载使用。