数学七年级上册3 去括号与添括号精品学案设计

3. 去括号与添括号

学习目标：

1.在具体情境中体会去括号的必要性，了解去括号法则；

2.掌握去括号、添括号的法则，并能利用法则解决简单的问题（重点、难点）.

自主学习

一、知识链接

1.合并同类项：

（1）；   （2）； （3） ； （4）.

2.乘法分配律（用字母表示）：____________.

二、新知预习

（预习课本P105-109）填空并完成练习：

1.去括号法则：

（1）括号前面是“+”号，把括号和它前面的“+”号去掉，原括号里的各项都       正负号.

（2）括号前面是“-”号，把括号和它前面的“-”号去掉，原括号里的各项都       正负号.

2.添括号法则：

（1）所添括号前面是“+”号，括到括号里的各项都       正负号；

（2）所添括号前面是“-”号，括到括号里的各项都       正负号.

练习：1.去括号：

（1）a +（b-c）；      （2）（a-b）-（c-2d）.

2.添括号：

（1）a+b+c＝﹣（　            　）；

（2）2a-b+c＝2a+（　            　）；

（3）-a+b-c-2d＝-a-（　          　）．             

合作探究

一、要点探究

探究点1：去括号

问题1：回忆我们学过的加法结合律的字母式子a+（b+c）=a+b+c，你发现了什么？

【要点归纳】去括号法则：

括号前是“+”时，把括号和它前面的“+”号去掉，原括号里的各项都_________________.

问题2：若一辆公交车上原来有a人，到了一站下车b人，又到了一站下车c人，请计算最后车上的人数.

对于此题，我们有两种思路：

方法一：分别减去2次下车的人数，列式为           .

方法二：先算出2次下车的总人数，再用原来的人数减去下车的总人数，列式为           .

思考：根据上述列式，可以得到一个等式，请把该等式写出来，并说说你发现了什么？

【要点归纳】去括号法则：括号前面是“-”号，把括号和它前面的“-”号去掉，原括号里的各项都_________________.

例1   化简：

（1）－（a－b）＋（4a－2b－c）；

（2）2（2x－3y＋z）－3（4x＋y）.

【易错题醒】1.当括号前面有数字因数时，可应用乘法分配律将这个数字因数乘以括号内的每一项，切勿漏乘．

2.当含有多重括号时，可以由内向外逐层去括号，也可以由外向内逐层去括号．每去掉一层括号，若有同类项可随时合并，这样可使下一步运算简化，减少差错．

【针对训练】 化简：

（1）－(a2－4a＋3)+(5a2－a＋2)；

（2）4a2+2（3ab﹣2a2）﹣（7ab﹣1）．

例2   先化简，再求值：(3a2－ab＋7)－(5ab－4a2＋7)，其中a＝2，b＝ .

探究点2：添括号

问题   由“探究1”我们可以得到以下两个等式，观察左右调换后的式子，你发现了什么？

（1）a+（b+c）=a+b+c，左右调换后：a+b+c =a+（b+c）；

（2）a-（b+c）=a-b-c，左右调换后：a-b-c=a-（b+c）.

【要点归纳】添括号法则：

（1）所添括号前面是“+”号，括到括号里的各项都        符号；

（2）所添括号前面是“-”号，括到括号里的各项都        符号.

例3   在横线上填写恰当的项：

（1）﹣x2+x＝﹣（　            　）；

（2）3x2﹣2xy2+2y2＝3x2﹣（　            　）；

（3）﹣a3+2a2﹣a+1＝-（　            　）-（　            　）．

【针对训练】下列各式添括号错误的是（　　）

A．2a﹣b﹣x﹣3y＝2a﹣（b+x+3y） 

B．2a﹣b﹣x﹣3y＝（2a﹣b）﹣（x+3y） 

C．2a﹣b﹣x﹣3y＝﹣（x+3y）﹣（b﹣2a） 

   D．2a﹣b﹣x﹣3y＝（2a﹣3y）﹣（b﹣x）

例4   利用添括号法则计算：

（1）137x+15x-2x；    （2）156a-18a-38a.

例5   已知a+b=-7，ab=10，求代数式（3ab+6a+4b）-（2a-2ab）的值．

【方法总结】在化简时要注意去括号时是否变号；若所给的值是负数，在代入计算时要添上括号.

【针对训练】化简求值：已知2a+b=3，求代数式3（a-2b）+5（a+2b-1）-1的值．

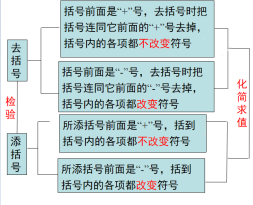
二、课堂小结

当堂检测

1.下列添括号正确的是（　　）

A．x+y＝﹣（x﹣y）  B．x﹣y＝﹣（x+y） 

C．﹣x+y＝﹣（x﹣y）  D．﹣x﹣y＝﹣（x﹣y）

2.下列去括号或添括号正确的是（　　）

A．x+（y﹣2）＝x+y+2  B．x﹣（y﹣1）＝x﹣y﹣1 

C．x﹣y+1＝x﹣（y﹣1）  D．x+y﹣1＝x+（y+1）

3.不改变代数式的值，把代数式括号前的“－”号变成“＋”号，结果应是（  ）

A．     B．     C．    D.

4.已知a-b=-3,c+d=2,则（b+c）-(a-d)的值为（   ）

A.1                B.5                 C.-5              D.-1

5.在下列各式的括号内填上适当的项．

（1）x-y-z=x+（          ）=x-（          ）；

（2）=1-（         ）；

（3）=-（        ）=-（         ）．

6.用简便方法计算：

（1） 21a+47a+53a；      （2） 214a－39a－61a.

7.化简：

 （1）；       （2）.  

8 先化简，再求值：

（1），其中a=-2；

（2）已知x2-2y-5=0，求多项式3（x2-2xy-3）-（x2-6xy+4y）的值．

参考答案

自主学习

一、知识链接

1.解：（1）原式=4a.（2）原式=.（3）原式=.（4）原式=0.

2.a（b+c）=ab+ac

二、新知预习

1.（1）不改变   （2）改变

2.（1）不改变   （2）改变

练习：1.解：（1）a +（b-c）=a +b-c.      （2）（a-b）-（c-2d）=a-b-c+2d.

2.解：（1）-a-b-c    （2）-b+c    （3）-b+c+2d     

合作探究

一、要点探究

探究点1：去括号

【要点归纳】不改变正负号

问题2   a-b-c    a-（b+c）

【要点归纳】改变正负号

例1   解：（1）原式=－a+b＋4a－2b－c=3a－b－c.

（2）原式=4x－6y＋2z－12x－3y=－8x－9y+2z.

【针对训练】解：（1）原式=4a2+3a-1.  （2）原式=﹣ab+1. 

例2   原式＝3a2﹣ab+7﹣5ab+4a2﹣7＝7a2﹣6ab，当a＝2，b＝时，原式＝28﹣4＝24.

探究点2：添括号

【要点归纳】（1）不改变  （2）改变

例3  （1）x2﹣x     （2）2xy2﹣2y2      （3）a3﹣2a2      a﹣1

【针对训练】D  

例4   解：（1）原式=137x+（15x-2x）=137x+13x=150x.

（2）原式=156a-（18a+38a）=156a-56a=100a.

例5   解：原式=3ab+6a+4b-2a+2ab=5ab+4a+4b=5ab+4（a+b）.

当a+b=-7，ab=10时，原式=5×10+4×（-7）=22．

【针对训练】解：原式=3a-6b+5a+10b-5-1=8a+4b-6=4（2a+b）-6．

因为2a+b=3，所以原式=4×3-6=6.

当堂检测

1.C   2.C   3.D    4.B

5.（1）    （2）   （3）  

6.解：（1）121a.  （2）114a.

7.解：（1）= =.        

（2）==

8.解：（1）.

将a=-2代入上式，原式.

（2）原式=3x2-6xy-9-x2+6xy-4y=2x2-4y-9=2（x2-2y）-9．

由x2-2y-5=0可得x2-2y=5，代入得：原式=10-9=1．