浙教版 初中数学 七年级上册 6.4 线段的和差 导学稿（无答案） 试卷
展开
师生共用导学稿
课题：《6.4线段的和差》 课型：新授课 时间：12月26日
班级_________ 姓名_________ 学号
一、学习目标
1、理解线段的和差的意义。
2、会用直尺和圆规作两条线段的和与差。
3、理解线段的中点的概念，会用刻度尺二等分一条线段。
4、会进行有关线段的和、差、倍、分的简单计算。
学习重点、难点
重点：线段的和差的概念，这是相关作图和计算的依据。
难点 ：第6题涉及较多的线段和较复杂的数量关系。
二、预习领航
- 从宾馆A出发去景点B有A—C—B，A—D—B两条道路。你有哪些方法判别哪条路更近些？
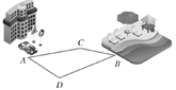
如果工具只有没有刻度的直尺和圆规，你有办法吗？
- 已知线段a=1.5cm，b=2.5cm，c=4cm。a、b、c三条线段的长度之间有怎样的关系？
（1）线段c的长度等于线段_____________的长度加上线段_____________的长度，那么线段c是线段_________加上线段_________，记做 ________ 。
（2）线段a的长度等于 ，那么线段a是 ，记做
如果一条线段的长度是另两条线段的长度的和，那么这条线段就叫做另两条线段的和； 如果一条线段的长度是另两条线段的长度的差，那么这条线段就叫做另两条线段的差； 两条线段的和或差仍是一条线段。 |
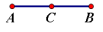
如图，C是线段AB上的一点.请完成下面的填空.
（1） AC＋CB＝________ .
（2） AB－CB＝________ .
（3） BC＝________ －AC.
如图,点Ｃ把线段ＡＢ分成相等的两条线段ＡＣ与ＢＣ， 点Ｃ叫做线段ＡＢ的中点。
则 AC＝ ＝ ，
BC＝ ＝ ，
AB＝ ＝ ．
三、新知导学
已知线段a，b（如图）。用直尺和圆规，求作：（1） a＋b； （2）b－a.
如图，Ｐ是线段ＡＢ的中点，点Ｃ，Ｄ把线段ＡＢ三等分．已知线段ＣＰ的长为2cm，求线段ＡＢ的长．
（二）课内练习
- 已知线段a，b（如图）.用直尺和圆规求作：（1）a－b；（2）2b.
- 已知线段AB，用刻度尺作出它的中点。
已知线段ＡＢ的长为ａ，延长线段ＡＢ至点Ｃ，使ＢＣ＝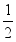
ＡＢ.问线段ＡＣ的长为多少？
四、课后检测
A 组题
- 如图，已知C是线段AB的中点，点D是线段AC的中点.请完成下列填空.
- 已知线段a，b（如图），用直尺和圆规求作：（1）2a；（2）2a－b.
- 已知线段ａ，利用刻度尺把线段ａ二等分．
- 已知线段ＡＢ＝ａ（如图），延长ＢＡ至点Ｃ，使ＡＣ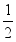＝ＡＢ．Ｄ为线段ＢＣ的中点．（1） 求ＣＤ的长． （2） 若ＡＤ＝3cm，求ａ的值．
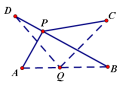
- 如图，Ａ，Ｂ，Ｃ，Ｄ表示四个村庄，村民们准备合打一口水井．
（1） 水井的位置现有Ｐ，Ｑ两种选择方案： 点Ｐ在线段ＢＤ上，点Ｑ在线段ＡＢ上. 哪一种方案的水井到各村庄的距离总和较小？
（2） 你能给出一种使水井到各村庄的距离之和最小的方案吗？ 若能，请标出水井的位置，并说明理由．
- 已知Ｐ为线段ＡＢ上一点，ＡＰ与ＰＢ的长度之比为2∶3．若ＡＰ＝4cm，求ＰＢ，ＡＢ的长．
B组题
- 如果我们没有带合适的测量工具，那么用我们身体的“尺子”来测量不失为好方法. 然而每个人“1拇”，“1肘”，“1拃”的长度不尽相同，所以测量者可先测量出自己的“1拇”，“1肘”和“1拃”究竟有多长.
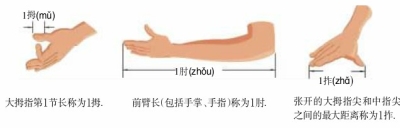
（1）你的“1拇”= ，“1肘”= ，“1拃”= ；
（2) 选择你身体中合适的“尺子”，测量数学课本的长为 ，宽为 ；
（3）用刻度尺量一量，数学课本的长为 ，宽为 。
（4）评价上述测量的精确程度.
五、教学反思
