沪教版（五四学制）初中数学 八年级上册 第17章《一元二次方程》复习课教案（表格式）

这是一份沪教版（五四学制）初中数学 八年级上册 第17章《一元二次方程》复习课教案（表格式），共4页。
                                        _ 月_ _日 星期__ 第__周课  题十七章一元二次方程课 型复习教 时1教  学目  标1.理解二次根式、最简二次根式、同类二次根式、分母有理化等概念的意义。2.掌握二次根式的性质，并能运用二次根式性质进行二次根式的运算。重  点二次根式有关性质的灵活应用，二次根式的正确运算。难  点二次根式有关性质的灵活应用，二次根式的正确运算。教具准备多媒体课件教   学   过   程教师活动学生活动一、建立知识结构：今天主要复习一元二次方程，请问在本章中你已经学习了哪些知识？教师帮助建立知识结构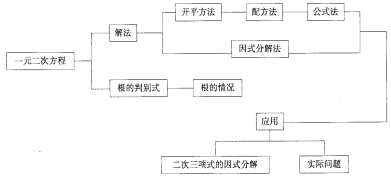： 学生回答，师生共同完成框架结构图： 二、例题解析1、概念辩析例1：判断下列各式哪些是一元二次方程？（口答）(1)；(2)；(3)；  (4)； (5)；(6). 适时小结：1、判断一元二次方程，要紧紧抓住“只含有一个未知数，未知数的最高次数是2，整式方程”这三个条件，缺一不可；2、确定一元二次方程各项及各项系数，先将方程化成一般形式．2、解法训练问题：对于例1中的方程1、4、6、8，如何来求解呢？ 例2：解下列方程.1、；2、 ；3、；4、． 适时小结：1、在解一元二次方程过程中运用降次策略转化成一元一次方程；2、公式法和配方法是通用的方法，有些特殊的一元二次方程，采用开平方法或因式分解法比较简便，应灵活选择适当的方法；3、方程中有括号，可整体考虑后再选取合适的方法.  3、根的判别式运用不解方程，判别下列关于的方程根的情况．（1）；（2）；（3）； 问：第（2）小题可以改成什么问题？ 解：，又，，即，无论取什么数值，方程总有两个不相等的实数根． 反馈练习：求证为任何实数时，关于的方程一定没有实数根．我们已经掌握了不解方程，判断一元二次方程根的情况．反之，如果知道根的情况，能否求出字母系数的取值范围呢？ 例3  如果关于的方程有实数根，试求的取值范围．解：关于x的一元二次方程有实数根，，即，变式1：如果关于的方程有两个实数根，试求的取值范围．问：与例3有什么不同？ 变式2：如果关于的方程有实数根，试求的取值范围．4、一元二次方程的应用我们学习了一元二次方程相关知识，请大家思考：若二次三项式在实数范围内能分解因式，则的取值范围是什么？ *例4在实数范围内分解因式：.师问：如何思考： 解：令=0.方程的两个实数根是，．∴= 2反馈练习    在实数范围内分解因式：.适时小结：二次三项式在实数范围内分解因式时应注意的问题：（1）二次项系数不要遗漏；（2）当含有x、y两个字母时，结果不能漏掉字母y；（3）要有把xy看做一个整体的思想.例题5 有一面积150平方米的长方形养鸡场，养鸡场的一边靠墙（墙长18米），墙对面设一个2米宽的门，另三边（门除外）用竹篱笆围成，篱笆总长33米，求养鸡场的长和宽各是多少米？ 例题6  某电扇厂4月份生产电风扇2000台，如果以后每月产量递增，且增长率相同，第二季度总共生产了9500台，求后两个月平均增长率.  三、畅谈收获请同学谈谈自己收获与感想. 四、回家作业：单元练习.  思考、回顾、复习旧知。                 学生口答                    学生在课堂练习上完成，请四位同学到黑板上板演过程，其他同学点评                  学生黑板板书，点评，纠错.              学生交流、讨论，分析不同处.                         把xy看做整体. 把=0看作关于xy的一元二次方程. 学生课堂练习本上完成，一学生板演，学生点评、纠错.                       谈收获和注意点 板书设计：              课后反思：