沪科版 初中数学 九年级上册 21.6 综合与实践　获取最大利润 教案

这是一份沪科版 初中数学 九年级上册 21.6 综合与实践　获取最大利润 教案，共5页。教案主要包含了题后反思等内容，欢迎下载使用。
第21章 二次函数与反比例函数
21.6　综合与实践　获取最大利润
教学目标
1.进一步理解二次函数最值的意义；
2.经历“问题情境一建立模型一求解验证”的过程,利用二次函数解决实际问题,感受函数模型思想和数学的应用价值；
3.能利用二次函数解决最大利润问题,进一步提高分析问题和解决问题的能力,增强数学的应用意识和创新意识.
教学重难点
重点：从实际问题中建立二次函数模型.
难点：设计如何获取最大利润问题的方案.
教学过程
复习巩固
利用二次函数解决实际问题中的最值的一般步骤：
(1)先求出函数表达式和自变量的取值范围；
(2)利用公式求最大值或最小值.
探究新知
【尝试】
例1　某商场销售一种进价为20元/台的台灯，经调查发现，该台灯每天的销售量w (台)与销售单价x(元)满足w＝-2x+80，设销售这种台灯每天的利润为y(元).
(1)求y关于x的函数表达式.
(2)当销售单价定为多少元时，每天的利润最大？最大利润是多少？
(3)在保证销售量尽可能大的前提下，该商场每天要想获得150元的利润，应将销售单价定为多少元？
【思考】(1)等量关系：每天的利润＝每台的利润×每天销售量；
(2)利用(1)中得到的函数的性质求最值；
(3)把y＝150代入(1)中的函数表达式，求得x的值.
解： (1)y＝(x-20)(-2x+80)＝-2x2+120x -1 600.
(2)∵ y＝-2x2+120x-1600＝-2(x-30)2+200，
∴ 当x＝30时，最大利润y＝200.
(3)令y＝150，得-2(x-30)2+200＝150，
解得x1＝25，x2＝35.
又销售量w＝-2x+80随单价x的增大而减小，故当x＝25时，既能保证销售量大，又可以每天获得150元的利润.
【思考】(小组讨论，老师引导)求解最大利润问题时要注意什么？
根据题意，舍去不合题意的x的值
例2　(小组讨论)
一个工厂在决定是否要生产某种产品时，往往向市场分析专家咨询该产品的市场情况.一种产品的销售量通常与销售单价有关，当单价上涨时，销售量下降.假设某市场分析专家提供了下列数据：
销售单价x/元
50
100
150
300
年销售量t/件
5 000
4 000
3 000
0
设生产t件该产品的成本为C＝50t+1 000.
回答下列问题：
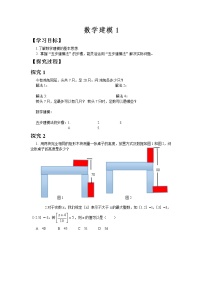
(1)画图并描出上述表格中各组数据对应的点.
(2)描出的这些点在一条直线上吗？求t和x之间的函数表达式.
(3)问当销售单价x和年销售量t各为多少时，年利润P最大？
【活动】(小组合作，老师指导)
（1） 如图所示.

（2） 这些点在一条直线上，t＝-20x+6 000(0