沪科版九年级上册21.1 二次函数精品第1课时教案

这是一份沪科版九年级上册21.1 二次函数精品第1课时教案，共5页。

第21章 二次函数与反比例函数

21.2　二次函数的图象和性质
21.2.1　二次函数y＝ax²的图象和性质
第1课时　二次函数y＝ax²(a>0)的图象和性质
教学目标
1.会用描点法画出二次函数y＝ax²(a＞0)的图象，能根据图象理解有关性质.
2.通过类比的方式由一次函数的探究方式得到研究特殊的二次函数图象及其性质的探究方式，并根据数形结合的思想探究函数之间的联系和区别.
3.通过画出函数图象，认识数形结合的思想方法，体会数学中的特殊与一般的辩证关系，体会数学的内在美.
教学重难点
重点：会画二次函数y＝ax²(a＞0)的图象.
难点：掌握二次函数y＝ax²(a＞0)的性质，并会灵活应用.
教学过程
复习巩固
(1)一次函数y＝kx+b(k≠0)的图象是__________.
特别地，正比例函数y＝kx(k≠0)的图象是________.
(2)描点法画一次函数的图象的步骤，分为_______，_______ ，______三个步骤.
(3)什么是二次函数？二次函数的一般形式是什么？
探究新知
【互动】1.你会用描点法画二次函数y＝x2的图象吗?
(1)列表：在y＝x2中自变量x可以是任意实数，列表表示几组对应值如下：
x
…
-3
-2
-1
0
1
2
3
…
y＝x2
…
9
4
1
0
1
4
9
…
(2)描点：根据表中x，y的数值在坐标平面中描点(x，y)；
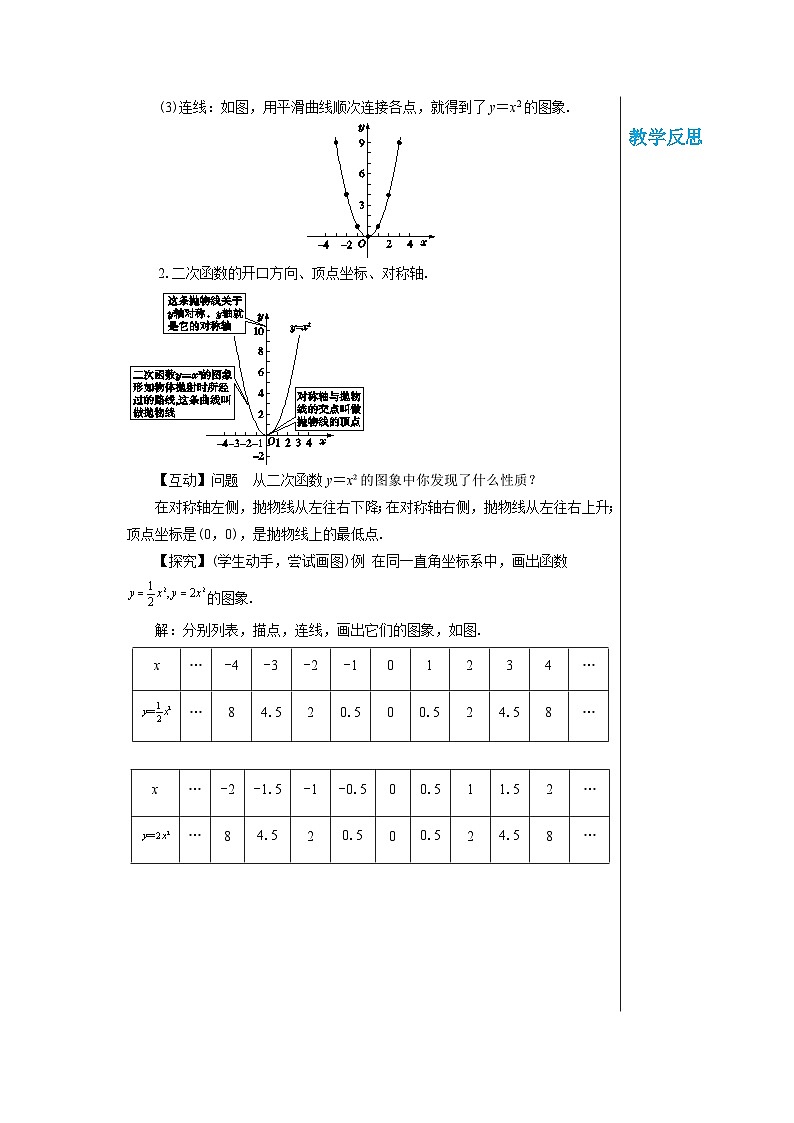
(3)连线：如图，用平滑曲线顺次连接各点，就得到了y＝x2的图象.

2.二次函数的开口方向、顶点坐标、对称轴.

【互动】问题 从二次函数y＝x²的图象中你发现了什么性质？
在对称轴左侧，抛物线从左往右下降；在对称轴右侧，抛物线从左往右上升；顶点坐标是(0，0)，是抛物线上的最低点.
【探究】(学生动手，尝试画图)例 在同一直角坐标系中，画出函数的图象.
解：分别列表，描点，连线，画出它们的图象，如图.
x
…
-4
-3
-2
-1
0
1
2
3
4
…

…
8
4.5
2
0.5
0
0.5
2
4.5
8
…

x
…
-2
-1.5
-1
-0.5
0
0.5
1
1.5
2
…

…
8
4.5
2
0.5
0
0.5
2
4.5
8
…

【探究】分别指出抛物线 的开口方向、对称轴和顶点坐标，再指出图象有最低点还是最高点？图象何时上升、下降？
【思考】观察图象，根据图象解答问题.
【互动】(小组归纳讨论，教师指导)总结y＝ax²(a＞0) 的图象和性质.






y＝ax2(a>0)
图象的形状
图象的特点
图象的性质

1
向x轴左右方向无限延伸
自变量x的取值范围是全体实数
2
是轴对称图形，对称轴是
y轴
对于x和-x可得到相同的函数值y
3
在y轴左侧是下降的；
在y轴右侧是上升的
当x<0时，函数值y随x的增大而减小；
当x>0时，函数值y随x的增大而增大.
4
顶点坐标是原点(0，0)，顶点是图象的最低点，开口向上，图象向上无限延伸
当x＝0时，y取得最小值，最小值为0，且y没有最大值，即y≥0

课堂练习
1.在平面直角坐标系中画出y＝3x²的图象，并完成以下问题：
(1)观察图象，说出图象的开口方向，顶点坐标，对称轴；
(2)说明在对称轴两侧部分，函数值y随x的变化而变化的情况.
2.已知二次函数y＝6x²，当x＞0时，y随x的增大而_________ .
3.若抛物线y＝(m-1)x²的开口向上，则m的取值范围是___________ .
4.已知二次函数y＝2x2， 若点(2，y1)与(3，y2)在此二次函数的图象上，则y1_____y2(填“>”“＝”或“<”).

参考答案
1.解：如图，(1)图象开口向上，顶点坐标(0,0)，对称轴是y轴；

(2)当x＜0时，函数值y随x的增大而减小；
当x＞0时，函数值y随x的增大而增大.
2.增大 3.m＞1 4.＜
课堂小结

布置作业

教材P27第1（1），2题.
板书设计


开口方向
对称轴
顶点坐标
最值
增减性
教学反思

































教学反思










































教学反思










































教学反思