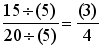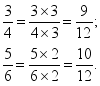沪教版 (五四制)六年级上册2.2 分数的基本性质一等奖表格教学设计
展开![]() 2.2分数的基本性质(1)
2.2分数的基本性质(1)
教学目标:
1.通过分数与除法的关系及除法的基本性质理解分数的基本性质.
2.通过动手实践的数学活动培养由具体到抽象的概括能力,渗透字母表示数的数学思想.
3.能运用分数的基本性质将一个分数化为分母不同而大小相等的分数.
教学重点与难点:
利用商不变性质迁移得到分数的基本性质.
教学过程:
教师活动 | 学生活动 | 设计意图 |
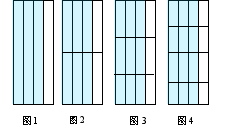
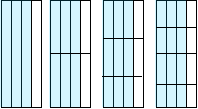
一、问题探究,发现规律 师:在上节课中我们知道两个正整数相除,它们的商可以用分数表示,即分数与除法有着密切的关系,今天这节课我们来继续研究分数. 下面请同学们思考:一张涂色的纸,涂色部分占这张纸的
问题1:在这些大小相同、不同等分的纸之中,涂色部分占整张纸的几分之几?这些分数有什么关系?
设问:为什么这些分数的大小是相等的? 师:折纸的方法虽不相同,也就是每张纸被平均分成了不同的等份,但由于每张纸的组涂色部分的大小是相同的,因而涂色部分占这张纸的几分之几也相等,即这些分数的大小是相等的.
师:通过折纸发现这四个分数的分子和分母都不相同,但分数的大小确是相同的,请同学们仔细观察这四个分数的分子和分母,看看有什么变化规律?
问题2:
问题3 : 请同学们分小组讨论
初步得到结论:如果将一个分数的分子分母同时都乘以或都除以同一个数,分数的大小不变. |
(1) (3)
预设学生可能回答:因为每组涂色部分的大小是相同的,所以这些分数的大小是相等的。 .教师纠正:因为每组涂色部分的大小是相同的,涂色部分占这张纸的几分之几也相等,所以这些分数的大小是相等的.
分子、分母同时乘以2、3、4可以得到
分子、分母同时除以4、3、2可以得到
| 新课开始时复习分数与除法的密切联系,为本节课利用商不变性质迁移得到分数的基本性质埋下伏笔.
通过思考,学生自己发现由于涂色部分的面积是相同,虽然对每个长方形进行了不同等分,但涂色部分占整张纸的几分之几是相等的,初步发现分数的基本性质.
|
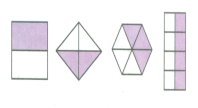
二、深入研究、概括规律 师:刚才我们对一个图形进行了不同等分,发现了如果将分数的分子分母同时都乘以或都除以同一个数,分数的大小不变,那么若对几个不同的图形进行等分,这种变化规律还存在吗? 思考: 1.分别将每一个图形中的涂色部分用分数表示,这些分数有什么关系?
2.在空白处填入适当的数: 小结:这些图形虽然大小、形状不一样,但涂色部分都占整个图形的一半,所以这些分数的大小都相等,刚才发现的分子和分母变化规律是仍然存在的. 大胆猜想: 分数的分子与分母同时乘以或同时除以同一个不为零的数,所得的分数与原分数大小相等.
师:数学是一门严密的学科,光猜想是不够的,我们是否可以运用我们所学过的知识来说明这个猜想是正确的呢? 1. 由分数与除法的关系可得
引导学生讨论:分子和分母同时乘或除以相同的数k、b时,k与b的取值是否有限定? 2.由除法运算中商不变的性质从而得到
归纳概括: 分数的基本性质:(板书) 分数的分子和分母都乘以或都除以同一个不为零的数,所得的分数与原分数的大小相等.即:
教师要点出性质中的关键词. |
虽然,图形大小、形状不一样,但每个图形中的涂色部分都是占整个图形的一半,这些分数的大小是相等的.
分数的分子、分母同时乘以4得:
预设学生回答时没有注意k与b的取值,教师补充提问引导学生深入思考.
|
通过大小、形状不同的图形中涂色部分与整体的关系,让学生进一步感悟分数的基本性质.
由分数与除法的关系,利用小学学过的除法运算中商不变的性质理解分数的基本性质,实现知识的迁移.
通过对k与b的取值的讨论,培养学生思维的严密性.
用符号语言表示分数的基本性质,即培养学生文字语言与数学语言之间的转化,又渗透字母表示数的数学思想. |
三、运用新知,解决问题 师:学习了分数的基本性质后,让我们一起来看看运用分数的基本性质可以帮助我们解决什么问题? 例1 试举出三个与分数 分析:要举出与分数 解:因为
同理: 所以 追问 这种分数还有吗?有多少个?
师:在例1中,运用分数基本性质可以将一个分数变为和它大小相等,分母不同的分数,这些分数的分母是没有指向性的,请看例2. 例2 把 师:此题中的分母是有指向性的,即都要化成15。我们该怎样将两个分数的分母由5、60变为15?依据是什么? 解:
适时小结: 运用分数的基本性质,既可将一个分数化成分母不同而大小相等的分数,也可把几个分母不同的分数化为分母相同的分数. |
预设回答:给分数同时乘以2、3等数. 教师纠正:运用分数的基本性质,将
有,有无数个.
根据分数的基本性质,将
将
|
正确运用分数基本性质,并能用分数的基本性质正确描述变化规律,以培养学生规范的数学语言表述能力.
通过追问,让学生理解运用分数基本性质可以将一个分数变为和它大小相等,分母不同的分数.
此题中继续让学生正确运用分数的基本性质描述变化规律,培养语言的规范性。通过问题的解决为后阶段学习通分奠定了基础.
|
四、课堂练习,巩固新知 A组 1.在括号内填上适当的数,使等式成立: (1) (2) (3) (4) 2.在括号内填上适当的数(课本:P.34/5) (1) (2) (3) (4)
| 1.(1) (2) (3) (4)
2.(1)24; (2)25;
(3)2; (4)36. 引导学生先观察每一题中已知的分子或分母之间发生了怎样的变化,再利用分数的基本性质对未知的分子或分母进行相同的变化.
|
通过观察发现分子分母同乘以哪一个数, 用分数的基本性质正确描述变化规律.
正确运用分数的基本性质发现变化规律,培养学生数学语言的规范表达. 以上A组8道题教师可通过统计正确率了解学生对分数的基本性质的掌握情况. |
B组 1.试写出三个与下列分数分母不同,并且与原分数大小相等的分数. (1) (3)
2.把 3.在一条数轴上分别用点表示分数
| 1.(1) (2) (3) 和每一个分数分母不同, 值相等的分数可以写出无数个. 2. 先把数轴上0—1的线段平均分成两份,取其中的一份,即为
| 正确运用分数基本性质,并理解运用分数基本性质可以将一个分数变为和它大小相等,分母不同的分数.
继续正确运用分数的基本性质把分母不同的分数化为分母相同的分数,为后续学习打下基础.
通过数形结合,体会在数轴上一个点可以表示不同的分数.这几个分数的大小相等. |
C组 *举出与 |
一共有5个. 方法1:把分子分母同时除以12和30的最大公因数6,化为 方法2:把分子分母同时除以12和30的公因数2、3、6,得到 提醒:分母30和25之间的关系不容易发现,学生可能会遗漏 | 进一步巩固分数的基本性质的应用,并为下节课约分做好预习工作. |
五、自主小结 1.分数的基本性质与分数除法的密切关系; 2.运用分数的基本性质时注意什么? 3.运用分数的基本性质可达到什么目的? 4.本节课所涉及的数学思想——字母代表数.
| 1.两个正整数相除,它们的商可以用分数表示,由除法运算中商不变的性质从而得到分数的基本性质. 2.运用分数的基本性质时注意一定要将分数的分子和分母同时都乘以或都除以一个数,并且这个数不能是零。 3.运用分数的基本性质,将分数的分子和分母同时都乘以或都除以一个不为零的数,可将一个分数化成分母不同而大小相等的分数. 4.本节课所涉及的数学思想——字母代表数. | 通过小结,回顾本节课所学新知,感受知识发生的过程及所涉及到的数学思想. |
课后作业:
试 题 | 解 答 | 设计意图 |
A组
(1) (2) (3)
(1) (2) (3) (4)
|
1. (1) 12(8÷2=4,从而3×4=12) (2) 6 (15÷5=3,从而2×3=6)
(3) 5 (15÷3=5,从而25÷5=5) (4) 3 (16÷2=8,从而24÷8=3)
2. (1)
(2)
(3) =;
(4) =.
3. |
正确运用分数的基本性质发现变化规律,准确填空.
判断分数的基本性质运用是否正确要抓住关键词“都”和“同一个不为零的数”.
继续正确运用分数的基本性质把分母不同的分数化为分母相同的分数. |
B组
(1) (2) (3)
*2. 判断下列说法是否正确: (1)分数的分子分母都乘以同一个数,分数的大小不变; ( ) (2) 分数的分子分母都加上或减去同一个数,分数的大小不变; ( ) (3)一个分数的分子扩大为原来的2倍,分母缩小为原来的一半,那么分数的值大小不变 ; ( )
|
1.(1)
方法1:可以在原来的分子和分母上同时依次乘以2、3、4等等,得出结论 方法2:把分子分母同时除以分子和分母的最大公因数得到一个分数,在这个分数的基础上把分子和分母上同时依次乘以2、3、4等等,得出结论. 这样的分数有无数个. 2. (1) (提醒学生分数的分子和分母都乘以或都除以同一个不为零的数,所得的分数与原分数的大小相等) (2) (分数的基本性质里没有分数的分子分母都加上或减去同一个数,分数的大小不变这条结论) (3) (可以通过举例说明;如分数 |
正确运用分数基本性质,并理解运用分数基本性质可以将一个分数变为和它大小相等,分母不同的分数.
这些判断题都不符合分数的基本性质,利用这几题加强对分数基本性质的理解,增强学生运用数学性质解决问题的能力. |
C组 *1.在一条数轴上分别用点表示分数
*2.写出在 | 1.先把数轴上0—1的线段平均分成两份,取其中的一份,即为 2.利用分数的基本性质,先把 |
巩固用数轴上的点表示分数的方法. 进一步巩固分数的基本性质的应用. |
初中数学沪教版 (五四制)六年级上册第二章 分数第1节 分数的意义和性质2.2 分数的基本性质公开课表格教案: 这是一份初中数学沪教版 (五四制)六年级上册第二章 分数第1节 分数的意义和性质2.2 分数的基本性质公开课表格教案,共8页。教案主要包含了复习引入,学习新知,练习巩固,自主小结等内容,欢迎下载使用。
沪教版 (五四制)六年级上册2.2 分数的基本性质一等奖表格教学设计: 这是一份沪教版 (五四制)六年级上册2.2 分数的基本性质一等奖表格教学设计,共8页。教案主要包含了复习引入,学习新知,运用新知,课堂练习,巩固新知,自主小结等内容,欢迎下载使用。
初中数学沪教版 (五四制)六年级上册2.2 分数的基本性质公开课表格教案: 这是一份初中数学沪教版 (五四制)六年级上册2.2 分数的基本性质公开课表格教案,共10页。教案主要包含了问题探究,发现规律,深入研究,运用新知,解决问题,课堂练习,巩固新知,自主小结等内容,欢迎下载使用。