




专题24.5 圆(压轴题综合测试卷)-2022-2023学年九年级数学上册从重点到压轴(人教版)(解析+原卷)
展开
这是一份专题24.5 圆(压轴题综合测试卷)-2022-2023学年九年级数学上册从重点到压轴(人教版)(解析+原卷),文件包含九年级数学上册专题245圆压轴题综合测试卷人教版原卷版docx、九年级数学上册专题245圆压轴题综合测试卷人教版解析版docx等2份试卷配套教学资源,其中试卷共52页, 欢迎下载使用。
 专题24.5 圆(满分100)学校:___________姓名:___________班级:___________考号:___________题号一二三总分得分 评卷人 得 分 一.选择题(本大题共10小题,每小题3分,满分30分)1.(2022·重庆忠县·九年级期中)如图,点B,C,D在⊙O上,若∠BCD=130°,则∠BOD的度数是( )
专题24.5 圆(满分100)学校:___________姓名:___________班级:___________考号:___________题号一二三总分得分 评卷人 得 分 一.选择题(本大题共10小题,每小题3分,满分30分)1.(2022·重庆忠县·九年级期中)如图,点B,C,D在⊙O上,若∠BCD=130°,则∠BOD的度数是( )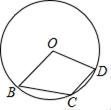 A.50° B.60° C.80° D.100°
A.50° B.60° C.80° D.100°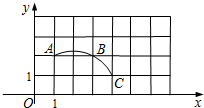 2.(2022·江苏·九年级专题练习)如图,在平面直角坐标系中,过格点A,B,C作一圆弧,点B与下列格点的连线中,能够与该圆弧相切的是( )A.点(0,3) B.点(2,3) C.点(5,1) D.点(6,1) 3.(2022·全国·九年级课时练习)如图,在
2.(2022·江苏·九年级专题练习)如图,在平面直角坐标系中,过格点A,B,C作一圆弧,点B与下列格点的连线中,能够与该圆弧相切的是( )A.点(0,3) B.点(2,3) C.点(5,1) D.点(6,1) 3.(2022·全国·九年级课时练习)如图,在![]() 中,点
中,点![]() 在弦
在弦![]() 上移动,连接
上移动,连接![]() 过点
过点![]() 作
作![]() 交
交![]() 于点
于点![]() .若
.若![]() 则
则![]() 的最大值是( )
的最大值是( )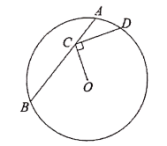 A.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 4.(2022·浙江丽水·模拟预测)已知⊙O的直径CD=10cm,AB是⊙O的弦,AB=8cm,且AB⊥CD,垂足为M,则AC的长为( )A.2
4.(2022·浙江丽水·模拟预测)已知⊙O的直径CD=10cm,AB是⊙O的弦,AB=8cm,且AB⊥CD,垂足为M,则AC的长为( )A.2![]() cm B.4
cm B.4![]() cm C.2
cm C.2![]() cm或4
cm或4![]() cm D.2
cm D.2![]() cm或4
cm或4![]() cm5.(2022·江苏·九年级)如图,
cm5.(2022·江苏·九年级)如图,![]() 是⊙
是⊙![]() 的直径,点C为圆上一点,
的直径,点C为圆上一点,![]() 的平分线交
的平分线交![]() 于点D,
于点D,![]() ,则⊙
,则⊙![]() 的直径为( )
的直径为( )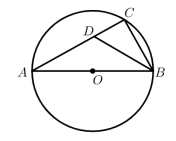 A.
A.![]() B.
B.![]() C.1 D.26.(2022·全国·九年级课时练习)如图,在
C.1 D.26.(2022·全国·九年级课时练习)如图,在![]() 中,
中,![]() ,以该三角形的三条边为边向形外作正方形,正方形的顶点
,以该三角形的三条边为边向形外作正方形,正方形的顶点![]() 都在同一个圆上.记该圆面积为
都在同一个圆上.记该圆面积为![]() ,
,![]() 面积为
面积为![]() ,则
,则![]() 的值是( )
的值是( )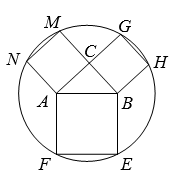 A.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 7.(2022·全国·九年级专题练习)如图,等边
7.(2022·全国·九年级专题练习)如图,等边![]() 中,
中,![]() ,点D,点E分别是边BC,CA上的动点,且
,点D,点E分别是边BC,CA上的动点,且![]() ,连接AD、BE交于点F,当点D从点B运动到点C时,则点F的运动路径的长度为( )
,连接AD、BE交于点F,当点D从点B运动到点C时,则点F的运动路径的长度为( ) A.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 8.(2022·全国·九年级课时练习)如图,在⊙O中,点C在优弧
8.(2022·全国·九年级课时练习)如图,在⊙O中,点C在优弧![]() 上,将弧
上,将弧![]() 沿BC折叠后刚好经过AB的中点D.若⊙O的半径为
沿BC折叠后刚好经过AB的中点D.若⊙O的半径为![]() ,AB=4,则BC的长是( )
,AB=4,则BC的长是( )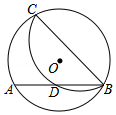 A.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 9.(2022·全国·九年级课时练习)如图,△ABC的内切圆⊙O与AB,BC,AC相切于点D,E,F,已知AB=6,AC=5,BC=7,则DE的长是( )
9.(2022·全国·九年级课时练习)如图,△ABC的内切圆⊙O与AB,BC,AC相切于点D,E,F,已知AB=6,AC=5,BC=7,则DE的长是( )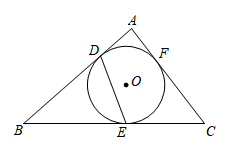 A.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 10.(2022·江苏无锡·九年级期中)我们定义:两边平方和等于第三边平方的2倍的三角形叫做奇异三角形,根据定义:①等边三角形一定是奇异三角形;②在Rt△ABC中,∠C=90°,AB=c,AC=b,BC=a,且b>a,若Rt△ABC是奇异三角形,则a:b:c=1:
10.(2022·江苏无锡·九年级期中)我们定义:两边平方和等于第三边平方的2倍的三角形叫做奇异三角形,根据定义:①等边三角形一定是奇异三角形;②在Rt△ABC中,∠C=90°,AB=c,AC=b,BC=a,且b>a,若Rt△ABC是奇异三角形,则a:b:c=1:![]() :2;③如图,AB是⊙O的直径,C是⊙O上一点(不与点A、B重合),D是半圆
:2;③如图,AB是⊙O的直径,C是⊙O上一点(不与点A、B重合),D是半圆![]() 的中点,C、D在直径AB的两侧,若在⊙O内存在点E,使AE=AD,CB=CE.则△ACE是奇异三角形;④在③的条件下,当△ACE是直角三角形时,∠AOC=120°,其中,说法正确的有( )
的中点,C、D在直径AB的两侧,若在⊙O内存在点E,使AE=AD,CB=CE.则△ACE是奇异三角形;④在③的条件下,当△ACE是直角三角形时,∠AOC=120°,其中,说法正确的有( )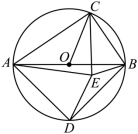 A.①② B.①③ C.②④ D.③④ 评卷人 得 分 二.填空题(本大题共5小题,每小题3分,满分15分)11.(2022·全国·九年级课时练习)工程上常用钢珠来测量零件上小圆孔的宽口,假设钢珠的直径是10mm,测得钢珠顶端离零件表面的距离为8mm,如图所示,则这个小圆孔的宽口AB的长度为____mm.
A.①② B.①③ C.②④ D.③④ 评卷人 得 分 二.填空题(本大题共5小题,每小题3分,满分15分)11.(2022·全国·九年级课时练习)工程上常用钢珠来测量零件上小圆孔的宽口,假设钢珠的直径是10mm,测得钢珠顶端离零件表面的距离为8mm,如图所示,则这个小圆孔的宽口AB的长度为____mm.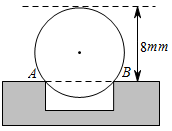 12.(2022·全国·九年级课时练习)已知⊙O的直径为10cm,AB,CD是⊙O的两条弦,
12.(2022·全国·九年级课时练习)已知⊙O的直径为10cm,AB,CD是⊙O的两条弦,![]() ,
,![]() ,
,![]() ,则
,则![]() 与
与![]() 之间的距离为________cm. 13.(2022·山东菏泽·九年级期中)如图,正方形
之间的距离为________cm. 13.(2022·山东菏泽·九年级期中)如图,正方形![]() 内接于
内接于![]() ,
,![]() ,
,![]() 分别与
分别与![]() 相切于点
相切于点![]() 和点
和点![]() ,
,![]() 的延长线与
的延长线与![]() 的延长线交于点
的延长线交于点![]() .已知
.已知![]() ,则图中阴影部分的面积为___________.
,则图中阴影部分的面积为___________. 14.(2022·全国·九年级课时练习)如图,⊙O是等边△ABC的外接圆,已知D是⊙O上一动点,连接AD、CD,若圆的半径r=2,则以A、B、C、D为顶点的四边形的最大面积为_____.
14.(2022·全国·九年级课时练习)如图,⊙O是等边△ABC的外接圆,已知D是⊙O上一动点,连接AD、CD,若圆的半径r=2,则以A、B、C、D为顶点的四边形的最大面积为_____. 15.(2022·全国·九年级课时练习)如图,在矩形ABCD中,
15.(2022·全国·九年级课时练习)如图,在矩形ABCD中,![]() ,
,![]() ,
,![]() 为AD上一点,且
为AD上一点,且![]() ,
,![]() 为BC边上的动点,以为EF直径作
为BC边上的动点,以为EF直径作![]() ,当
,当![]() 与矩形的边相切时,BF的长为______.
与矩形的边相切时,BF的长为______.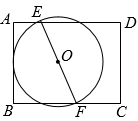 评卷人 得 分 三.解答题(本大题共9小题,满分55分)16.(6分)(2022·全国·九年级课时练习)在《阿基米德全集》中的《引理集》中记录了古希腊数学家阿基米德提出的有关圆的一个引理.如图,已知
评卷人 得 分 三.解答题(本大题共9小题,满分55分)16.(6分)(2022·全国·九年级课时练习)在《阿基米德全集》中的《引理集》中记录了古希腊数学家阿基米德提出的有关圆的一个引理.如图,已知![]() 是弦
是弦![]() 上一点,请你根据以下步骤完成这个引理的作图过程.
上一点,请你根据以下步骤完成这个引理的作图过程.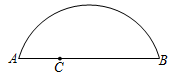 (1)尺规作图(保留作图痕迹,不写作法):①作线段
(1)尺规作图(保留作图痕迹,不写作法):①作线段![]() 的垂直平分线
的垂直平分线![]() ,分别交
,分别交![]() 于点
于点![]() 于点
于点![]() ,连接
,连接![]() ;②以点
;②以点![]() 为圆心,
为圆心,![]() 长为半径作弧,交
长为半径作弧,交![]() 于点
于点![]() (
(![]() 两点不重合),连接
两点不重合),连接![]() .(2)直接写出引理的结论:线段
.(2)直接写出引理的结论:线段![]() 的数量关系. 17.(6分)(2022·江西上饶·九年级期末)如图,⊙O的直径AB的长为2,点C在圆周上,∠CAB=30°.点D是圆上一动点,DE∥AB交CA的延长线于点E,连接CD,交AB于点F.(1)如图1,当DE与⊙O相切时,求∠CFB的度数;(2)如图2,当点F是CD的中点时,求△CDE的面积.
的数量关系. 17.(6分)(2022·江西上饶·九年级期末)如图,⊙O的直径AB的长为2,点C在圆周上,∠CAB=30°.点D是圆上一动点,DE∥AB交CA的延长线于点E,连接CD,交AB于点F.(1)如图1,当DE与⊙O相切时,求∠CFB的度数;(2)如图2,当点F是CD的中点时,求△CDE的面积.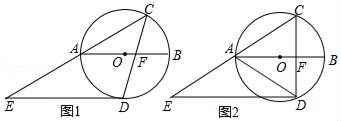 18.(6分)(2022·全国·九年级专题练习)如图,AB是半圆O的直径,点D是半圆O上一点,点C是
18.(6分)(2022·全国·九年级专题练习)如图,AB是半圆O的直径,点D是半圆O上一点,点C是![]() 的中点,CE⊥AB于点E,过点D的切线交EC的延长线于点G,连接AD,分别交CE、CB于点P、Q,连接AC.(1)求证:GP=GD;(2)求证:P是线段AQ的中点;(3)连接CD,若CD=2,BC=4,求⊙O的半径和CE的长.
的中点,CE⊥AB于点E,过点D的切线交EC的延长线于点G,连接AD,分别交CE、CB于点P、Q,连接AC.(1)求证:GP=GD;(2)求证:P是线段AQ的中点;(3)连接CD,若CD=2,BC=4,求⊙O的半径和CE的长.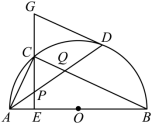 19.(6分)(2022·全国·九年级课时练习)对于平面直角坐标系xOy中的图形P,Q,给出如下定义:M为图形P上任意一点,N为图形Q上任意一点,如果M,N两点间的距离有最小值,那么称这个最小值为图形P,Q间的“非常距离”,记作
19.(6分)(2022·全国·九年级课时练习)对于平面直角坐标系xOy中的图形P,Q,给出如下定义:M为图形P上任意一点,N为图形Q上任意一点,如果M,N两点间的距离有最小值,那么称这个最小值为图形P,Q间的“非常距离”,记作![]() .已知点
.已知点![]() ,
,![]() ,连接AB.
,连接AB.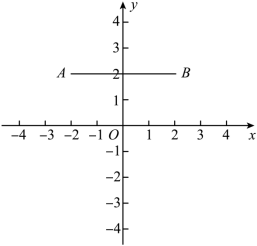 (1)d(点O,AB)= ;(2)⊙O半径为r,若
(1)d(点O,AB)= ;(2)⊙O半径为r,若![]() ,直接写出r的取值范围;(3)⊙O半径为r,若将点A绕点B逆时针旋转
,直接写出r的取值范围;(3)⊙O半径为r,若将点A绕点B逆时针旋转![]() ,得到点
,得到点![]() .①当
.①当![]() 时
时![]() ,求出此时r的值;②对于取定的r值,若存在两个α使
,求出此时r的值;②对于取定的r值,若存在两个α使![]() ,直接写出r的范围. 20.(6分)(2022·四川德阳·九年级阶段练习)如图1,四边形
,直接写出r的范围. 20.(6分)(2022·四川德阳·九年级阶段练习)如图1,四边形![]() 内接于
内接于![]() ,
,![]() 为直径,过点
为直径,过点![]() 作
作![]() 于点
于点![]() ,连接
,连接![]() .
.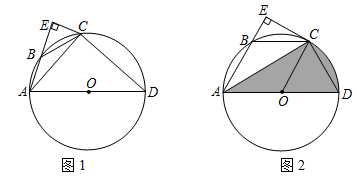 (1)求证:
(1)求证:![]() ;(2)若
;(2)若![]() 是
是![]() 的切线,
的切线,![]() ,连接
,连接![]() ,如图2.①请判断四边形ABCO的形状,并说明理由;②当AB=2时,求AD, AC与
,如图2.①请判断四边形ABCO的形状,并说明理由;②当AB=2时,求AD, AC与![]() 围成阴影部分的面积. 21.(6分)(2022·全国·九年级专题练习)如图,以AB为直径的
围成阴影部分的面积. 21.(6分)(2022·全国·九年级专题练习)如图,以AB为直径的![]() 上有一动点C,
上有一动点C,![]() 的切线CD交AB的延长线于点D,过点B作
的切线CD交AB的延长线于点D,过点B作![]() 交
交![]() 于点M,连接AM,OM,BC.
于点M,连接AM,OM,BC.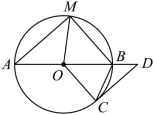 (1)求证:
(1)求证:![]() (2)若
(2)若![]() ,填空:①当AM= 时,四边形OCBM为菱形;②连接MD,过点O作
,填空:①当AM= 时,四边形OCBM为菱形;②连接MD,过点O作![]() 于点N,若
于点N,若![]() ,则ON= . 22.(6分)(2022·全国·九年级课时练习)如图,AB是⊙O的直径,P为AB上一点,弦CD与弦EF交于点P,PB平分∠DPF,连DF交AB于点G.
,则ON= . 22.(6分)(2022·全国·九年级课时练习)如图,AB是⊙O的直径,P为AB上一点,弦CD与弦EF交于点P,PB平分∠DPF,连DF交AB于点G.  (1)求证:CD=EF;(2)若∠DPF=60°,PE∶PF=1∶3,AB=2
(1)求证:CD=EF;(2)若∠DPF=60°,PE∶PF=1∶3,AB=2![]() ,求OG的长. 23.(6分)(2022·全国·九年级课时练习)问题提出:(1)如图1,已知
,求OG的长. 23.(6分)(2022·全国·九年级课时练习)问题提出:(1)如图1,已知![]() 是边长为2的等边三角形,则
是边长为2的等边三角形,则![]() 的面积为______.问题探究:(2)如图2,在
的面积为______.问题探究:(2)如图2,在![]() 中,已知
中,已知![]() ,
,![]() ,求
,求![]() 的最大面积.问题解决:(3)如图3,某校学生礼堂的平面示意图为矩形ABCD,其宽
的最大面积.问题解决:(3)如图3,某校学生礼堂的平面示意图为矩形ABCD,其宽![]() 米,长
米,长![]() 米,为了能够监控到礼堂内部情况,现需要在礼堂最尾端墙面CD上安装一台摄像头M进行观测,并且要求能观测到礼堂前端墙面AB区域,同时为了观测效果达到最佳,还需要从点M出发的观测角
米,为了能够监控到礼堂内部情况,现需要在礼堂最尾端墙面CD上安装一台摄像头M进行观测,并且要求能观测到礼堂前端墙面AB区域,同时为了观测效果达到最佳,还需要从点M出发的观测角![]() .请你通过所学的知识进行分析,在墙面CD区域上是否存在点M满足要求?若存在,求出MC的长度;若不存在,请说明理由.
.请你通过所学的知识进行分析,在墙面CD区域上是否存在点M满足要求?若存在,求出MC的长度;若不存在,请说明理由.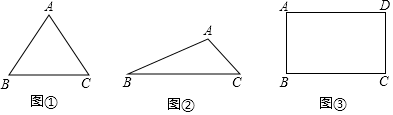 24.(7分)(2022·江苏·苏州中学九年级阶段练习)在Rt△ABC中,∠BCA=90°,CA=CB,点D是△ABC外一动点(点B,点D位于AC两侧),连接CD,AD.
24.(7分)(2022·江苏·苏州中学九年级阶段练习)在Rt△ABC中,∠BCA=90°,CA=CB,点D是△ABC外一动点(点B,点D位于AC两侧),连接CD,AD.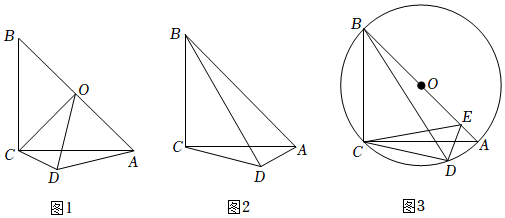 (1)如图1,点O是AB的中点,连接OC,OD,当△AOD为等边三角形时,∠ADC的度数是 ;(2)如图2,连接BD,当∠ADC=135°时,探究线段BD,CD,DA之间的数量关系,并说明理由;(3)如图3,⊙O是△ABC的外接圆,点D在
(1)如图1,点O是AB的中点,连接OC,OD,当△AOD为等边三角形时,∠ADC的度数是 ;(2)如图2,连接BD,当∠ADC=135°时,探究线段BD,CD,DA之间的数量关系,并说明理由;(3)如图3,⊙O是△ABC的外接圆,点D在![]() 上,点E为AB上一点,连接CE,DE,当AE=1,BE=7时,直接写出△CDE面积的最大值及此时线段BD的长.
上,点E为AB上一点,连接CE,DE,当AE=1,BE=7时,直接写出△CDE面积的最大值及此时线段BD的长.
相关试卷
这是一份初中数学人教版七年级上册1.2.1 有理数课后练习题,文件包含七年级数学上册专题18有理数压轴题综合训练卷人教版原卷版docx、七年级数学上册专题18有理数压轴题综合训练卷人教版解析版docx等2份试卷配套教学资源,其中试卷共33页, 欢迎下载使用。
这是一份专题23.1 旋转与几何综合(压轴题专项讲练)-2022-2023学年九年级数学上册从重点到压轴(人教版)(解析+原卷),文件包含九年级数学上册专题231旋转与几何综合压轴题专项讲练人教版原卷版docx、九年级数学上册专题231旋转与几何综合压轴题专项讲练人教版解析版docx等2份试卷配套教学资源,其中试卷共82页, 欢迎下载使用。
这是一份专题24.4 圆与四边形的综合(压轴题专项讲练)-2022-2023学年九年级数学上册从重点到压轴(人教版)(解析+原卷),文件包含九年级数学上册专题244圆与四边形的综合压轴题专项讲练人教版原卷版docx、九年级数学上册专题244圆与四边形的综合压轴题专项讲练人教版解析版docx等2份试卷配套教学资源,其中试卷共58页, 欢迎下载使用。










