22.1.2二次函数y=ax2的图像和性质(讲+练)【6种题型】-【重要笔记】2022-2023学年九年级数学上册重要考点精讲精练(人教版)(解析+原卷)
展开 22.1.2二次函数y=ax2的图像和性质
22.1.2二次函数y=ax2的图像和性质
![]()

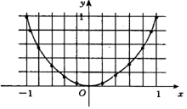
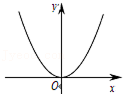
用描点法画出二次函数y=ax2(a≠0)的图象,如图,它是一条关于y轴对称的曲线,这样的曲线叫做抛物线. | |||||||||||||||||||||||||||||
二次函数y=ax2(a≠0)的图象的画法 用描点法画二次函数y=ax2(a≠0)的图象时,应在顶点的左、右两侧对称地选取自变量x的值,然后计算出对应的y值,这样的对应值选取越密集,描出的图象越准确. |
注意:用描点法画二次函数y=ax2(a≠0)的图象,该图象是轴对称图形,对称轴是y轴.画草图时应抓住以下几点:开口方向,对称轴,顶点,与 | ||||||||||||||||||||||||||||
题型1:利用描点法作函数图像
| |||||||||||||||||||||||||||||
【变式1-1】在如图所示的同一平面直角坐标系中,画出函数y=2x2,y=
| |||||||||||||||||||||||||||||
【变式1-2】画出下列函数的图象: (1)y=3x2; (2)y=﹣
| |||||||||||||||||||||||||||||
二次函数y=ax2(a≠0)的图象及性质 二次函数y=ax2(a≠0)的图象的性质,见下表:
| |||||||||||||||||||||||||||||
注意: | |||||||||||||||||||||||||||||
题型2:二次函数y=ax2的图像
A.
| |||||||||||||||||||||||||||||
【变式2-1】下列图象中,是二次函数y=x2的图象的是( ) A.
| |||||||||||||||||||||||||||||
【变式2-2】如图,在同一平面直角坐标系中,作出函数①y=3x2;②y=
A.①②③ B.①③② C.②③① D.③②① | |||||||||||||||||||||||||||||
题型3:二次函数y=ax2的性质
A.(0,0) B.(0,﹣3) C.(﹣3,0) D.(﹣3,﹣3) | |||||||||||||||||||||||||||||
【变式3-1】抛物线 A.0个 B.1个 C.2个 D.3个 | |||||||||||||||||||||||||||||
【变式3-2】.对于函数y=4x2,下列说法正确的是( ) A.当x>0时,y随x的增大而减小 B.当x>0时,y随x的增大而增大 C.y随x的增大而减小 D.y随x的增大而增大 | |||||||||||||||||||||||||||||
【变式3-3】二次函数y=﹣3x2的图象一定经过( ) A.第一、二象限 B.第三、四象限 C.第一、三象限 D.第二、四象限 | |||||||||||||||||||||||||||||
题型4:函数图像位置的识别
A.
| |||||||||||||||||||||||||||||
【变式4-1】函数y=ax2与y=ax+a,在第一象限内y随x的减小而减小,则它们在同一平面直角坐标系中的图象大致位置是( ) A.
| |||||||||||||||||||||||||||||
【变式4-2】在图中,函数y=﹣ax2与y=ax+b的图象可能是( ) A.
| |||||||||||||||||||||||||||||
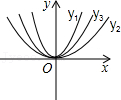
题型5:函数值的大小比较
A.y3<y1<y2 B.y3<y2<y1 C.y1<y2<y3 D.y2<y1<y3 | |||||||||||||||||||||||||||||
【变式5-1】函数y=﹣6x2,当x1>x2>0,则y1与y2的大小关系为y1 y2. | |||||||||||||||||||||||||||||
【变式5-2】函数y=x2的图象对称轴左侧上有两点A(a,15),B(b, | |||||||||||||||||||||||||||||
题型6:简单综合-三角形面积
| |||||||||||||||||||||||||||||
【变式6-1】已知函数y=ax2(a≠0)的图象与y=2x﹣3的图象交于点(1,b) (1)试求a和b的值; (2)求函数y=ax2的解析式,并求其图象的顶点坐标和对称轴; (3)x取何值时,二次函数y=ax2中的y随x值的增大而增大? (4)求抛物线与过点(0,﹣2)且与x轴平行的直线的两个交点与顶点构成的三角形的面积.
| |||||||||||||||||||||||||||||
【变式6-2】已知抛物线y=ax2(a≠0)与直线y=﹣2x+3交于点(﹣1,b). 求:(1)a,b的值; (2)抛物线与y=x+6的两交点及顶点所构成的三角形的面积.
| |||||||||||||||||||||||||||||
![]()
一、单选题
1.抛物线y=-2x2的对称轴是( )
A.直线x= ![]() B.直线x=-
B.直线x=- ![]() C.直线x=0 D.直线y=0
C.直线x=0 D.直线y=0
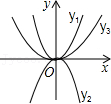
2.已知A(1,y1)、B(﹣2,y2)、C(﹣ ![]() ,y3)在函数y=x2的图象上,则y1、y2、y3的大小关系是( )
,y3)在函数y=x2的图象上,则y1、y2、y3的大小关系是( )
A.![]() <
< ![]() <
< ![]() B.
B.![]() <
< ![]() <
< ![]()
C.![]() <
< ![]() <
< ![]() D.
D.![]() <
< ![]() <
< ![]()
3.抛物线 ![]() 的顶点坐标是
的顶点坐标是 ![]()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.满足函数y= ![]() x﹣1与y=﹣
x﹣1与y=﹣ ![]() 的图象为( )
的图象为( )
A.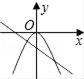 B.
B.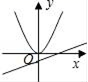
C.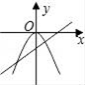 D.
D.
5.下列说法中错误的是( )
A.在函数y=-x2中,当x=0时y有最大值0
B.在函数y=2x2中,当x>0时y随x的增大而增大
C.抛物线y=2x2,y=-x2, ![]() 中,抛物线y=2x2的开口最小,抛物线y=-x2的开口最大
中,抛物线y=2x2的开口最小,抛物线y=-x2的开口最大
D.不论a是正数还是负数,抛物线y=ax2的顶点都是坐标原点
6.已知抛物线 ![]() 的开口向下,则
的开口向下,则 ![]() 的取值范围是( )
的取值范围是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.抛物线y= ![]() x2,y=4x2,y=-2x2的图像中,开口最大的是( )
x2,y=4x2,y=-2x2的图像中,开口最大的是( )
A.y= ![]() x2 B.y=4x2 C.y=-2x2 D.无法确定
x2 B.y=4x2 C.y=-2x2 D.无法确定
二、填空题
8.若在抛物线 ![]() 对称轴的左侧,y随x的增大而增大,则m= .
对称轴的左侧,y随x的增大而增大,则m= .
9.二次函数 ![]() 的图象开口方向是 (填“向上”或“向下”).
的图象开口方向是 (填“向上”或“向下”).
10.若抛物线 ![]() 开口向下,则
开口向下,则 ![]() .
.
11.已知二次函数 ![]() 的图象开口向下,则m的取值范围是 .
的图象开口向下,则m的取值范围是 .
12.已知二次函数y甲=mx2和y乙=nx2,对任意给定一个x值都有y甲≥y乙,关于m,n的关系正确的是 (填序号).①m<n<0 ②m>0,n<0 ③m<0,n>0 ④m>n>0
13.函数y=ax2(a≠0)与直线y=2x-3的图象交于点(1,b).
求:
(1)a和b的值;
(2)求抛物线y=ax2的开口方向、对称轴、顶点坐标;
(3)作y=ax2的草图.
14.在同一个直角坐标系中作出y= ![]() x2,y=
x2,y= ![]() x2-1的图象.
x2-1的图象.
(1)分别指出它们的开口方向、对称轴以及顶点坐标;
(2)抛物线y= ![]() x2-1与抛物线y=
x2-1与抛物线y= ![]() x2有什么关系?
x2有什么关系?
15.已知 ![]() 是二次函数,
是二次函数,
(1)若其图象开口向下,求k的值;
(2)若当 ![]() 时,y随x的增大而减小,求函数关系式.
时,y随x的增大而减小,求函数关系式.
初中数学人教版九年级下册26.1.1 反比例函数课时练习: 这是一份初中数学人教版九年级下册<a href="/sx/tb_c102625_t7/?tag_id=28" target="_blank">26.1.1 反比例函数课时练习</a>,文件包含2612反比例函数的图像和性质讲+练12大题型原卷版docx、2612反比例函数的图像和性质讲+练12大题型解析版docx等2份试卷配套教学资源,其中试卷共58页, 欢迎下载使用。
初中数学人教版九年级上册22.1.1 二次函数课后作业题: 这是一份初中数学人教版九年级上册22.1.1 二次函数课后作业题,文件包含九年级数学上册2211二次函数讲+练-重要笔记2022-2023学年九年级数学上册重要考点精讲精练人教版原卷版docx、九年级数学上册2211二次函数讲+练-重要笔记2022-2023学年九年级数学上册重要考点精讲精练人教版解析版docx等2份试卷配套教学资源,其中试卷共18页, 欢迎下载使用。
九年级上册25.1.2 概率同步训练题: 这是一份九年级上册25.1.2 概率同步训练题,文件包含九年级数学上册25概率7大题型-重要笔记2022-2023学年九年级数学上册重要考点精讲精练人教版原卷版docx、九年级数学上册25概率7大题型-重要笔记2022-2023学年九年级数学上册重要考点精讲精练人教版解析版docx等2份试卷配套教学资源,其中试卷共43页, 欢迎下载使用。