2022-2023学年湖北省荆州市江陵县八年级（下）期末数学试卷（含解析）

这是一份2022-2023学年湖北省荆州市江陵县八年级（下）期末数学试卷（含解析），共21页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

2022-2023学年湖北省荆州市江陵县八年级（下）期末数学试卷
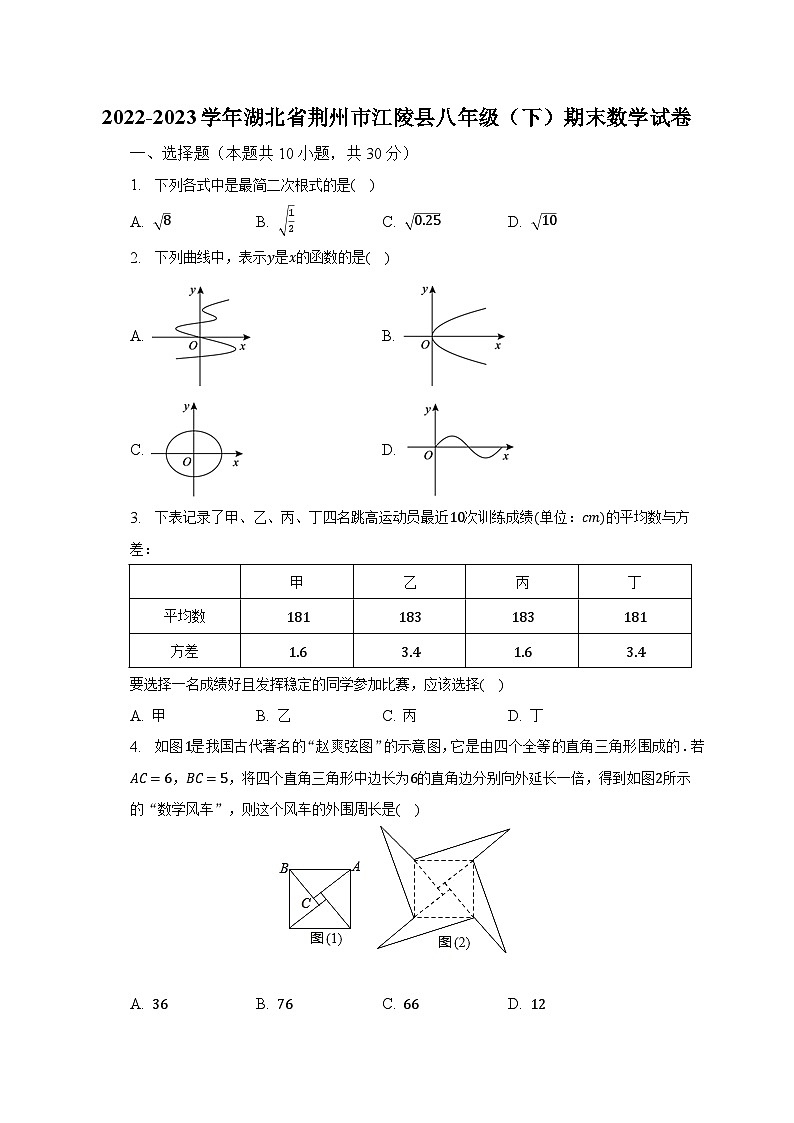
一、选择题（本题共10小题，共30分）
1. 下列各式中是最简二次根式的是(    )
A. 8 B. 12 C. 0.25 D. 10
2. 下列曲线中，表示y是x的函数的是(    )
A. B.
C. D.
3. 下表记录了甲、乙、丙、丁四名跳高运动员最近10次训练成绩(单位：cm)的平均数与方差：

甲
乙
丙
丁
平均数
181
183
183
181
方差
1.6
3.4
1.6
3.4
要选择一名成绩好且发挥稳定的同学参加比赛，应该选择(    )
A. 甲 B. 乙 C. 丙 D. 丁
4. 如图1是我国古代著名的“赵爽弦图”的示意图，它是由四个全等的直角三角形围成的．若AC=6，BC=5，将四个直角三角形中边长为6的直角边分别向外延长一倍，得到如图2所示的“数学风车”，则这个风车的外围周长是(    )

A. 36 B. 76 C. 66 D. 12
5. 如图，有一架秋千，当它静止时，踏板离地0.5米，将它往前推3米时，踏板离地1.5米，此时秋千的绳索是拉直的，则秋千的长度是(    )



A. 3米
B. 4米
C. 5米
D. 6米
6. 如图，在四边形ABCD中，E，F分别是AD，BC的中点，G，H分别是BD，AC的中点，AB=CD，∠ABD=20°，∠BDC=70°，则∠GEF的大小是(    )
A. 25°
B. 30°
C. 45°
D. 35°
7. 如图，在平面直角坐标系xOy中，菱形OABC的顶点C在x轴的正半轴上．若点A的坐标是(3,4)，则点B的坐标为(    )
A. (5,4)
B. (8,4)
C. (5,3)
D. (8,3)
8. 若 63n是整数，则正整数n的最小值是(    )
A. 3 B. 7 C. 9 D. 63
9. 点P(x,y)在第一象限内，且x+y=6，点A的坐标为(4,0).设△OPA的面积为S，则下列图象中，能正确反映面积S与x之间的函数关系式的图象是(    )
A. B.
C. D.
10. 在平面直角坐标系xOy中，对于点P(x,y)，我们把P1(y-1,-x-1)叫做点P的友好点.已知点A1的友好点为A2，点A2的友好点为A3，点A3的友好点为A4，这样依次得到各点.若A2023的坐标为(1,2)，则点A1的坐标为(    )
A. (1,2) B. (1,-2) C. (-3,-2) D. (-3,2)
二、填空题（本题共6小题，共24分）
11. 若 x-6在实数范围内有意义，则实数x的取值范围是          ．
12. 如图，分别以数轴的单位长度1和3为直角边的长作直角三角形，以数轴上的原点O为圆心，这个直角三角形的斜边长为半径作弧与数轴交于一点A，则点A表示的数为          ．





13. 如图，平行四边形ABCD的对角线AC与BD相交于点O，且∠OCD=90°.若E是BC边的中点，AC=6，BD=10，则OE的长为          ．






14. 如图，直线y=x+b与直线y=kx+6交于点P(3,5)，则关于x的不等式kx+6>x+b的解集是______．


15. 如图是由边长为1的小正方形组成的5×6网格，每个小正方形的顶点叫做格点，A，B，C都是格点，点E为线段AB边上一点.仅用无刻度的直尺在给定网格中完成画图，画图过程用虚线表示.在图中画▱ABCD，再在CD上画点F，使直线EF平分▱ABCD的周长．

16. 一次函数y=ax+b(a,b是常数，且a≠0)，若2a+b+3=0，则这个一次函数的图象必经的点是______ ．
三、解答题（本题共8小题，共66分）
17. (1)计算： 18+ 12-2 6× 34÷5 2；
(2)已知x=2+ 3，y=2- 3，求代数式x2-y2的值．
18. 《荆州市义务教育体育与健康考核评价方案》规定跳绳成为体育中考考试项目.某校体育组为了解八年级学生跳绳的基本情况，从八年级男、女生中各随机抽取了20名学生1分钟跳绳次数，并对数据进行整理、描述和分析.下面给出了部分信息．
a.学生1分钟跳绳次数频数分布直方图如图(数据分成9组：90≤x<100，100≤x<110，…，170≤x<180)：

b.男生1分钟跳绳次数在140≤x<150这一组的是：140，141，142，143，144，145，145，147
c.1分钟跳绳次数的平均数、中位数、优秀率如表：
组别
平均数
中位数
优秀率
男生
139
m
65%
女生
135
138
n
注：《国家中学生体质健康标准》规定：八年级男生1分钟跳绳次数大于或等于135个，成绩为优秀；八年级女生1分钟跳绳次数大于或等于130个，成绩为优秀.根据以上信息，回答下列问题：
(1)写出表中m，n的值；
(2)此次测试中，某学生的1分钟跳绳次数为140个，这名学生的成绩排名超过同组一半的学生，判断该生属于______ (填“男生”或“女生”)组；
(3)如果全年级男生人数为100人，女生人数为120人，请估计该年级跳绳成绩优秀的总人数．
19. 如图，在△ABC中，D是AB上一点，AD=DC，DE平分∠ADC交AC于点E，DF平分∠BDC交BC于点F，∠DFC=90°．
(1)求证：四边形CEDF是矩形；
(2)若∠B=30°，AD=2，连接BE，求BE的长．





20. 在平面直角坐标系xOy中，一次函数y=-2x+2图象与x轴、y轴分别相交于点A和点B．
(1)求A，B两点的坐标；
(2)点C在x轴上，若△ABC是以边AB为腰的等腰三角形，求点C的横坐标．
21. 阅读下面内容：我们已经学习了《二次根式》和《乘法公式》，聪明的你可以发现：当a>0，b>0时，∵( a- b)2=a-2 ab+b≥0，∴a+b≥2 ab，当且仅当a=b时取等号.请利用上述结论解决以下问题：
(1)当x>0时，x+1x的最小值为______ ；当x<0时，x+1x的最大值为______ ．
(2)当x>0时，求y=x2+3x+16x的最小值．
22. 某班“数学兴趣小组”根据学习一次函数的经验，对函数y=|x-2|的图象和性质进行了研究．探究过程如下，请补充完整．
(1)自变量x的取值范围是全体实数．如表是y与x的几组对应值：
x
…
-3
-2
-1
0
1
2
3
4
5
…
y
…
5
4
m
2
1
0
1
2
3
…
其中，m=______；
(2)如图，在平面直角坐标系xOy中，描出了以表中各对对应值为坐标的点，并画出了函数图象的一部分，请画出该函数图象的另一部分；
(3)观察函数图象发现，该函数图象的最低点坐标是______；当x<2时，y随x的增大而减小；当x≥2时，y随x的增大而______；
(4)进一步探究，
①不等式|x-2|≥1.5的解集是______；
②若关于x的方程|x-2|=kx(k≠0)只有一个解，则k的取值范围是______．

23. 为落实“精准联防联控，构筑群防群治严密防线”政策，某区现对A，B，C，D四个防疫物资存储站进行检查，发现A，B两个存储站的防疫物资仍有50吨和80吨的缺口，经防疫部门统筹调控，决定从C，D两个存储站进行调运.现已知C站有防疫物资100吨，D站有防疫物资30吨．
假设共有x吨物资将从A站运往C站：
(1)请你完成表格中其余吨数的填写：

A站
B站
C站
x
______
D站
______
______
(2)已知从C站调往A站的运费为350元/吨，从D站调往A站的运费为200元/吨，从C站调往B站的运费为450元/吨，从D站调往B站的运费为500元/吨，试求出总运费W(元)与x之间的函数关系式，并直接写出x的取值范围；
(3)在(2)的条件下，通过优化运输方式，C站到A站的运费每吨减少了m元，并经核算，总运费的最小值不低于46000元，试求m的取值范围．
24. 已知：直线y=-x+1与x轴、y轴分别交于A，B两点，点C为直线AB上一动点，连接OC，∠AOC为锐角，在OC上方以OC为边作正方形OCDE，连接BE，设BE=t．

(1)如图1，当点C在线段AB上时，判断BE与AB的位置关系，并说明理由；
(2)当C的横坐标为 32，求点E的坐标；
(3)直接写出点E的坐标(用含t的式子表示)．
答案和解析

1.【答案】D 
【解析】解：A、 8=2 2，故A不符合题意；
B、 12= 22，故B不符合题意；
C、 0.25= 14=12，故C不符合题意；
D、 10是最简二次根式，故D符合题意；
故选：D．
根据最简二次根式的定义，逐一判断即可解答．
本题考查了最简二次根式，熟练掌握最简二次根式的定义是解题的关键．

2.【答案】D 
【解析】解：A、不能表示y是x的函数，故此选项不合题意；
B、不能表示y是x的函数，故此选项不合题意；
C、不能表示y是x的函数，故此选项不合题意；
D、能表示y是x的函数，故此选项符合题意；
故选：D．
根据函数的定义解答即可．
此题主要考查了函数概念，关键是掌握在一个变化过程中有两个变量x与y，对于x的每一个确定的值，y都有唯一的值与其对应，那么就说y是x的函数，x是自变量．

3.【答案】C 
【解析】解：∵乙，丙的平均数较大，
∴从乙和丙中选择一人参加比赛，
∵S丙2 ∴选择丙参赛，
故选：C．
首先比较平均数，平均数相同时选择方差较小的运动员参加．
此题考查了平均数和方差，正确理解方差与平均数的意义是解题关键．

4.【答案】B 
【解析】解：依题意，设“数学风车”中的四个直角三角形的斜边长为x，则
x2=122+52=169，
所以x=13，
所以这个风车的外围周长是：(13+6)×4=76．
故选：B．
由题意∠ACB为直角，利用勾股定理求得外围中一条边，又由AC延伸一倍，从而求得风车的一个轮子，进一步求得四个．
此题考查了勾股定理的证明，本题是勾股定理在实际情况中的应用，并注意隐含的已知条件来解答此类题．

5.【答案】C 
【解析】解：设OA=OB=x米，
∵BC=DE=3米，DC=1.5米，
∴CA=DC-AD=1.5-0.5=1(米)，OC=OA-AC=(x-1)米，
在Rt△OCB中，OC=(x-1)米，OB=x米，BC=3米，
根据勾股定理得：x2=(x-1)2+32，
解得：x=5，
则秋千的长度是5米．
故选：C．
设OA=OB=x米，用x表示出OC的长，在直角三角形OCB中，利用勾股定理列出关于x的方程，求出方程的解即可得到结果．
此题考查了勾股定理的应用，熟练掌握勾股定理是解本题的关键．

6.【答案】A 
【解析】解：∵E，G分别是AD，BD的中点，
∴EG是△ADB的中位线，
∴EG=12AB，EG//AB，
∴∠EGD=∠ABD=20°，
同理可得：FG=12CD，FG//CD，
∴∠BGF=∠BDC=70°，
∴∠DGF=180°-∠BDC=110°，
∴∠EGF=∠EGD+∠FGD=130°，
∵AB=CD，
∴EG=FG，
∴∠GEF=12×(180°-130°)=25°，
故选：A．
根据三角形中位线定理得到EG=12AB，EG//AB，FG=12CD，FG//CD，根据平行线的性质求出∠EGD、∠DGF，进而求出∠EGF，再根据等腰三角形的性质、三角形内角和定理计算即可．
本题考查的是三角形中位线定理、等腰三角形的性质，掌握三角形的中位线平行于第三边，且等于第三边的一半是解题的关键．

7.【答案】B 
【解析】解：∵点A的坐标是(3,4)，
∴OA=5，
∵四边形OABC为菱形，
∴OA=AB=5，
则点B的坐标为(8,4)．
故选：B．
根据点A的坐标是(3,4)，可得OA的长，再根据菱形的四条边都相等即可得点B的坐标．
本题考查了菱形的性质、坐标与图形的性质，解决本题的关键是掌握菱形的性质．

8.【答案】B 
【解析】解：∵ 63n= 7×32n=3 7n，且 7n是整数；
∴3 7n是整数，即7n是完全平方数；
∴n的最小正整数值为7．
故选：B．
因为 63n是整数，且 63n= 7×32n=3 7n，则7n是完全平方数，满足条件的最小正整数n为7．
本题主要考查了二次根式的乘法法则，解题的关键是理解7n是完全平方数．

9.【答案】C 
【解析】解：∵点P(x,y)在第一象限内，且x+y=6，
∴y=6-x(0 ∵点A的坐标为(4,0)，
∴S=12×4×(6-x)=-2x+12(0 ∴C符合．
故选：C．
先用x表示出y，再利用三角形的面积公式即可得出结论．
本题考查的是一次函数的图象，在解答此题时要注意x，y的取值范围．

10.【答案】C 
【解析】解：根据题意，点A1的坐标为A1(x,y)，
则A2(y-1,-x-1)，A3(-x-2,-y)，A4(-y-1,x+1)，A5(x,y)，
由此可知，每四次一循环，
因为2023÷4=505⋯⋯3，
所以-x-2=1，-y=2，
解得：x=-3，y=-2，
所以A1(-3,-2)，
故选：C．
求出A2、A3、A4、A5的坐标，找到规律，即可求出A1的值．
本题考查了点的坐标的特征，解题关键是准确理解题意，发现变换规律，求出字母的值．

11.【答案】x≥6 
【解析】
【分析】
根据二次根式有意义的条件列不等式求解．
本题考查二次根式有意义的条件，理解二次根式有意义的条件(被开方数为非负数)是解题关键．
【解答】
解：由题意可得x-6≥0，
解得x≥6，
故答案为：x≥6．  
12.【答案】 10 
【解析】解：由题知，在直角三角形中，根据勾股定理得，
直角三角形的斜边= 12+32= 10，
则OA= 10，
∵点A是以原点O为圆心， 10为半径作弧与数轴的交点，
∴点A表示的数为 10．
故答案为： 10．
根据勾股定理求出直角三角形斜边的长度，也就求出了OA的长，结合图中点A的位置确定点A表示的数．
本题考查了实数与数轴，根据勾股定理确定斜边的长度，即确定OA的长度是解答本题的关键．

13.【答案】2 
【解析】解：∵四边形ABCD是平行四边形，BD=10，AC=6，
∴OC=3，OD=5，
∵∠OCD=90°，
∴CD= OD2-OC2= 52-32=4，
∵E是BC边的中点，O是BD的中点，
∴2OE=CD，
∴OE=2．
故答案为：2．
根据平行四边形的性质得出OC=3，OD=5，进而利用勾股定理得出CD的长，利用三角形中位线得出OE即可．
此题考查平行四边形的性质以及中位线定理，解题的关键是熟练运用平行四边形的性质．

14.【答案】x<3 
【解析】观察函数图象得到当x<3时，函数y=kx+6的图象都在y=x+b的图象上方，所以关于x的不等式kx+6>x+b的解集为x<3．
解：当x<3时，kx+6>x+b，
即不等式kx+6>x+b的解集为x<3．
故答案为：x<3．
本题考查了一次函数与一元一次不等式：从函数的角度看，就是寻求使一次函数y=ax+b的值大于(或小于)0的自变量x的取值范围；从函数图象的角度看，就是确定直线y=kx+b在x轴上(或下)方部分所有的点的横坐标所构成的集合．

15.【答案】解：如图，平行四边形ABCD，点F即为所求．
 
【解析】根据平行四边形的定义画出图形，连接AC，BD交于点O，作直线OE交CD于点F，点F即为所求．
本题考查作图-应用与设计作图，平行四边形的判定和性质，解题的关键是理解题意，灵活运用所学知识解决问题．

16.【答案】(2,-3) 
【解析】解：∵2a+b+3=0，
∴-3=2a+b．
∴在y=ax+b中，当x=2时，y=-3，
∴一次函数经过(2,-3)点，
故答案为：(2,-3)．
根据2a+b+3=0，可求-3=2a+b，根据一次函数与方程的关系可知当x=2时，y=-3，即可得到定点坐标．
本题主要考查一次函数与一元一次方程的关系，将已知等式和函数解析式进行对比是解决本题的关键．

17.【答案】解：(1) 18+ 12-2 6× 34÷5 2
=3 2+2 3-32 2÷5 2
=3 2+2 3-310；
(2)∵x=2+ 3，y=2- 3，
∴x+y=4,x-y=2 3，
∴x2-y2=(x+y)(x-y)=4×2 3=8 3． 
【解析】(1)先计算二次根式的乘除法运算，化简二次根式，再合并同类二次根式即可；
(2)先计算x+y=4,x-y=2 3，再把原式分解因式，整体代入求值即可．
本题考查的是二次根式的混合运算，因式分解的应用，熟记运算法则是解本题的关键．

18.【答案】女生 
【解析】解：(1)由男生1分钟跳绳次数频数分布直方图和140≤x<150这一组的数据可知，20名男生中，成绩从低到高排序，第10位和第11位的成绩分别是141，142，
因此男生组的中位数：m=141+1422=141.5；
女生1分钟跳绳次数大于或等于130个的人数为：5+6+1+1+1=14，
因此女生组的优秀率：n=1420×100%=70%，
故m=141.5，n=70%；
(2)这名学生的成绩140小于男生组的中位数141.5，大于女生组的中位数138，
因此该生属于女生，
故答案为：女生；
(3)由已知和(2)的结论知男生组的优秀率为65%，女生组的优秀率为70%，
100×65%+120×70%=65+84=149(人)，
因此估计该年级跳绳成绩优秀的总人数为149人．
(1)利用中位数的定义求m，利用八年级女生1分钟跳绳次数大于或等于130个的人数除以女生总人数求n；
(2)将这名学生的成绩与男生、女生成绩的中位数比较即可；
(3)利用样本估计总体的方法解决．
本题考查统计相关知识，掌握频数分布直方图、中位数的定义和应用，以及利用样本估计总体的方法是解题的关键．

19.【答案】(1)证明：∵DE平分∠ADC，DF平分∠BDC，
∴∠ADE=∠CDE=12∠ADC，∠CDF=12∠BDC，
∴∠CDE+∠CDF=12(∠ADC+∠BDC)=12×180°=90°，即∠EDF=90°，
∵AD=DC，
∴∠DCA=∠DAC，
∴∠CED=∠AED=12×180°=90°，
又∵∠DFC=90°，
∴四边形CEDF是矩形；
(2)解：由(1)可知，四边形CEDF是矩形，
∴∠CED=∠ECF=90°，
∴∠A=90°-∠B=90°-30°=60°，DE⊥AC，

∵AD=DC，
∴CE=AE，△ACD是等边三角形，
∴∠ACD=60°，AC=AD=2，
∴AE=CE=1，
∴DE= AD2-AE2= 22-12= 3，
∵∠DCB=∠ECF-∠ACD=90°-60°=30°，
∴∠DCB=∠B，
∴DB=DC=AD，
∴DE是△ABC的中位线，
∴BC=2DE=2 3，
在Rt△BCE中，由勾股定理得：BE= CE2+BC2= 12+(2 3)2= 13，
即BE的长为 13． 
【解析】(1)证∠EDF=90°，∠CED=90°，再由∠DFC=90°，即可得出结论；
(2)证△ACD是等边三角形，得∠ACD=60°，AC=AD=2，则AE=CE=1，再由勾股定理得DE= 3，然后由三角形中位线定理得BC=2DE=2 3，由勾股定理即可得出结论．
本题考查了矩形的判定与性质、等边三角形的判定与性质、三角形中位线定理以及勾股定理等知识，熟练掌握矩形的判定与性质是解题的关键．

20.【答案】解：(1)∵一次函数y=-2x+2图象与x轴、y轴分别相交于点A和点B，
∴令y=0，则-2x+2=0，解得x=1，
∴点A(1,0)，
令x=0，则y=2，
∴点B(0,2)．
(2)∵AO=1，BO=2，
∴AB= OA2+OB2= 12+22= 5，
∵△ABC是以边AB为腰的等腰三角形，
∴AB=AC= 5，
∴点C的横坐标为1+ 5或1- 5或-1． 
【解析】(1)利用坐标轴上点的坐标特征求出点A，点B坐标即可；
(2)由勾股定理可求AB的长，即可求解．
本题考查了一次函数图象上点的坐标特征，勾股定理等知识，解答此题的关键是熟知一次函数与坐标轴的交点坐标的求法．

21.【答案】2  -2 
【解析】解：(1)∵x>0，
∴x+1x≥2 x⋅1x=2；
∵x<0，
∴x+1x=-[-x+(-1x)]，
∵-x+(-1x)≥2，
∴x+1x≤-2，
故答案为：2，-2；
(2)∵x>0，
∴y=x2+3x+16x=x+3+16x≥2 x⋅16x+3=8+3=11，
∴y的最小值为11．
(1)根据题中的不等式求解；
(2)先把代数式变形，再利用题中的不等式求解．
本题考查了配方法的应用，理解题中的新方法是解题的关键．

22.【答案】3  (2,0)  增大  x≤0.5或x≥3.5  k<-1或k≥1 
【解析】解：(1)当x=-1时，y=|x-2|=3，
∴m=3，
故答案为：3；
(2)画出该函数图象的另一部分如图；

(3)观察函数图象发现，该函数图象的最低点坐标是(2,0)；当x<2时，y随x的增大而减小；当x≥2时，y随x的增大而增大；
故答案为：(2,0)，增大；
(4)观察图象，
①不等式|x-2|≥1.5的解集是x≤0.5或x≥3.5；
②若关于x的方程|x-2|=kx(k≠0)只有一个解，则k的取值范围是k<-1或k≥1；
故答案为：x≤0.5或x≥3.5；k<-1或k≥1．
(1)根据函数y=|x-2|，计算出当x=-1对应的函数值，从而可以求得m的值；
(2)根据(1)中表格的数据，可以画出相应的函数图象；
(3)根据函数图象即可求得；
(4)观察函数图象，可以得到满足题意的k的取值范围；
本题考查了一次函数与一元一次不等式、一次函数的图象和性质，解决本题的关键是根据图象回答问题．

23.【答案】(100-x)  (50-x)  (x-20) 
【解析】解：(1)由题知，从C站运往B站(100-x)吨，
D站运往A站(50-x)吨，
D站运往B站30-(50-x)=(x-20)吨．
故答案为：(100-x)，(50-x)，(x-20)．
(2)由题意有：W=350x+450(100-x)+200(50-x)+500(x-20)=200x+45000(20≤x≤50)，
(3)由题知：W=(350-m)x+450(100-x)+200(50-x)+500(x-20)=(200-m)x+45000，
当200-m>0时，
y关于x的函数是y随x的增大而增大，
∴x=20时w最小，此时：w=(200-m)×20+45000≥46000，
解得：0 当200-m<0时，
y关于x的函数是y随x的增大而减小，
∴当x=50时，w取最小值，此时w=(200-m)×50+45000≥46000，
解得：m≤180，与200-m<0矛盾，
∴0 (1)根据A，B两个存储站的防疫物资仍有50吨和80吨的缺口，经防疫部门统筹调控，决定从C，D两个存储站进行调运．现已知C站有防疫物资100吨，D站有防疫物资30吨，即可填表；
(2)根据从C站调往A站的运费为350元/吨，从D站调往A站的运费为200元/吨，从C站调往B站的运费为450元/吨，从D站调往B站的运费为500元/吨，即可得到W(元)与x之间的函数关系式；
(3)根据C站到A站的运费每吨减少了m元，其余路线运费不变，总运费的最小值不低于46000元，得到W、m、x之间的函数，再讨论即可．
本题考查一次函数的应用和一元一次不等式的应用，找准等量关系列出函数关系式时关键．

24.【答案】解：(1)直线y=-x+1与x轴，y轴分别交于A，B两点，
∴点A、B的坐标分别为(1,0)，(0,1)，
∴∠OBA=∠OAB=45°，
∵∠AOC+∠BOC=90°，∠BOE+∠BOC=90°，
∴∠AOC=∠BOE，
∵AO=BO，OC=OE，
∴△OAC≌△OBE(SAS)，
∴∠OAC=∠OBE=45°，AC=BE=t，
∴∠EBA=∠EBO+∠OBA=∠OAC+∠OBA=45°+45°=90°，
∴BE=AB；
(2)如图，过点E作EH⊥OB于点H，

∵∠EBH=45°，
∴在Rt△EHB中，
BH=EH= 22BE= 22t，
∵C的横坐标为 32，点C在直线y=-x+1上，
∴C的纵坐标为1- 32，
由(1)知△OAC≌△OBE(SAS)，
∴AC=BE=t= 2- 62，
∴EH=BH=1- 32，
∵B(0,1)，
∴OB=1，
∴OH=OB-BE=1-(1- 32)= 32，
故点E的坐标为(-1+ 32, 32)；
(3)当点C在线段AB上时，如图，过点E作EH⊥OB于点H，

∵∠EBH=45°，
∴BH=EH= 22BE= 22t，
故点E的坐标为(- 22t,1- 22t)；
当点C在线段BA的延长线上时，如图，

同理可得，点E的坐标为( 22t,1+ 22t)；
综上，点E的坐标为(- 22t,1- 22t)，( 22t,1+ 22t)． 
【解析】(1)证明△OAC≌△OBE(SAS)，则∠OAC=∠OBE=45°，进而求得；
(2)∠EBH=45°，则BH=EH= 22BE= 22t，即可求解；
(3)分两种情况：当点C在线段AB上时，当点C在线段BA的延长线上时，结合∠EBH=45°，写出E点坐标即可．
本题是一次函数的综合题，主要考查一次函数的性质、正方形的性质、三角形全等，解直角三角形等，确定△OAC≌△OBE是解题的关键．