21.1 一元二次方程

一、教学目标

（1）通过具体实例认识旋转，并探索它的基本性质.

（2）理解对应点到旋转中心的距离相等、对应点与旋转中心所连线段的夹角等于旋转角、旋转前后图形全等的性质.

（3）能够按要求作出简单平面图形旋转后的图形，体验旋转在现实生活中的应用.

二、教学重难点

（1）教学重点：旋转的概念、性质；

（2）教学难点：旋转作图；

知识点一：旋转的概念

把一个平面图形绕着平面内某一点O转动一个角度，叫做图形的旋转，点O叫做旋转中心，转动的角叫做旋转角.

【提醒】

(1)    旋转的范围是在平面内旋转，否则有可能旋转成立体图形，因此,“在平面内”这一条件不可忽略.
(2)图形的旋转是由旋转中心与旋转角决定的，要准确描述旋转，需指明旋转方向，如顺时针旋转或逆时针旋转，即图形旋转的主要因素是旋转中心、旋转角度和旋转方向，其旋转中心在旋转的过程中始终保持不动，图形上每个点的旋转方向是相同的.
(3)如果图形上的点P经过旋转变为点P’，那么这两个点叫做这个旋转的对应点；线段两端点的对应点所确定的线段是原线段的对应线段；两边旋转后的对应边所组成的角是原角的对应角.

例1.钟表的运动可以看作是一种旋转现象，那么分针匀速旋转时，它的旋转中心是钟表的旋转轴的轴心，经过45分钟旋转了　   　度．

例2.时钟的时针在不停地旋转，从下午3时到下午6时（同一天），时针旋转的角度是　   　．

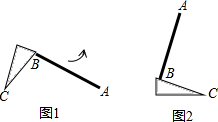
变式1.如图1，教室里有一只倒地的装垃圾的灰斗，BC与地面的夹角为50°，∠C=25°，小贤同学将它扶起平放在地面上（如图2），则灰斗柄AB绕点C转动的角度为　 　．

知识点二：旋转的性质

（1）对应点到旋转中心的距离相等；

（2）对应点与旋转中心所连线段的夹角等于旋转角；

（3）旋转前、后的图形全等.

【提醒】

运用旋转的性质时要找准对应关系，利用旋转的性质可得出相等的线段和相等的角，在线段或角的计算、证明线段相等或角相等时经常用到.

例1．如图，将△ABC绕点C顺时针旋转90°得到△EDC．若点A，D，E在同一条直线上，∠ACB=20°，则∠ADC的度数是（　　）

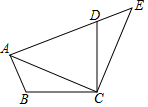
A．55° B．60° C．65° D．70°

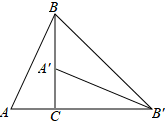
例2.如图，将Rt△ABC绕直角顶点C顺时针旋转90°，得到△A′B′C，连接BB'，若∠A′B′B=20°，则∠A的度数是　   　．

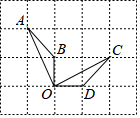
变式1.如图，点A、B、C、D、O都在方格纸的格点上，若△COD是由△AOB绕点O按顺时针方向旋转而得到的，则旋转的角度为　   　．

知识点三：旋转作图

旋转作图的步骤：

(1)明确题目要求：弄清旋转中心、旋转方向和旋转角.

(2)分析所作图形：找到已知图形的各关键点.

(3)作各关键点的对应点：将各关键点与旋转中心连接，以旋转中心为顶点，以已知点与旋转中心连线为

边，向旋转方向作一个角等于旋转角，使所作角的另一边的长等于已知边.

(4)作出新图形：按原图形顺次连接各对应点，即得到所求作的图形.

(5)写出结论：说明作出的图形.

【提醒】

根据旋转的性质可知，对应点与旋转中心所连线段的夹角等于旋转角，对应线段也相等，由此可以通过作相等的角，在角的边上截取相等的线段的方法，找到对应点，顺次连接对应点得出旋转后的图形.

例1.等边三角形至少旋转　   　度才能与自身重合．

例2.如图所示的图案，可以看成是由字母“Y”绕中心每次旋转　 　度构成的．

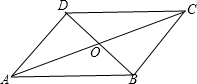
变式1.如图平行四边形ABCD是旋转对称图形，点　　是旋转中心，旋转了　　度后能与自身重合，则AD=　　，DC=　　，AO=　　，DO=　　．

拓展点一：图形旋转的识别

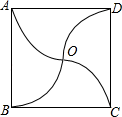
例1.如图，正方形ABCD边长为2cm，以各边中心为圆心，1cm为半径依次作圆，将正方形分成四部分．

（1）这个图形　　旋转对称图形（填“是”或“不是”）；若是，则旋转中心是点　　，最小旋转角是　　度．

（2）求图形OBC的周长和面积．

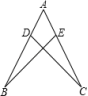
例2.如图，已知AD=AE，AB=AC．

（1）求证：∠B=∠C；

（2）若∠A=50°，问△ADC经过怎样的变换能与△AEB重合？

拓展点二：图案的观察分析问题

例1.在平面直角坐标系xOy中，将点N（﹣1，﹣2）绕点O旋转180°，得到的对应点的坐标是（　　）

A．（1，2） B．（﹣1，2） C．（﹣1，﹣2） D．（1，﹣2）

例2.如图，将线段AB绕点P按顺时针方向旋转90°，得到线段A'B'，其中点A、B的对应点分别是点A'、B'，则点A'的坐标是（　　）

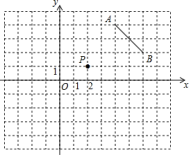
A．（﹣1，3） B．（4，0） C．（3，﹣3） D．（5，﹣1）

例3.如图，在平面直角坐标系中，把△ABC绕原点O旋转180°得到△CDA，点A，B，C的坐标分别为（﹣5，2），（﹣2，﹣2），（5，﹣2），则点D的坐标为（　　）

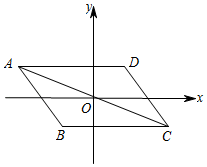
A．（2，2） B．（2，﹣2） C．（2，5） D．（﹣2，5）

拓展点三：旋转的性质的应用

例1．将矩形ABCD绕点A顺时针旋转α（0°＜α＜360°），得到矩形AEFG．

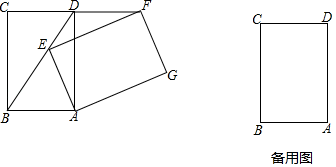
（1）如图，当点E在BD上时．求证：FD=CD；

（2）当α为何值时，GC=GB？画出图形，并说明理由．

例2.如图所示，将△AOB绕着点O旋转180度得到△DOC，过点O的一条直线分别交BA、CD的延长线于点E、F，求证：AE=DF．

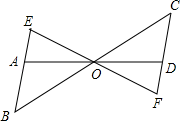
拓展点四：坐标系中图形的旋转问题

例1.在平面直角坐标系中，以原点为旋转中心，把点A（3，4）逆时针旋转90°，得到点B，则点B的坐标为（　　）

A．（4，﹣3） B．（﹣4，3） C．（﹣3，4） D．（﹣3，﹣4）

例2.正方形ABCD在坐标系中的位置如图所示，将正方形ABCD绕D点顺时针旋转90°后，B点的坐标为（　　）

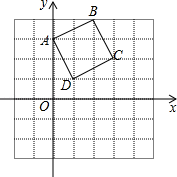
A．（﹣2，2） B．（4，1） C．（3，1） D．（4，0）

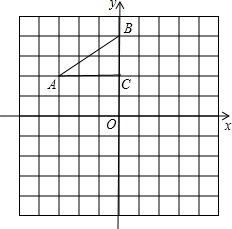
变式1.如图，在平面直角坐标系中，Rt△ABC的三个顶点分别是A（﹣3，2），B（0，4），C（0，2）．

（1）将△ABC以点C为旋转中心旋转180°，画出旋转后对应的△A1B1C1，平移△ABC，应点A2的坐标为（0，﹣4），画出平移后对应的△A2B2C2；

（2）若将△A1B1C1绕某一点旋转可以得到△A2B2C2，请直接写出旋转中心的坐标．

拓展点五：利用旋转性质解题

例1.如图，在菱形ABCD中，∠BAD=α，点E在对角线BD上．将线段CE绕点C顺时针旋转α，得到CF，连接DF．

（1）求证：BE=DF；

（2）连接AC，若EB=EC，求证：AC⊥CF．

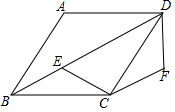
例2.如图，已知△ABC中，AB=AC，把△ABC绕A点顺时针方向旋转得到△ADE，连接BD，CE交于点F．

（1）求证：△AEC≌△ADB；

（2）若AB=，∠BAC=45°，当四边形ADFC是菱形时，求BF的长．