


27.4正多边形和圆同步练习-华东师大版数学九年级下册
展开
这是一份27.4正多边形和圆同步练习-华东师大版数学九年级下册,共7页。
![]() 27.4正多边形和圆同步练习-华东师大版数学九年级下册学校:___________姓名:___________班级:___________考号:___________ 一、单选题1.下列命题是假命题的是( )A.半径为R的圆内接正方形的边长等于
27.4正多边形和圆同步练习-华东师大版数学九年级下册学校:___________姓名:___________班级:___________考号:___________ 一、单选题1.下列命题是假命题的是( )A.半径为R的圆内接正方形的边长等于![]() B.正六边形的每个中心角都等于60°C.正八边形是轴对称图形D.正七边形是中心对称图形2.如图,
B.正六边形的每个中心角都等于60°C.正八边形是轴对称图形D.正七边形是中心对称图形2.如图,![]() 是正六边形ABCDEF的外接圆,P为
是正六边形ABCDEF的外接圆,P为![]() 上除C,D外的任意一点,则
上除C,D外的任意一点,则![]() 的值为( )
的值为( )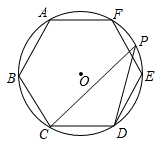 A.
A.![]() B.1 C.
B.1 C.![]() D.
D.![]() 3.如图,四边形
3.如图,四边形![]() 内接于
内接于![]() ,延长
,延长![]() 至点
至点![]() ,连接
,连接![]() .若四边形
.若四边形![]() 是菱形,
是菱形,![]() ,则
,则![]() 的度数为是( )
的度数为是( )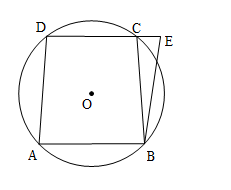 A.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 4.如图,A、B、C、D为一个正多边形的顶点,O为正多边形的中心,若
4.如图,A、B、C、D为一个正多边形的顶点,O为正多边形的中心,若![]() ,则这个正多边形的边数为( )
,则这个正多边形的边数为( )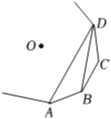 A.8 B.9 C.10 D.115.如图,A,B是⊙O上的两点,C是⊙O上不与A,B重合的任意一点. 如果∠AOB=140°,那么∠ACB的度数为( )
A.8 B.9 C.10 D.115.如图,A,B是⊙O上的两点,C是⊙O上不与A,B重合的任意一点. 如果∠AOB=140°,那么∠ACB的度数为( )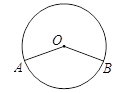 A.70° B.110° C.140° D.70°或110°6.如图,正五边形
A.70° B.110° C.140° D.70°或110°6.如图,正五边形![]() 内接于
内接于![]() ,点F是
,点F是![]() 上的动点,则
上的动点,则![]() 的度数为( )
的度数为( )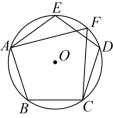 A.60° B.72° C.144° D.随着点
A.60° B.72° C.144° D.随着点![]() 的变化而变化7.在矩形ABCD中,AB=6,BC=4,有一个半径为1的硬币与边AB、AD相切,硬币从如图所示的位置开始,在矩形内沿着边AB、BC、CD、DA滚动到开始的位置为止,硬币自身滚动的圈数大约是
的变化而变化7.在矩形ABCD中,AB=6,BC=4,有一个半径为1的硬币与边AB、AD相切,硬币从如图所示的位置开始,在矩形内沿着边AB、BC、CD、DA滚动到开始的位置为止,硬币自身滚动的圈数大约是 A.1圈 B.2圈 C.3圈 D.4圈8.由四个图1所示的四边形和四个图2所示的菱形拼成一个正八边形(如图3),则图3中阴影部分面积与空白部分面积之比为( )
A.1圈 B.2圈 C.3圈 D.4圈8.由四个图1所示的四边形和四个图2所示的菱形拼成一个正八边形(如图3),则图3中阴影部分面积与空白部分面积之比为( )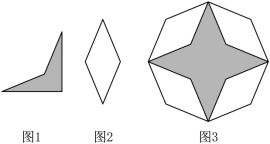 A.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 9.如图,面积为
9.如图,面积为![]() 的正方形
的正方形![]() 内接于⊙O,则
内接于⊙O,则![]() 的长度为( )
的长度为( ) A.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 10.如图,正六边形ABCDEF内接于⊙O,连接BD.则∠CBD的度数是( )
10.如图,正六边形ABCDEF内接于⊙O,连接BD.则∠CBD的度数是( )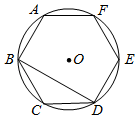 A.30° B.45° C.60° D.90° 二、填空题11.如图,
A.30° B.45° C.60° D.90° 二、填空题11.如图,![]() 中,
中,![]() 是边E上的高,
是边E上的高,![]() 分别是
分别是![]() 的内切圆,则
的内切圆,则![]() 与
与![]() 的面积比为 .
的面积比为 .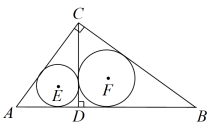 12.正六边形的边长为2,则其外接圆的半径为 ,正六边形的面积为 .13.半径为1的圆的内接正三角形的边长为 .14.如图,多边形ABCDE是⊙O的内接正五边形,则∠ACD等于 °.
12.正六边形的边长为2,则其外接圆的半径为 ,正六边形的面积为 .13.半径为1的圆的内接正三角形的边长为 .14.如图,多边形ABCDE是⊙O的内接正五边形,则∠ACD等于 °. 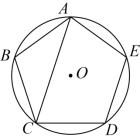 15.刘徽是我国魏晋时期卓越的数学家,他首次提出“割圆术”,利用圆内接正多边形逐步逼近圆来近似计算圆周率,方法如图:作正六边形ABCDEF内接于
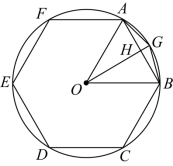
15.刘徽是我国魏晋时期卓越的数学家,他首次提出“割圆术”,利用圆内接正多边形逐步逼近圆来近似计算圆周率,方法如图:作正六边形ABCDEF内接于![]() ,取
,取![]() 的中点G,
的中点G,![]() 与
与![]() 交于点H;连接
交于点H;连接![]() 、
、![]() ;依次对剩余五段弧取中点可得一个圆内接正十二边形,记正十二边形的面积为
;依次对剩余五段弧取中点可得一个圆内接正十二边形,记正十二边形的面积为![]() ,正六边形的面积为
,正六边形的面积为![]() ,则
,则![]() .
. 16.如图,已知PA、PB是⊙O的两条切线,点A、点B为切点,线段OP交⊙O于点M.下列结论:①PA=PB;②OP⊥AB;③四边形OAPB有外接圆;④点M是△AOP外接圆的圆心.其中正确的结论是 (填序号).
16.如图,已知PA、PB是⊙O的两条切线,点A、点B为切点,线段OP交⊙O于点M.下列结论:①PA=PB;②OP⊥AB;③四边形OAPB有外接圆;④点M是△AOP外接圆的圆心.其中正确的结论是 (填序号).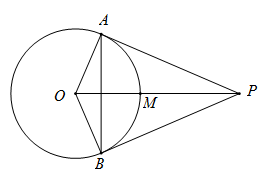 17.如图,AD是正五边形ABCDE的一条对角线,则∠BAD= °.
17.如图,AD是正五边形ABCDE的一条对角线,则∠BAD= °.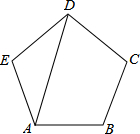 18.如图,正六边形
18.如图,正六边形![]() 内接于
内接于![]() ,正六边形的周长是
,正六边形的周长是![]() ,则
,则![]() 的半径是 .
的半径是 .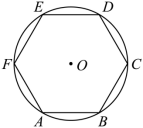 19.若正六边形的周长为6,则它的面积为 .20.如图,A、B、C、P是⊙O上的四个点,∠ACB=60°,且PC平分∠APB,则△ABC的形状是 .
19.若正六边形的周长为6,则它的面积为 .20.如图,A、B、C、P是⊙O上的四个点,∠ACB=60°,且PC平分∠APB,则△ABC的形状是 .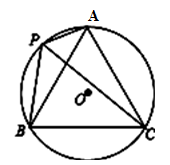
参考答案:1.D2.D3.A4.C5.D6.B7.B8.B9.C10.A11.![]() 12. 2 6
12. 2 6![]() 13.
13.![]() 14.7215.
14.7215.![]() 16.①②③17.72.18.
16.①②③17.72.18.![]() 19.
19.![]() 20.等边三角形
20.等边三角形





