27.2.1点与圆的位置关系同步练习-华东师大版数学九年级下册

27.2.1点与圆的位置关系同步练习-华东师大版数学九年级下册

学校:___________姓名：___________班级：___________考号：___________

一、单选题

1．若⊙O的半径为5，点P到圆心的距离为d，当点P在圆上时，则有（  ）

A．d＜5 B．d＞5 C．d = 5 D．d =

2．已知⊙O的半径为3，OP＝5，则点P与⊙O的位置关系是（    ）

A．点P在⊙O内 B．点P在⊙O上 C．点P在⊙O外 D．不能确定

3．半径为5的，圆心在直角坐标系的原点，则点与的位置关系是（    ）

A．在上 B．在内 C．在外 D．不能确定

4．若⊙A的半径是5，圆心A的坐标是，点P的坐标是，则点P与⊙A的位置关系是（    ）

A．在⊙A内 B．在⊙A上 C．在⊙A外 D．不能确定

5．平面内有两点P、O，⊙O的半径为1，若，则点P与⊙O的位置关系是（    ）．

A．点P在⊙O外 B．点P在⊙O上 C．点P在⊙O内 D．无法判断

6．已知⊙O的半径为5，若点P在⊙O内，则OP的长可以是（　　）

A．4 B．5 C．6 D．7

7．已知圆O的半径为5，同一平面内有一点P，且，则点P与圆O的关系是（    ）

A．点P在圆内 B．点P在圆外 C．点P在圆上 D．无法确定

8．已知⊙O的直径为6，点A到圆心O的距离为d，且点A在⊙O的外部，则（　　）

A．d ≥6 B．d ≥3 C．d >6 D．d >3

9．已知⊙O的半径为6cm，P到圆心O的距离为7cm，则点P在⊙O（ ）

A．外部 B．内部 C．上 D．不能确定

10．已知△ABC中，AB＝BC，若以点B为圆心，以AB为半径作圆，则点C在（　　）

A．在⊙B上 B．在⊙B外 C．在⊙B内 D．不能确定

二、填空题

11．在中，，，，是中线，以为圆心，以长为半径画圆，则点与的位置关系是        ．

12．已知Rt△ABC中，∠C=90°，AC=3，BC=，CD⊥AB，垂足为点D，以点D为圆心作⊙D，使得点A在⊙D外，且点B在⊙D内．设⊙D的半径为r，那么r的取值范围是         ．

13．已知⊙O的半径为4cm，若OP=3cm，那么点P与⊙O的位置关系是：         ．

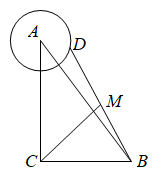
14．在中，，点D是以点A为圆心，半径为1的圆上一点，连接BD并取中点M，则线段CM的长最大为      ，最小为       ．

15．若圆O的半径是5，圆心的坐标是（0，0），点P的坐标是（－4，3），则点P与⊙O的位置关系是         ．

16．已知⊙O的半径为1，点P到圆心O的距离为d，若关于x的方程没有实根，则点P与⊙O的位置关系是    ．

17．如果⊙O的半径为r，点P到圆心O的距离为d，那么：①点P在⊙O外，则      ；②         则d=r；③      则d<r.

18．已知圆O的面积为，若点P在圆上，则      ．

19．已知直径为8，点到点O距离为5，则点在      ．（填“上、内或外”）

20．已知⊙O与点P在同一平面内，若⊙O的半径为6，线段OP的长为4，则点P与⊙O的位置关系是          ．

三、解答题

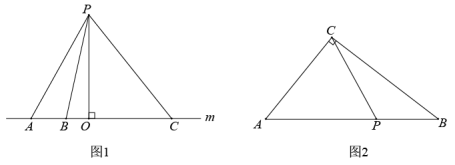
21．（1）回归教材：北师大七年级下册P44，如图1所示，点P是直线m外一点，，点O是垂足，点A、B、C在直线m上，比较线段PO，PA，PB，PC的长短，你发现了什么？

最短线段是______，于是，小明这样总结：直线外一点与直线上各点连接的所有线段中，______．

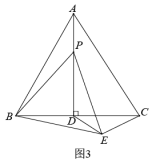
（2）小试牛刀：如图2所示，中，，，．则点P为AB边上一动点，则CP的最小值为______．

（3）尝试应用：如图3所示是边长为4的等边三角形，其中点P为高AD上的一个动点，连接BP，将BP绕点B顺时针旋转60°得到BE，连接PE、DE、CE．

①请直接写出DE的最小值．

②在①的条件下求的面积．

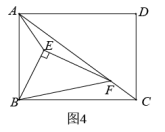
（4）拓展提高：如图4，顶点F在矩形ABCD的对角线AC上运动，连接AE．．，，请求出AE的最小值．

22．如图，在△ABC中，AB＝AC＝10cm，BD⊥AC于D，且BD＝8cm．点M从点A出发，沿AC方向匀速运动，速度为2cm/s；同时直线PQ由点B出发沿BA方向匀速运动，速度为1cm/s，运动过程中始终保持PQ∥AC，直线PQ交AB于P，交BC于Q，连接PM，设运动时间为t（s）（0＜t＜5）．

（1）当四边形PQCM是平行四边形时，求t的值；

（2）当t为何值时，△PQM是等腰三角形？

（3）以PM为直径作⊙E，在点P、Q整个运动过程中，是否存在这样的时刻t，使得⊙E与BC相切？若存在，请求出运动时间t的值；若不存在，请说明理由．

23．圆圆在解答问题“在矩形中，以A为圆心作，使得B，C，D三点中至少有一点在内，有一点在外，求的半径r的取值范围？”时，答案为“”．圆圆的答案对吗？如果错误，请写出正确的解答过程．

24．在平面直角坐标系xOy中，对于P、Q两点给出如下定义：若点P到x、y轴的距离中的最大值等于点Q到x、y轴的距离中的最大值，则称P、Q两点为“等距点”，如图1中的P、Q两点即为“等距点”．

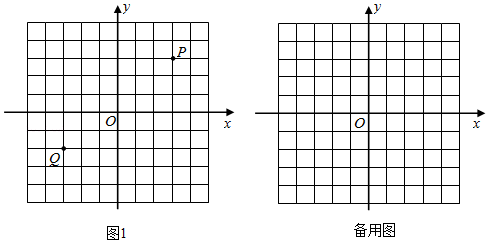
(1)已知点A的坐标为(-3,1)．

①在点E(0,3)、F(3,-3)、G(3,-5)中，点A的“等距点”是 　 　；

②若点B在直线y=x+4上，且A、B两点为“等距点”，则点B的坐标为 　 　；

(2)直线l：y=kx-2(k＞0)与x轴交于点C，与y轴交于点D．

①若T1(-1,t1)、T2(4,t2)是直线l上的两点，且T1、T2为“等距点”，求k的值；

②当k时，半径为r的⊙O上存在一点M，线段CD上存在一点N，使得M、N两点为“等距点”，直接写出r的取值范围．

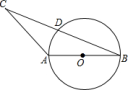
25．如图，在中，，是线段的中点，以为直径作，试判断点与的位置关系．

参考答案：

1．C

2．C

3．A

4．B

5．A

6．A

7．A

8．D

9．A

10．A

11．在上

12．．

13．点P在⊙O内

14．     3     2

15．点P在圆上

16．点在⊙O外

17．     d>r     点P在⊙O上     点P在⊙O内

18．5

19．外

20．点P在⊙O内

21．（1）PO，垂线段最短；（2）；（3）①DE的最小值是1；②△BPE的面积为；（4）AE的最小值为．

22．（1） t＝ （2）t＝（3）存在．当t＝或时，⊙E与BC相切

23．不正确，

24．(1)①E、F；②(-1，3)

(2)①；②r

25．点在上．