


华师大版九年级下册26.3 实践与探索当堂检测题
展开
这是一份华师大版九年级下册26.3 实践与探索当堂检测题,共10页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。
![]() 26.3实践与探索同步练习-华东师大版数学九年级下册学校:___________姓名:___________班级:___________考号:___________ 一、单选题1.抛物线y=ax2+bx+1的顶点为D,与x轴正半轴交于A、B两点,A在B左,与y轴正半轴交于点C,当△ABD和△OBC均为等腰直角三角形(O为坐标原点)时,b的值为( )
26.3实践与探索同步练习-华东师大版数学九年级下册学校:___________姓名:___________班级:___________考号:___________ 一、单选题1.抛物线y=ax2+bx+1的顶点为D,与x轴正半轴交于A、B两点,A在B左,与y轴正半轴交于点C,当△ABD和△OBC均为等腰直角三角形(O为坐标原点)时,b的值为( )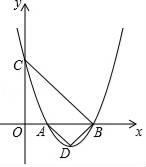 A.2 B.﹣2或﹣4 C.﹣2 D.﹣42.某种商品的成本是
A.2 B.﹣2或﹣4 C.﹣2 D.﹣42.某种商品的成本是![]() 元,试销阶段每件商品的售价
元,试销阶段每件商品的售价![]() (元)与产品的销售量
(元)与产品的销售量![]() (件)满足当
(件)满足当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,且
,且![]() 是
是![]() 的一次函数,为了获得最大利润
的一次函数,为了获得最大利润![]() (元),每件产品的销售价应定为( )A.160元 B.180元 C.140元 D.200元3.如图1,某地大桥主桥墩结构为抛物线形,桥墩的高度和宽度分别为40m和30m,若建立如图2所示的平面直角坐标系,则该抛物线的表达式为( )
(元),每件产品的销售价应定为( )A.160元 B.180元 C.140元 D.200元3.如图1,某地大桥主桥墩结构为抛物线形,桥墩的高度和宽度分别为40m和30m,若建立如图2所示的平面直角坐标系,则该抛物线的表达式为( )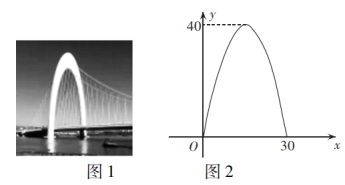 A.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 4.2022年9月29日国产大飞机C919从上海浦东机场第四跑道起飞,并于9时54分安全着陆,这标志着我国具备了按照国际通行适航标准研制大型客机的能力,如果某型号飞机降落后滑行的距离s(单位:米)关于滑行的时间t(单位:秒)的函数解析式是
4.2022年9月29日国产大飞机C919从上海浦东机场第四跑道起飞,并于9时54分安全着陆,这标志着我国具备了按照国际通行适航标准研制大型客机的能力,如果某型号飞机降落后滑行的距离s(单位:米)关于滑行的时间t(单位:秒)的函数解析式是![]() ,则该飞机着陆后滑行最长时间为( )A.243秒 B.486秒 C.18秒 D.36秒5.如下图,在直角坐标系的第一象限内,△AOB是边长为2的等边三角形,设直线l:x=t(0≤t≤2)截这个三角形所得位于直线左侧的图形(阴影部分)的面积为f(t),则函数s=f(t)的图象只可能是t大于等于0小于等于1时,函数为Y=3根号x方除以2 图线不应为直线( )
,则该飞机着陆后滑行最长时间为( )A.243秒 B.486秒 C.18秒 D.36秒5.如下图,在直角坐标系的第一象限内,△AOB是边长为2的等边三角形,设直线l:x=t(0≤t≤2)截这个三角形所得位于直线左侧的图形(阴影部分)的面积为f(t),则函数s=f(t)的图象只可能是t大于等于0小于等于1时,函数为Y=3根号x方除以2 图线不应为直线( )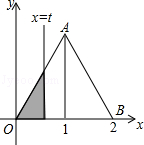 A.
A.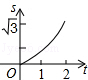 B.
B.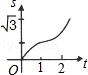 C.
C.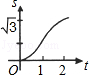 D.
D.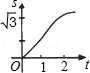 6.小明在周末外出的路上经过了如图所示的隧道,他想知道隧道顶端到地面的距离,于是他查阅了相关资料,知道了隧道的截面是由抛物线和矩形构成的.如图,以矩形的顶点A为坐标原点,地面AB所在直线为x轴,竖直方向为y轴,建立平面直角坐标系,抛物线的表达式为
6.小明在周末外出的路上经过了如图所示的隧道,他想知道隧道顶端到地面的距离,于是他查阅了相关资料,知道了隧道的截面是由抛物线和矩形构成的.如图,以矩形的顶点A为坐标原点,地面AB所在直线为x轴,竖直方向为y轴,建立平面直角坐标系,抛物线的表达式为![]() ,如果AB=8 m,AD=2 m,则隧道顶端点N到地面AB的距离为( )
,如果AB=8 m,AD=2 m,则隧道顶端点N到地面AB的距离为( )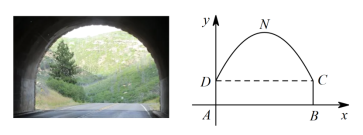 A.8 m B.7 m C.6 m D.5 m7.如图,在
A.8 m B.7 m C.6 m D.5 m7.如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,矩形
,矩形![]() 的顶点
的顶点![]() 在边
在边![]() 上,
上,![]() ,
,![]() 两点分别在边
两点分别在边![]() ,
,![]() 上,且
上,且![]() .将矩形
.将矩形![]() 以每秒1个单位长度的速度沿射线
以每秒1个单位长度的速度沿射线![]() 方向匀速运动,当点
方向匀速运动,当点![]() 与点
与点![]() 重合时停止运动,设运动时间为
重合时停止运动,设运动时间为![]() 秒,矩形
秒,矩形![]() 与
与![]() 重叠部分的面积为
重叠部分的面积为![]() ,则反映
,则反映![]() 与
与![]() 的函数关系的图象为( )
的函数关系的图象为( )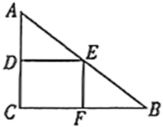 A.
A.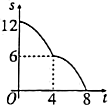 B.
B.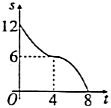 C.
C.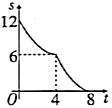 D.
D.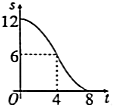 8.已知某汽车刹车后行驶的距离y(单位:m)与行驶的时间t(单位:s)之间近似满足函数关系y=-6t2+15t,根据上述函数模型和数据,可推断出该汽车刹车后到停下来所用的时间为( )A.1.25s B.2.25s C.0.25s D.0.759.某厂家2022年2月份生产口罩产量为180万只,4月份生产口罩的产量为461万只,设从2月份到4月份该厂家口罩产量的平均月增长率为x,根据题意可得方程( )A.
8.已知某汽车刹车后行驶的距离y(单位:m)与行驶的时间t(单位:s)之间近似满足函数关系y=-6t2+15t,根据上述函数模型和数据,可推断出该汽车刹车后到停下来所用的时间为( )A.1.25s B.2.25s C.0.25s D.0.759.某厂家2022年2月份生产口罩产量为180万只,4月份生产口罩的产量为461万只,设从2月份到4月份该厂家口罩产量的平均月增长率为x,根据题意可得方程( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 10.如图,正△ABC中,点P为BC边上的任意一点(不与点B,C重合),且∠APD= 60° ,PD交边AB于点D.设BP= x ,BD= y ,右图为y关于x的函数大致图象,下列判断中正确的是( )
10.如图,正△ABC中,点P为BC边上的任意一点(不与点B,C重合),且∠APD= 60° ,PD交边AB于点D.设BP= x ,BD= y ,右图为y关于x的函数大致图象,下列判断中正确的是( )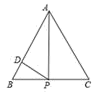
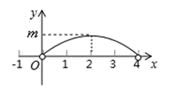 ①正△ABC中边长为4;②图象的函数表达式是
①正△ABC中边长为4;②图象的函数表达式是![]() , 其中 0<x<4;③ m=1A.①②③ B.①② C.②③ D.①③ 二、填空题11.如图是某地一座抛物线形拱桥,桥拱在竖直平面内,与水平桥面相交于
, 其中 0<x<4;③ m=1A.①②③ B.①② C.②③ D.①③ 二、填空题11.如图是某地一座抛物线形拱桥,桥拱在竖直平面内,与水平桥面相交于![]() 两点,拱桥最高点
两点,拱桥最高点![]() 到
到![]() 的距离为
的距离为![]() 为拱桥底部的两点,且
为拱桥底部的两点,且![]() 若
若![]() 的长为
的长为![]() 则点
则点![]() 到直线
到直线![]() 的距离为
的距离为 ![]()
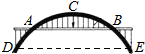 12.如图,在Rt△ABO中,∠AOB=90°,AO+BO=5,延长AO到C,使OC=3,延长BO到D,使OD=4,连接BC、CD、DA,则四边形ABCD面积的最大值为 .
12.如图,在Rt△ABO中,∠AOB=90°,AO+BO=5,延长AO到C,使OC=3,延长BO到D,使OD=4,连接BC、CD、DA,则四边形ABCD面积的最大值为 .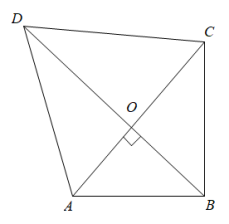 13.“十一”黄金周,某商场以每件30元的价格购进一种商品,试销中发现,这种商品每天的销售量m(件)与每件的销售价x(元),满足关系:m =140-x.写出商场卖这种商品每天的销售利润 y与每件的售价x之间的函数关系式是 .14.从地面竖直向上抛出一小球,小球的高度h(单位:米)与小球运动时间t(单位:秒)的函数关系式是h=9.8t﹣4.9t2.若小球的高度为4.9米,则小球的运动时间为 .15.如图,2016年里约奥运会上,某运动员在10米跳台跳水比赛时估测身体
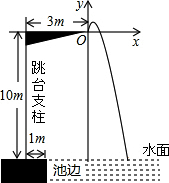
13.“十一”黄金周,某商场以每件30元的价格购进一种商品,试销中发现,这种商品每天的销售量m(件)与每件的销售价x(元),满足关系:m =140-x.写出商场卖这种商品每天的销售利润 y与每件的售价x之间的函数关系式是 .14.从地面竖直向上抛出一小球,小球的高度h(单位:米)与小球运动时间t(单位:秒)的函数关系式是h=9.8t﹣4.9t2.若小球的高度为4.9米,则小球的运动时间为 .15.如图,2016年里约奥运会上,某运动员在10米跳台跳水比赛时估测身体![]() 看成一点
看成一点![]() 在空中的运动路线是抛物线
在空中的运动路线是抛物线![]() 图中标出的数据为已知条件
图中标出的数据为已知条件![]() ,运动员在空中运动的最大高度离水面为 米
,运动员在空中运动的最大高度离水面为 米![]()
 16.矩形ABCD中,点P从点A出发,沿AB边以每秒1个单位的速度向B点运动,至B点停止;同时点Q也从A点出发,以同样的速度沿A-D-C-B的路径运动,至B点停止,在此过程中△APQ的面积y与运动时间t的函数关系图象如图所示,则m的值为
16.矩形ABCD中,点P从点A出发,沿AB边以每秒1个单位的速度向B点运动,至B点停止;同时点Q也从A点出发,以同样的速度沿A-D-C-B的路径运动,至B点停止,在此过程中△APQ的面积y与运动时间t的函数关系图象如图所示,则m的值为 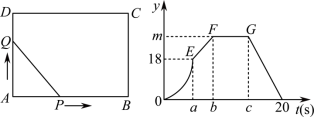 17.用
17.用![]() 的铁丝所围的长方形的面积
的铁丝所围的长方形的面积![]() 与长
与长![]() 的关系 .18.记抛物线C1:y=(x﹣2)2+3的顶点为A,抛物线C2:y=ax2+1(a<0)顶点是点B,且与x轴的正半轴交于点 C.当△ABC是直角三角形时,抛物线C2的解析式为 .19.抛物线y=x2﹣4x+3与x轴交于A、B,与y轴交于C,则△ABC的面积= .20.如图是一副眼镜镜片下半部分轮廓对应的两条抛物线关于y轴对称.AB//x轴,AB=4cm,最低点C在x轴上,高CH=1cm,BD=2cm则右轮廓线DFE所在抛物线的函数表达式为 (不用写x的取值范围).
的关系 .18.记抛物线C1:y=(x﹣2)2+3的顶点为A,抛物线C2:y=ax2+1(a<0)顶点是点B,且与x轴的正半轴交于点 C.当△ABC是直角三角形时,抛物线C2的解析式为 .19.抛物线y=x2﹣4x+3与x轴交于A、B,与y轴交于C,则△ABC的面积= .20.如图是一副眼镜镜片下半部分轮廓对应的两条抛物线关于y轴对称.AB//x轴,AB=4cm,最低点C在x轴上,高CH=1cm,BD=2cm则右轮廓线DFE所在抛物线的函数表达式为 (不用写x的取值范围).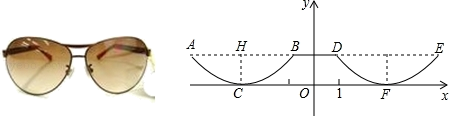 三、解答题21.某工艺厂设计了一款成本为10元/件的工艺品投放市场进行试销.经过调查,得到如下数据:销售单价x(元/件)…2030405060…每天销售量(y件)…500400300200100…(1)已知y是x的函数,请你分析它是我们学过的哪种函数,并求出函数关系式;(2)市物价部门规定,该工艺品销售单价最高不能超过35元/件,那么销售单价在什么范围时,工艺厂试销该工艺品每天获得的利润最大?最大利润是多少?22.某公司以30元/千克的价格收购一批农产品进行销售,为了得到日销售量y(千克)与销售价格x(元/千克)之间的关系,经过市场调查获得部分数据如下表:销售价格x(元/千克)354045日销售量y(千克)450300150(1)请你根据表中的数据用所学过的一次函数的知识直接写出y与x之间的函数表达式;并写出自变量x的取值范围.(2)销售价格定为多少元时,每天利润为2250元.(3)该公司应该如何确定这批农产品的销售价格,才能使日销售利润最大?23.如图,抛物线y=ax2+bx+c经过点A(0,﹣3)、B(﹣1,0)、C(2,﹣3),抛物线与x轴的另一交点为点E,点P为抛物线上一动点,设点P的横坐标为t.
三、解答题21.某工艺厂设计了一款成本为10元/件的工艺品投放市场进行试销.经过调查,得到如下数据:销售单价x(元/件)…2030405060…每天销售量(y件)…500400300200100…(1)已知y是x的函数,请你分析它是我们学过的哪种函数,并求出函数关系式;(2)市物价部门规定,该工艺品销售单价最高不能超过35元/件,那么销售单价在什么范围时,工艺厂试销该工艺品每天获得的利润最大?最大利润是多少?22.某公司以30元/千克的价格收购一批农产品进行销售,为了得到日销售量y(千克)与销售价格x(元/千克)之间的关系,经过市场调查获得部分数据如下表:销售价格x(元/千克)354045日销售量y(千克)450300150(1)请你根据表中的数据用所学过的一次函数的知识直接写出y与x之间的函数表达式;并写出自变量x的取值范围.(2)销售价格定为多少元时,每天利润为2250元.(3)该公司应该如何确定这批农产品的销售价格,才能使日销售利润最大?23.如图,抛物线y=ax2+bx+c经过点A(0,﹣3)、B(﹣1,0)、C(2,﹣3),抛物线与x轴的另一交点为点E,点P为抛物线上一动点,设点P的横坐标为t.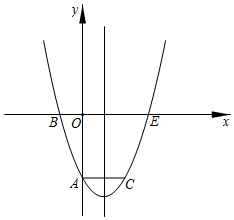 (1)求抛物线的解析式;(2)若点P在第一象限,点M为抛物线对称轴上一点,当四边形MBEP恰好是平行四边形时,求点P的坐标;(3)若点P在第四象限,连结PA、PE及AE,当t为何值时,△PAE的面积最大?最大面积是多少?(4)是否存在点P,使△PAE为以AE为直角边的直角三角形,若存在,直接写出点P的坐标;若不存在,请说明理由.24.为满足市场需求,某超市在“中秋”节前购进一种品牌月饼,每盒进价40元,超市规定每盒售价不得低于40元,根据以往销售经验,当售价定为每盒45元时,预计每天可以卖出700盒,每盒售价每提高1元,每天要少卖出20盒.(1)试求每天的销售量
(1)求抛物线的解析式;(2)若点P在第一象限,点M为抛物线对称轴上一点,当四边形MBEP恰好是平行四边形时,求点P的坐标;(3)若点P在第四象限,连结PA、PE及AE,当t为何值时,△PAE的面积最大?最大面积是多少?(4)是否存在点P,使△PAE为以AE为直角边的直角三角形,若存在,直接写出点P的坐标;若不存在,请说明理由.24.为满足市场需求,某超市在“中秋”节前购进一种品牌月饼,每盒进价40元,超市规定每盒售价不得低于40元,根据以往销售经验,当售价定为每盒45元时,预计每天可以卖出700盒,每盒售价每提高1元,每天要少卖出20盒.(1)试求每天的销售量![]() (盒)与售价
(盒)与售价![]() (元)之间的函数关系式;(2)如果要保证超市每天的利润为7980元,又要尽量减少库存,超市每天应该销售多少盒月饼?25.在平面直角坐标系中,已知抛物线
(元)之间的函数关系式;(2)如果要保证超市每天的利润为7980元,又要尽量减少库存,超市每天应该销售多少盒月饼?25.在平面直角坐标系中,已知抛物线![]() (b,c为常数)的顶点为P,等腰直角三角形ABC的顶点A的坐标为(0,﹣1),C的坐标为(4,3),直角顶点B在第四象限.
(b,c为常数)的顶点为P,等腰直角三角形ABC的顶点A的坐标为(0,﹣1),C的坐标为(4,3),直角顶点B在第四象限. (1)如图,若该抛物线过A,B两点,求该抛物线的函数表达式;(2)平移(1)中的抛物线,使顶点P在直线AC上滑动,且与AC交于另一点Q.(i)若点M在直线AC下方,且为平移前(1)中的抛物线上的点,当以M、P、Q三点为顶点的三角形是等腰直角三角形时,求出所有符合条件的点M的坐标;(ii)取BC的中点N,连接NP,BQ.试探究
(1)如图,若该抛物线过A,B两点,求该抛物线的函数表达式;(2)平移(1)中的抛物线,使顶点P在直线AC上滑动,且与AC交于另一点Q.(i)若点M在直线AC下方,且为平移前(1)中的抛物线上的点,当以M、P、Q三点为顶点的三角形是等腰直角三角形时,求出所有符合条件的点M的坐标;(ii)取BC的中点N,连接NP,BQ.试探究![]() 是否存在最大值.若存在,求出该最大值;若不存在,请说明理由.
是否存在最大值.若存在,求出该最大值;若不存在,请说明理由.
参考答案:1.D2.A3.C4.C5.C6.C7.D8.A9.B10.D11.![]() 12.1813.
12.1813.![]() 14.1s.15.
14.1s.15.![]() 16.2417.
16.2417.![]() /
/![]() 18.y=﹣x2+1或y=﹣
18.y=﹣x2+1或y=﹣![]() x2+119.320.
x2+119.320.![]() 21.(1)y=﹣10x+700(2)销售单价定为35元/件时,工艺厂试销该工艺品每天获得的利润最大为8750元22.(1)
21.(1)y=﹣10x+700(2)销售单价定为35元/件时,工艺厂试销该工艺品每天获得的利润最大为8750元22.(1)![]() (2)35或45(3)销售价格定为
(2)35或45(3)销售价格定为![]() 元,才能使日销售利润最大.23.(1)y=x2﹣2x﹣3;(2)P(4,5);(3)当t=
元,才能使日销售利润最大.23.(1)y=x2﹣2x﹣3;(2)P(4,5);(3)当t=![]() 时,S有最大值
时,S有最大值![]() ;(4)存在,理由,点P的坐标为:(﹣2,5)或(1,﹣4)24.(1)y=-20x+1600;(2)420盒.25.(1)
;(4)存在,理由,点P的坐标为:(﹣2,5)或(1,﹣4)24.(1)y=-20x+1600;(2)420盒.25.(1)![]() ;(2)(i)M1(4,﹣1),M2(﹣2,﹣7),M3(
;(2)(i)M1(4,﹣1),M2(﹣2,﹣7),M3(![]() ,
,![]() ),M4(
),M4(![]() ,
,![]() );(ii)存在,
);(ii)存在,![]() 的最大值为
的最大值为![]() .
.
相关试卷
这是一份初中华师大版26.3 实践与探索第3课时课时练习,共6页。
这是一份数学华师大版第26章 二次函数26.3 实践与探索练习题,共11页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。
这是一份华师大版九年级下册26.3 实践与探索同步训练题,共10页。试卷主要包含了32=0的根是,1),∴Q等内容,欢迎下载使用。









