


数学九年级上册2.频率与概率课后作业题
展开![]() 25.2.2频率与概率同步练习-华东师大版数学九年级上册
25.2.2频率与概率同步练习-华东师大版数学九年级上册
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.某射手在相同条件下进行射击训练,结果如下:
射击次数 | 10 | 20 | 40 | 50 | 100 | 200 | 500 | 1000 |
击中靶心的频数 | 9 | 19 | 37 | 45 | 89 | 181 | 449 | 901 |
击中靶心的频率 | 0.900 | 0.950 | 0.925 | 0.900 | 0.890 | 0.905 | 0.898 | 0.901 |
该射手击中靶心的概率的估计值是______(精确到0.01).( )
A.0.89 B.0.90 C.0.92 D.0.95
2.为了方便核酸检测,小刚将自己的核酸检测二维码打印在纸上,如图所示,为了估计图中黑色部分的面积,他在纸内随机掷点,经过大量重复试验,发现点落入黑色部分的频率稳定在0.5左右,测得二维码是边长为![]() 的正方形,据此可以估计黑色部分的面积约为( ).
的正方形,据此可以估计黑色部分的面积约为( ).

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.做任意抛掷一只纸杯的重复实验,获得如下数据:
抛掷总次数 | 杯口朝上 | 杯口朝下 | 横卧 |
100 | 0.21 | 0.38 | 0.41 |
200 | 0.22 | 0.38 | 0.40 |
500 | 0.22 | 0.38 | 0.40 |
 根据频率的稳定性,估计任意抛掷一只纸杯时杯口朝上的概率约是( )
根据频率的稳定性,估计任意抛掷一只纸杯时杯口朝上的概率约是( )
A.0.21 B.0.22 C.0.38 D.0.40
4.用频率估计概率,可以发现,某种幼树在一定条件下移植成活的概率为0.8,下列说法正确的是( )
A.移植10棵幼树,结果一定是“有8棵幼树成活”
B.移植1000棵幼树,结果一定是“800棵幼树成活”和“200棵幼树不成活”
C.移植10n棵幼树,恰好有“2n棵幼树不成活”
D.移植n棵幼树,当n越来越大时,移植成活幼树的频率会越来越稳定于0.8
5.小亮3分钟共投篮80次,进了64个球,则小亮进球的频率是( )
A.80 B.64 C.1.2 D.0.8
6.一个不透明的袋子中有1个红球,1个绿球和![]() 个白球, 这些球除颜外都相同. 从袋中随机摸出一个球, 记录其颜色, 然后放回. 大量重复该实验, 发现摸到绿球的频率稳定于
个白球, 这些球除颜外都相同. 从袋中随机摸出一个球, 记录其颜色, 然后放回. 大量重复该实验, 发现摸到绿球的频率稳定于![]() , 则白球的个数
, 则白球的个数![]() 的值可能是 ( )
的值可能是 ( )
A.1 B.2 C.4 D.5
7.布袋里有几百个乒乓球,想要估计球的数量,可以先从口袋中拿出一百个球,做上标记后放回布袋中混合均匀,若再从中任意摸出30个球,统计发现有标记的球有10个,则布袋中乒乓球数可能有( )
A.200个 B.300个 C.400个 D.500个
8.下列说法:①事件发生的概率与实验次数有关;②掷10次硬币,结果正面向上出现3次,反面向上出现7次,由此可得正面向上的概率是0.3;③如果事件A发生的概率为![]() ,那么大量反复做这种实验,事件A平均每100次发生5次.其中正确的个数为( )
,那么大量反复做这种实验,事件A平均每100次发生5次.其中正确的个数为( )
A.0个 B.1个 C.2个 D.3个
9.抛掷一枚质量分布均匀的硬币,出现“正面”和出现“反面”的机会均等,则下列说法正确的是( )
A.抛1000次的话一定会有500次出现“正面”
B.抛1000次的话一定会有500次出现“反面”
C.抛1000次的话出现“正面”和出现“反面”的次数都可能接近500次
D.抛1000次的话,出现“正面”和出现“反面”的次数无法预测,没有规律可循
10.某林业部门要考察某种幼树在一定条件下的移植成活率,下图是这种幼树在移植过程中成活情况的一组数据统计结果.下面三个推断:①当移植棵数是1500时,该幼树移植成活的棵数是1356,所以“移植成活”的概率是0.904;②随着移植棵数的增加,“移植成活”的频率总在0.880附近摆动,显示出一定的稳定性,可以估计这种幼树“移植成活”的概率是0.880;③若这种幼树“移植成活”的频率的平均值是0.875,则“移植成活”的概率是0.875.其中合理的是( )
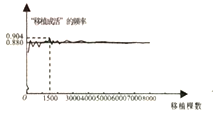
A.①③ B.②③ C.① D.②
二、填空题
11.为了估计湖里有多少条鱼,有如下方案:从湖里捕上![]() 条鱼做上标记,然后放回湖里,经过一段时间,待带标记的鱼完全混合于鱼群后,第二次再捕上
条鱼做上标记,然后放回湖里,经过一段时间,待带标记的鱼完全混合于鱼群后,第二次再捕上![]() 条,若其中带有标记的鱼有
条,若其中带有标记的鱼有![]() 条,那么估计湖里大约有 条鱼.
条,那么估计湖里大约有 条鱼.
12.在一个不透明的袋子里装有除颜色外完全相同的若干个黑球和6个白球,小明将其摇匀并随机摸出一个小球记录颜色后放回口袋,不断重复,共摸球400次,其中60次摸到白球,则盒中大约有黑球 个.
13.做任意抛掷一只纸杯的重复实验,部分数据如下表
抛掷次数 | 50 | 100 | 500 | 800 | 1500 | 3000 | 5000 |
杯口朝上的频率 | 0.1 | 0.15 | 0.2 | 0.21 | 0.22 | 0.22 | 0.22 |
根据上表,可估计任意抛掷一只纸杯,杯口朝上的概率约为 .
14.某玩具店进了一箱黑白两种颜色的塑料球![]() 个(除颜色外都相同),为了估计两种颜色的球各有多少个,将箱子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回箱子里,多次重复上述过程后,发现摸到黑球的频率在
个(除颜色外都相同),为了估计两种颜色的球各有多少个,将箱子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回箱子里,多次重复上述过程后,发现摸到黑球的频率在![]() 附近波动,据此可以估算黑球的个数约为 个.
附近波动,据此可以估算黑球的个数约为 个.
15.如表记录了一名球员在罚球线上投篮的结果.那么,这名球员投篮一次,投中的概率约为 (精确到0.1).
投篮次数(n) | 50 | 100 | 150 | 200 | 250 | 300 | 500 |
投中次数(m) | 28 | 60 | 78 | 104 | 123 | 152 | 251 |
投中频率(m/n) | 0.56 | 0.60 | 0.52 | 0.52 | 0.49 | 0.51 | 0.50 |
16.某玩具店进了一排黑白塑料球,共5箱,每箱的规格、数量都相同,其中每箱中装有黑白两种颜色的塑料球共3000个,为了估计每箱中两种颜色球的个数,随机抽查了一箱,将箱子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回箱子中,多次重复上述过程后,发现摸到黑球的概率在0.8附近波动,则此可以估计这批塑料球中黑球的总个数,请将黑球总个数用科学记数法表示约为 个.
17.在一个不透明的袋子中,装有红球和白球共20个,这些球除颜色外都相同,搅匀后从中任意摸出一个球记下颜色,再把它放回袋子中,不断重复实验,统计结果显示,随着实验次数越来越大,摸到红球的频率逐渐稳定在 0.3左右,则据此估计袋子中大约有白球 个.
18.小刚向盒中放了![]() 个黑球,摇匀后从中随机摸出一个球记下颜色,再把它放回盒中,不断重复,共摸球
个黑球,摇匀后从中随机摸出一个球记下颜色,再把它放回盒中,不断重复,共摸球![]() 次,其中
次,其中![]() 次摸到黑球,估计盒中大约有白球 .
次摸到黑球,估计盒中大约有白球 .
19.所谓频率,是在相同条件下进行重复试验时,事件发生的次数与 的比值,其本身是随机的,在试验前不能够确定,且随着试验的不同而发生改变. 而一个随机事件发生的概率是确定的常数,是客观存在的,与试验次数 .
从以上角度上讲,频率与概率是有区别的,但在大量的重复试验中,随机事件发生的频率会呈现出明显的规律性:随着试验次数的增加,频率将会越来越集中在一个 附近,具有 性,即试验频率稳定于其理论概率.
20.将容量为100的样本分成3个组,第一组的频数是35,第二组的频率是0.28,那么第三组的频率是 .
三、解答题
21.新冠疫情期间,某校有“录播”和“直播”两种教学方式供学生自主选择其中一种进行居家线上学习.为了了解该校学生线上学习参与度情况,从选择这两种教学方式的学生中,分别随机抽取50名进行调查,调查结果如表(数据分组包含左端值不包含右端值).
|
|
|
|
|
录播 | 5 | 18 | 14 | 13 |
直播 | 2 | 15 | 21 | 12 |
(1)从选择教学方式为“录播”的学生中任意抽取1名学生,试估计该生的参与度不低于![]() 的概率;
的概率;
(2)若该校共有1200名学生,选择“录播”和“直播”的人数之比为![]() ,试估计选择“录播”或“直播”参与度均在
,试估计选择“录播”或“直播”参与度均在![]() 以下的共有多少人?
以下的共有多少人?
22.一只不透明的口袋中放着若干个黄球和绿球,这两种球除了颜色之外没有其它任何区别,袋中的球已经搅匀,从口袋中取出一个球取出黄球的概率为![]() .
.
(1)取出绿球的概率是多少?
(2)如果袋中的黄球有12个,那么袋中的绿球有多少个?
23.某位篮球运动员在同样的条件下进行投篮练习,结果如下表:
投篮次数 |
|
|
|
|
|
|
|
进球次数 |
|
|
|
|
|
|
|
进球频率 | ________ | ________ | ________ | ________ | ________ | ________ | ________ |
![]() 将上表补充完整;
将上表补充完整;
![]() 这位运动员投篮一次,进球的概率约是多少?
这位运动员投篮一次,进球的概率约是多少?
![]() 若这位运动员投篮
若这位运动员投篮![]() 次,必定会投进
次,必定会投进![]() 次吗?为什么?
次吗?为什么?
24.为了准备体育艺术节的比赛,某篮球运动员在进行定点罚球训练,下表是部分训练记录:
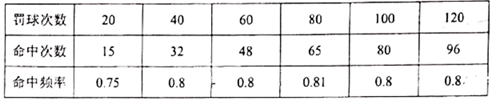
(1)根据上表:估计该运动员罚球命中的概率是 ;
(2)根据上表分析,如果该运动员在一次比赛中共获得![]() 次罚球机会(每次罚球投掷
次罚球机会(每次罚球投掷![]() 次,每命中一次得
次,每命中一次得![]() 分),估计他罚球能得多少分,请说明理由.
分),估计他罚球能得多少分,请说明理由.
25.自2009年以来,“中国·兴化千垛菜花旅游节”享誉全国.“河有万湾多碧水,田无一垛不黄花”所描绘的就是我市发达的油菜种植业.为了解某品种油菜籽的发芽情况,农业部门从该品种油菜籽中抽取了6批,在相同条件下进行发芽试验,有关数据如下:
批次 | 1 | 2 | 3 | 4 | 5 | 6 |
油菜籽粒数 | 100 | 400 | 800 | 1000 | 2000 | 5000 |
发芽油菜籽粒数 |
| 318 | 652 | 793 | 1604 | 4005 |
发芽频率 | 0.850 | 0.795 | 0.815 | 0.793 |
| 0.801 |
(1)分别求![]() 和
和![]() 的值;
的值;
(2)请根据以上数据,直接写出该品种油菜籽发芽概率的估计值(精确到0.1);
(3)农业部门抽取的第7批油菜籽共有8000粒.请你根据问题(2)的结果,通过计算来估计第7批油菜籽在相同条件下进行发芽试验时的发芽粒数.
参考答案:
1.B
2.D
3.B
4.D
5.D
6.B
7.B
8.B
9.C
10.D
11.2000
12.34
13.0.22
14.![]()
15.0.5
16.1.2×104
17.14
18.32
19. 试验总次数 无关 常数 稳定
20.0.37
21.(1)![]() ;(2)75人
;(2)75人
22.(1)取出绿球的概率是![]() ;
;
(2)绿球有18个
23.![]() 答案为:
答案为:![]() ;
;![]() ;
;![]() ;
;![]() ;
;![]() ;
;![]() ;
;![]() ;
;![]() ;
;![]() 这位运动员投篮
这位运动员投篮![]() 次,不一定会投进
次,不一定会投进![]() 次,理由详见解析.
次,理由详见解析.
24.(1)0.8;(2)估计他能得![]() 分.
分.
25.(1)![]() ,
,![]()
(2)该品种油菜籽发芽概率的估计值为0.8
(3)估计第7批油菜籽在相同条件下进行发芽试验时的发芽粒数为6400粒
初二数学频率与概率的关系同步练习及答案: 这是一份初二数学频率与概率的关系同步练习及答案,共8页。试卷主要包含了3和0,6%,24,不公平,公平,P=, ; ; ;等内容,欢迎下载使用。
华师大版九年级上册第24章 解直角三角形24.1 测量习题: 这是一份华师大版九年级上册第24章 解直角三角形24.1 测量习题,共7页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。
初中数学华师大版九年级上册2.频率与概率巩固练习: 这是一份初中数学华师大版九年级上册2.频率与概率巩固练习,文件包含频率与概率-九年级数学上册同步培优题典解析版华师大版docx、频率与概率-九年级数学上册同步培优题典原卷版华师大版docx等2份试卷配套教学资源,其中试卷共13页, 欢迎下载使用。














