浙教版2023年八年级上册第2章《特殊三角形》单元检测卷
展开
这是一份浙教版2023年八年级上册第2章《特殊三角形》单元检测卷,共5页。
浙教版2023年八年级上册第2章《特殊三角形》单元检测卷一.选择题(共10小题,满分30分,每小题3分)1.下列图形中不是轴对称图形的是( )A.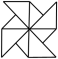 B.
B.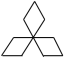 C.
C.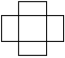 D.
D.![]() 2.在Rt△ABC中,若一个锐角等于40°,则另一个锐角的度数为( )A.40° B.45° C.50° D.60°3.在△ABC中,AB=AC,∠A=50°,则∠B的度数是( )A.50° B.65° C.80° D.130°4.如图,在△ABC中,AB=AC,AD是∠BAC的平分线,若BD=5,则CD等于( )
2.在Rt△ABC中,若一个锐角等于40°,则另一个锐角的度数为( )A.40° B.45° C.50° D.60°3.在△ABC中,AB=AC,∠A=50°,则∠B的度数是( )A.50° B.65° C.80° D.130°4.如图,在△ABC中,AB=AC,AD是∠BAC的平分线,若BD=5,则CD等于( )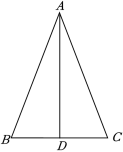 A.3 B.4 C.5 D.65.如图,若要用“HL”证明Rt△ABC≌Rt△ABD,则还需补充条件( )
A.3 B.4 C.5 D.65.如图,若要用“HL”证明Rt△ABC≌Rt△ABD,则还需补充条件( )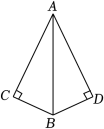 A.∠BAC=∠BAD B.AC=AD或BC=BD C.∠ABC=∠ABD D.以上都不正确6.下列命题中,其逆命题是真命题的是( )A.同旁内角互补,两直线平行 B.如果两个角是直角,那么它们相等 C.若两实数相等,则这两个数的绝对值一定相等 D.全等三角形的对应角相等7.在Rt△ABC中,斜边BC=10,则AB2+AC2=( )A.10 B.20 C.50 D.1008.已知等腰三角形的两条边长分别为2和5,则它的周长为( )A.9 B.12 C.9或12 D.59.如图,在△ABC中,AB=AC,∠A=36°,D、E两点分别在边AC、BC上,BD平分∠ABC,DE∥AB.图中的等腰三角形共有( )
A.∠BAC=∠BAD B.AC=AD或BC=BD C.∠ABC=∠ABD D.以上都不正确6.下列命题中,其逆命题是真命题的是( )A.同旁内角互补,两直线平行 B.如果两个角是直角,那么它们相等 C.若两实数相等,则这两个数的绝对值一定相等 D.全等三角形的对应角相等7.在Rt△ABC中,斜边BC=10,则AB2+AC2=( )A.10 B.20 C.50 D.1008.已知等腰三角形的两条边长分别为2和5,则它的周长为( )A.9 B.12 C.9或12 D.59.如图,在△ABC中,AB=AC,∠A=36°,D、E两点分别在边AC、BC上,BD平分∠ABC,DE∥AB.图中的等腰三角形共有( ) A.3个 B.4个 C.5个 D.6个10.如图,在△DEF中,∠D=90°,DG:GE=1:3,GE=GF,Q是EF上一动点,过点Q作QM⊥DE于M,QN⊥GF于N,
A.3个 B.4个 C.5个 D.6个10.如图,在△DEF中,∠D=90°,DG:GE=1:3,GE=GF,Q是EF上一动点,过点Q作QM⊥DE于M,QN⊥GF于N,![]() ,则QM+QN的长是( )
,则QM+QN的长是( )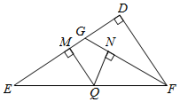 A.4
A.4![]() B.3
B.3![]() C.4 D.2
C.4 D.2![]() 二.填空题(共6小题,满分18分,每小题3分)11.命题“直角三角形两条直角边的平方和等于斜边的平方”的逆命题是 .12.如图,在△ABC中,AB=AC,AB的垂直平分线交AB于点D,交AC于点E.已知△BCE的周长为10cm,且BC=4cm,则BD的长为 .
二.填空题(共6小题,满分18分,每小题3分)11.命题“直角三角形两条直角边的平方和等于斜边的平方”的逆命题是 .12.如图,在△ABC中,AB=AC,AB的垂直平分线交AB于点D,交AC于点E.已知△BCE的周长为10cm,且BC=4cm,则BD的长为 .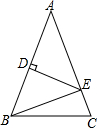 13.如图,Rt△ABC的直角边AB在数轴上,点A表示的实数为0,以A为圆心,AC的长为半径作弧交数轴的负半轴于点D.若CB=1,AB=2,则点D表示的实数为 .
13.如图,Rt△ABC的直角边AB在数轴上,点A表示的实数为0,以A为圆心,AC的长为半径作弧交数轴的负半轴于点D.若CB=1,AB=2,则点D表示的实数为 .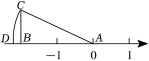 14.用三根木棒首尾相连围成一个等腰三角形,其中两根木棒的长度分别为3cm和6cm,则第三根木棒长为 cm.15.如图,有一个三级台阶,每一级的长、宽、高分别是50cm、30cm、10cm,点A和点B是这个台阶的两个相对的顶点,有一只壁虎从A点出发,沿着台阶面爬向B点去吃可口的食物;请你想一想,这只壁虎至少需要爬 cm.
14.用三根木棒首尾相连围成一个等腰三角形,其中两根木棒的长度分别为3cm和6cm,则第三根木棒长为 cm.15.如图,有一个三级台阶,每一级的长、宽、高分别是50cm、30cm、10cm,点A和点B是这个台阶的两个相对的顶点,有一只壁虎从A点出发,沿着台阶面爬向B点去吃可口的食物;请你想一想,这只壁虎至少需要爬 cm.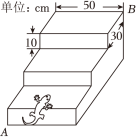 16.如图,在等边△ABC中,点D、E分别是AB、BC的中点,AD=6,点P是AD上的一动点,则PE+PB的最小值为 .
16.如图,在等边△ABC中,点D、E分别是AB、BC的中点,AD=6,点P是AD上的一动点,则PE+PB的最小值为 .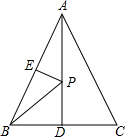 三.解答题(共7小题,满分52分)17.(6分)如图,在△ABC中,AB=AC,AD是BC边上的中线,BE⊥AC于E,求证:∠EBC=∠DAC.
三.解答题(共7小题,满分52分)17.(6分)如图,在△ABC中,AB=AC,AD是BC边上的中线,BE⊥AC于E,求证:∠EBC=∠DAC.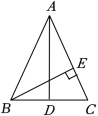 18.(6分)如图,在△ABC中,AC=BC,直线l经过顶点C,过A,B两点分别作l的垂线AE,BF,E,F为垂足,AE=CF.求证:∠ACB=90°.
18.(6分)如图,在△ABC中,AC=BC,直线l经过顶点C,过A,B两点分别作l的垂线AE,BF,E,F为垂足,AE=CF.求证:∠ACB=90°.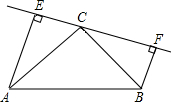 19.(7分)如图,在△ABC中,CD⊥AB于点D,AC=20,BC=15,DB=9.(1)求DC的长; (2)求AB的长; (3)求∠ACB的度数.
19.(7分)如图,在△ABC中,CD⊥AB于点D,AC=20,BC=15,DB=9.(1)求DC的长; (2)求AB的长; (3)求∠ACB的度数.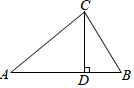 20.(7分)如图所示,在△ABC中,BE平分∠ABC,DE∥BC.(1)求证:△BDE是等腰三角形;(2)若∠A=35°,∠C=70°,求∠BDE的度数.
20.(7分)如图所示,在△ABC中,BE平分∠ABC,DE∥BC.(1)求证:△BDE是等腰三角形;(2)若∠A=35°,∠C=70°,求∠BDE的度数.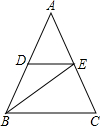 21.(8分)如图,在正方形网格中,每个小正方形的边长都为1,网格中有一个格点△ABC(即三角形的顶点都在格点上).(1)在图中画出△ABC关于直线l对称的△A1B1C1;(2)在直线l上找出点P,使得△PBC周长最小,在图中标出点P的位置;(3)已知点D在格点上,且△BCD 和△BCA 全等,请画出所有满足条件的△BCD (点D与点A不重合).
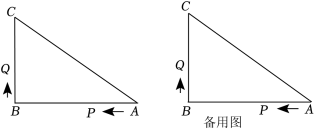
21.(8分)如图,在正方形网格中,每个小正方形的边长都为1,网格中有一个格点△ABC(即三角形的顶点都在格点上).(1)在图中画出△ABC关于直线l对称的△A1B1C1;(2)在直线l上找出点P,使得△PBC周长最小,在图中标出点P的位置;(3)已知点D在格点上,且△BCD 和△BCA 全等,请画出所有满足条件的△BCD (点D与点A不重合).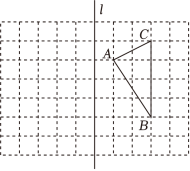 22.(8分)阅读与思考阅读下列材料,完成后面的任务:赵爽“弦圈”与完全平方公式三国时期吴国的数学家赵爽创建了一幅“弦图”,利用面积法给出了勾股定理的证明.实际上,该“弦图”与完全平方公式有着密切的关系,如图2,这是由8个全等的直角边长分别为a,b,斜边长为c的三角形拼成的“弦图”.由图可知,1个大正方形ABCD的面积=8个直角三角形的面积+1个小正方形PQMN的面积.任务:(1)在图2中,正方形ABCD的面积可表示为 ,正方形PQMN的面积可表示为 .(用含a,b的式子表示)(2)根据S正方形ABCD=8S直角三角形+S正方形PQMN,可得(a+b)2,ab,(a﹣b)2之间的关系为 .(3)根据(2)中的等量关系,解决问题:已知a+b=5,ab=4,求(a﹣b)2的值.
22.(8分)阅读与思考阅读下列材料,完成后面的任务:赵爽“弦圈”与完全平方公式三国时期吴国的数学家赵爽创建了一幅“弦图”,利用面积法给出了勾股定理的证明.实际上,该“弦图”与完全平方公式有着密切的关系,如图2,这是由8个全等的直角边长分别为a,b,斜边长为c的三角形拼成的“弦图”.由图可知,1个大正方形ABCD的面积=8个直角三角形的面积+1个小正方形PQMN的面积.任务:(1)在图2中,正方形ABCD的面积可表示为 ,正方形PQMN的面积可表示为 .(用含a,b的式子表示)(2)根据S正方形ABCD=8S直角三角形+S正方形PQMN,可得(a+b)2,ab,(a﹣b)2之间的关系为 .(3)根据(2)中的等量关系,解决问题:已知a+b=5,ab=4,求(a﹣b)2的值.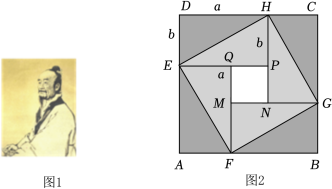 23.(10分)如图,在△ABC中,∠B=90°,AB=16cm,BC=12cm,P、Q是△ABC边上的两个动点,其中点P从点A出发,沿A→B方向运动,速度为每秒2cm;点Q从点B出发,沿B→C→A方向运动,速度为每秒4cm;两点同时开始运动,设运动时间为t秒.(1)①Rt△ABC斜边AC上的高为 ;②当t=3时,PQ的长为 ;(2)当点Q在边BC上运动时,出发几秒钟后,△BPQ是等腰三角形?(3)当点Q在边AC上运动时,直接写出所有能使△BCQ成为等腰三角形的t的值.
23.(10分)如图,在△ABC中,∠B=90°,AB=16cm,BC=12cm,P、Q是△ABC边上的两个动点,其中点P从点A出发,沿A→B方向运动,速度为每秒2cm;点Q从点B出发,沿B→C→A方向运动,速度为每秒4cm;两点同时开始运动,设运动时间为t秒.(1)①Rt△ABC斜边AC上的高为 ;②当t=3时,PQ的长为 ;(2)当点Q在边BC上运动时,出发几秒钟后,△BPQ是等腰三角形?(3)当点Q在边AC上运动时,直接写出所有能使△BCQ成为等腰三角形的t的值.