人教版九年级上册数学活动同步测试题

这是一份人教版九年级上册数学活动同步测试题，文件包含九年级数学上册245圆重点定理和辅助圆模型50题-重要笔记2022-2023学年九年级数学上册重要考点精讲精练人教版原卷版docx、九年级数学上册245圆重点定理和辅助圆模型50题-重要笔记2022-2023学年九年级数学上册重要考点精讲精练人教版解析版docx等2份试卷配套教学资源，其中试卷共60页， 欢迎下载使用。
24.5 圆重点定理和辅助圆模型（50题）


题型1：垂径定理
1．如图，BC是⊙O的直径，AD⊥BC，∠ABC＝25°，则弧CD的度数（　　）

A．50° B．25° C．100° D．65°
【分析】连接OA，根据圆周角定理可得∠AOC的度数，从而求出的度数，然后再利用垂径定理可得＝，即可解答．
【解答】解：连接OA，
∵∠ABC＝25°，
∴∠AOC＝2∠ABC＝50°，
∴的度数为50°，
∴BC是⊙O的直径，AD⊥BC，
∴＝，
∴弧CD的度数为50°，
故选：A．
【点评】本题考查了圆周角定理，圆心角、弧、弦的关系，垂径定理，熟练掌握圆周角定理，以及垂径定理是解题的关键．
2．如图，在⊙O中，弦AB的长是cm，弦AB的弦心距为6cm，E是⊙O优弧AEB上一点．则∠AEB的度数为（　　）

A．60° B．45° C．30° D．80°
【分析】连接OA，OB，利用垂径定理求出AC，然后在Rt△AOC中，利用锐角三角函数求出∠OAC，从而求出∠AOB，最后利用圆周角定理求出∠AEB进行计算即可解答．
【解答】解：连接OA，OB，

∵OC⊥AB，
∴AC＝AB＝6cm，
在Rt△AOC中，OC＝6cm，
∴tan∠OAC＝＝＝，
∴∠OAC＝30°，
∵OA＝OB，
∴∠OAB＝∠OBA＝30°，
∴∠AOB＝180°﹣∠OAB﹣∠OBA＝120°，
∴∠AEB＝∠AOB＝60°，
故选：A．
【点评】本题考查了解直角三角形，圆周角定理，垂径定理，熟练掌握圆周角定理，垂径定理是解题的关键．
4．如图，已知⊙O的直径CD垂直于弦AB，垂足为点E，∠D＝22.5°，AB＝8，则DE的长为 　 　．

【分析】连接OB，根据圆周角定理可得∠BOC＝45°，再利用垂径定理可得∠OEB＝90°，BE＝AB＝4，从而可得OE＝BE＝4，OB＝BE＝4，进行计算即可解答．
【解答】解：连接OB，

∵∠D＝22.5°，
∴∠BOC＝2∠D＝45°，
∵直径CD⊥AB，
∴∠OEB＝90°，BE＝AB＝4，
∴∠OBE＝90°﹣∠BOE＝45°，
∴OE＝BE＝4，OB＝BE＝4，
∴OD＝OB＝4，
∴DE＝OD+OE＝4+4，
故答案为：4+4．
【点评】本题考查了圆周角定理，垂径定理，勾股定理，熟练掌握圆周角定理，以及垂径定理是解题的关键．
5．如图，AB是⊙O的弦，连接BO，作AC⊥BO交BO的延长线于点C，已知OC＝，BO＝2，点D是的中点，连接CD，则CD的长为 　　．

【分析】先求∠CAO＝30°，再证△OAD是等边三角形，最后在Rt△ACD中，用勾股定理求解．
【解答】解：如图，连接OA、OD、AD，
∵OA＝0B＝2，OC＝，AC⊥BO，
∴∠OAC＝30°，∠AOC＝60°，
∴∠OAB＝∠OBA＝30°，
在Rt△ABC中，
AC＝，
∵点D是，
∴∠AOD＝∠BOD＝60°，
∴△AOD为等边三角形，
∴AD＝AO＝2，
在Rt△ACD中，
CD＝＝．
故答案为：．

【点评】本题考查了垂径定理，圆周角定理，勾股定理等知识，解题的关键是添加辅助线，构造直角三角形．
6．如图，在⊙O中，AB，AC为弦，CD为直径，AB⊥CD于E，BF⊥AC于F，BF与CD相交于G．
（1）求证：ED＝EG；
（2）若AB＝8，OG＝1，求⊙O的半径．

【分析】（1）连接BD，容易得到∠GBE和∠DBE相等，利用ASA证明△BGE和△BDE全等即可；
（2）连接OA，设OA＝r，则DG＝r+1，根据ED＝EG容易求出OE＝，再根据垂径定理求出AE的值，最后在Rt△OAE中根据勾股定理求出r的值即可．
【解答】（1）证明：如图：连接BD，

∵AB⊥CD于E，BF⊥AC于F，
∴∠CFG＝∠GEB，
∵∠CGF＝∠BGE，
∴∠C＝∠GBE，
∵∠C＝∠DBE，
∴∠GBE＝∠DBE，
∵AB⊥CD于E，
∴∠GEB＝∠DEB，
在△GBE和△DBE中，
，
∴△BGE≌△BDE（ASA），
∴ED＝EG．
（2）解：如图：

连接OA，设OA＝r，则DG＝r+1，
由（1）可知ED＝EG，
∴OE＝，
∵AB⊥CD于E，AB＝8，
∴AE＝BE＝4，
∴在Rt△OAE中，根据勾股定理得：OE2+AE2＝OA2，
即（）2+42＝r2，
解得：r＝，
即⊙O的半径为．
【点评】本题结合勾股定理和全等三角形的证明考查了垂径定理的应用，垂直于弦的直径平分弦，并且平分弦所对的优弧和劣弧．
7．如图，⊙O的半径为4，△ABC是⊙O的内接三角形，连接OB、OC．若∠BAC与∠BOC互补，求弦BC的长．

【分析】首先过点O作OD⊥BC于D，由垂径定理可得BC＝2BD，又由圆周角定理，可求得∠BOC的度数，然后根据等腰三角形的性质，求得∠OBC的度数，利用余弦函数，即可求得答案．
【解答】解：如图，过点O作OD⊥BC于D，
则BC＝2BD，
∵△ABC内接于⊙O，∠BAC与∠BOC互补，
∴∠BOC＝2∠A，∠BOC+∠A＝180°，
∴∠BOC＝120°，
∵OB＝OC，
∴∠OBC＝∠OCB＝（180°﹣∠BOC）＝30°，
∵⊙O的半径为4，
∴BD＝OB•cos∠OBC＝4×＝2，
∴BC＝4．

【点评】本题考查了圆周角定理、垂径定理、等腰三角形的性质以及三角函数等知识．注意掌握辅助线的作法．

题型2：圆周角定理
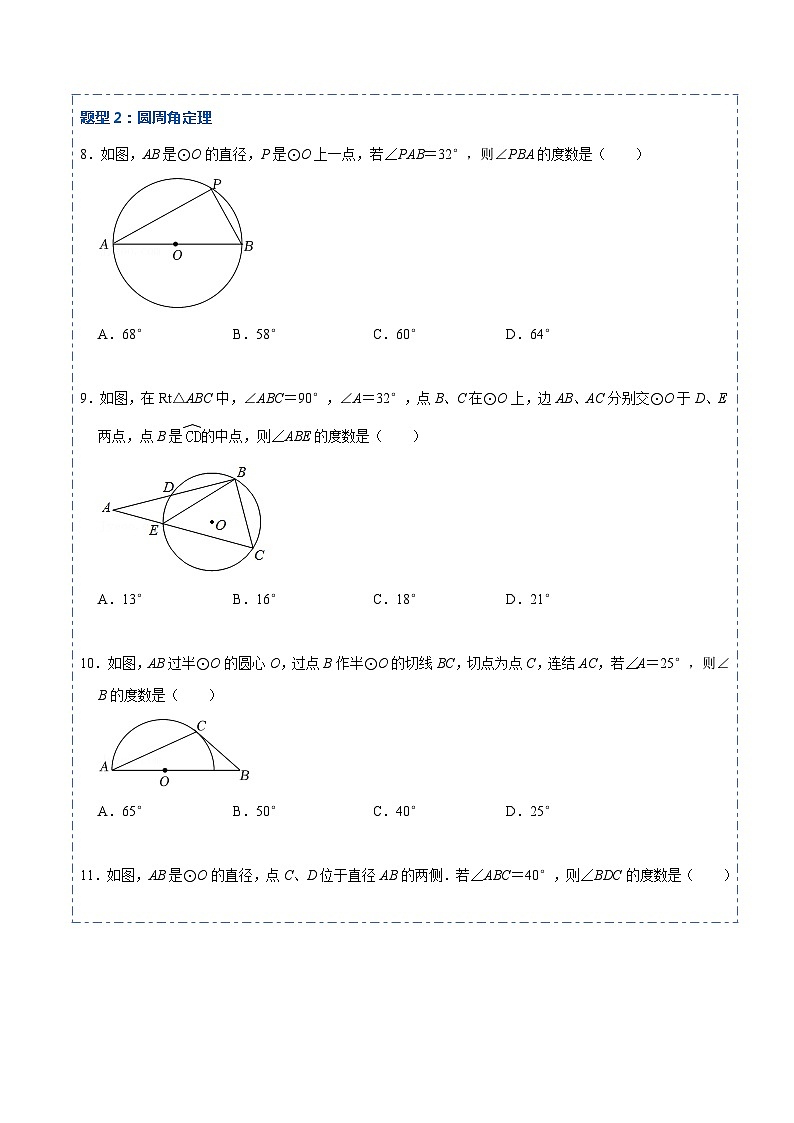
8．如图，AB是⊙O的直径，P是⊙O上一点，若∠PAB＝32°，则∠PBA的度数是（　　）

A．68° B．58° C．60° D．64°
【分析】根据直径所对的圆周角是直角可得∠APB＝90°，然后利用直角三角形的两个锐角互余，进行计算即可解答．
【解答】解：∵AB是⊙O的直径，
∴∠APB＝90°，
∵∠PAB＝32°，
∴∠PBA＝90°﹣∠PAB＝58°，
故选：B．
【点评】本题考查了圆周角定理，熟练掌握圆周角定理是解题的关键．
9．如图，在Rt△ABC中，∠ABC＝90°，∠A＝32°，点B、C在⊙O上，边AB、AC分别交⊙O于D、E两点，点B是的中点，则∠ABE的度数是（　　）

A．13° B．16° C．18° D．21°
【分析】连接CD，根据已知可得＝，从而可得BD＝BC，进而可得∠BDC＝∠BCD＝45°，然后利用直角三角形的两个锐角互余可得∠ACB＝58°，从而求出∠DCE＝13°，最后根据同弧所对的圆周角相等即可解答．
【解答】解：连接CD，

∵点B是的中点，
∴＝，
∴BD＝BC，
∵∠ABC＝90°，
∴∠BDC＝∠BCD＝45°，
∵∠A＝32°，
∴∠ACB＝90°﹣∠A＝58°，
∴∠DCE＝∠ACB﹣∠DCB＝13°，
∴∠ABE＝∠DCE＝13°，
故选：A．
【点评】本题考查了圆周角定理，根据题目的已知条件并结合图形添加适当的辅助线是解题的关键．
10．如图，AB过半⊙O的圆心O，过点B作半⊙O的切线BC，切点为点C，连结AC，若∠A＝25°，则∠B的度数是（　　）

A．65° B．50° C．40° D．25°
【分析】连接OC，根据切线的性质可得∠OCB＝90°，再根据圆周角定理可得∠BOC＝50°，然后利用直角三角形的两个锐角互余进行计算即可解答．
【解答】解：连接OC，

∵BC与半⊙O相切于点C，
∴∠OCB＝90°，
∵∠A＝25°，
∴∠BOC＝2∠A＝50°，
∴∠B＝90°﹣∠BOC＝40°，
故选：C．

【点评】本题考查了切线的性质，圆周角定理，根据题目的已知条件并结合图形添加适当的辅助线是解题的关键．
11．如图，AB是⊙O的直径，点C、D位于直径AB的两侧．若∠ABC＝40°，则∠BDC的度数是（　　）


A．50° B．40° C．60° D．45°
【分析】根据同弧所对的圆周角相等可得∠ADC＝40°，再根据直径所对的圆周角是直角可得答案．
【解答】解：∵＝，
∴∠ADC＝∠ABC＝40°，
∵AB为⊙O的直径，
∴∠ADB＝90°，
∴∠BDC＝∠ADB﹣∠ADC＝90°﹣40°＝50°．
故选：A．
【点评】本题考查圆周角定理，熟练掌握圆周角定理以及推论是解题关键．
12．如图，点A为⊙O上一点，AB为⊙O的切线，∠CAB＝30°，直径CD＝2，则劣弧AD的长是 　 　．

【分析】连接OA，根据切线的性质可得∠OAB＝90°，从而可求出∠OAC＝60°，然后利用等腰三角形的性质可求出∠C＝60°，再利用圆周角定理求出∠AOD的度数，最后利用弧长公式进行计算即可解答．
【解答】解：连接OA，

∵AB为⊙O的切线，
∴∠OAB＝90°，
∵∠CAB＝30°，
∴∠OAC＝∠OAB﹣∠CAB＝60°，
∵OA＝OC，
∴∠OAC＝∠C＝60°，
∴∠AOD＝2∠C＝120°，
∵直径CD＝2，
∴OD＝CD＝1，
∴劣弧AD的长＝＝π，
故答案为：π．

【点评】本题考查了切线的性质，圆周角定理，弧长的计算，等腰三角形的性质，熟练掌握切线的性质，以及圆周角定理是解题的关键．
13．如图，点A，B，C是⊙O上的三点．若∠AOC＝90°，∠BAC＝30°，则∠AOB的度数为 　．

【分析】由圆周角定理可得∠BOC＝2∠BAC＝60°，继而∠AOB＝∠AOC﹣∠BOC＝90°﹣60°＝30°．
【解答】解：∵∠BAC与∠BOC所对弧为，
由圆周角定理可知：∠BOC＝2∠BAC＝60°，
又∵∠AOC＝90°，
∴∠AOB＝∠AOC﹣∠BOC＝90°﹣60°＝30°．
故答案为：30°．
【点评】本题主要考查了圆周角定理，熟练运用圆周角定理是解题关键．
14．如图，AB是⊙O的直径，点C、D在⊙O上，且在AB异侧，连接OC、CD、DA．若∠BOC＝130°，则∠D的大小是 　 　．

【分析】根据平角定义求出∠AOC＝50°，再利用圆周角定理可得∠D＝∠AOC，进行计算即可解答．
【解答】解：∵∠BOC＝130°，
∴∠AOC＝180°﹣∠BOC＝50°，
∴∠D＝∠AOC＝25°，
故答案为：25°．
【点评】本题考查了圆周角定理，圆心角、弧、弦的关系，熟练掌握圆周角定理是解题的关键．
15．如图，已知点A、B、C、D在圆O上，，∠CAD＝35°，∠ACD＝60°，则∠AOB＝　 　．

【分析】先求出∠ADB的度数，在根据圆周角定理即可求出∠AOB的度数．
【解答】解：∵，∠CAD＝35°，
∴∠CDB＝∠CAD＝35°，
∵∠CAD＝35°，∠ACD＝60°，
∴∠ADC＝85°，
∴∠ADB＝∠ADC﹣∠CDB＝50°，
∴∠AOB＝2×50°＝100°．
故答案为：100°．
【点评】本题考查了圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．
16．如图，AB是⊙O的直径，C为⊙O上一点，AD和过点C的切线CD互相垂直，垂足为D．
求证：∠CAD＝∠CAB；


【分析】连接OC，根据切线的性质可得∠DCO＝90°，再根据垂直定义可得∠ADC＝90°，从而可得AD∥OC，然后根据平行线和等腰三角形的性质，可证AC平分∠DAB，即可解答；

【解答】（1）证明：连接OC，

∵CD是⊙O的切线，点C为切点，
∴∠DCO＝90°，
∵AD⊥CD，
∴∠ADC＝90°，
∴∠ADC+∠DCO＝180°，
∴AD∥OC，
∴∠DAC＝∠ACO，
∵OA＝OC，
∴∠OAC＝∠ACO，
∴∠CAD＝∠CAB；


题型3：切线长定理
18．如图，从⊙O外一点P引圆的两条切线PA，PB，切点分别是A，B，若∠APB＝60°，PA＝5，则弦AB的长是（　　）

A． B． C．5 D．5
【分析】根据切线长定理得到PA＝PB，根据等边三角形的性质解答即可．
【解答】解：∵PA，PB为⊙O的两条切线，
∴PA＝PB，
∵∠APB＝60°，
∴△PAB为等边三角形，
∴AB＝PA＝5，
故选：C．
【点评】本题考查的是切线长定理、等边三角形的判定和性质，得出△PAB是等边三角形是解题的关键．
19．如图，直线AB、CD、BC分别与⊙O相切于E、F、G，且AB∥CD，若OB＝6cm，OC＝8cm，则BE+CG的长等于（　　）

A．13 B．12 C．11 D．10
【分析】根据平行线的性质以及切线长定理，即可证明∠BOC＝90°，再根据勾股定理即可求得BC的长，再结合切线长定理即可求解．
【解答】解：∵AB∥CD，
∴∠ABC+∠BCD＝180°，
∵CD、BC，AB分别与⊙O相切于G、F、E，
∴∠OBC＝∠ABC，∠OCB＝∠BCD，BE＝BF，CG＝CF，
∴∠OBC+∠OCB＝90°，
∴∠BOC＝90°，
∴BC＝＝10，
∴BE+CG＝10（cm）．
故选：D．
【点评】此题主要是考查了切线长定理．从圆外一点引圆的两条切线，它们的切线长相等，且圆心和这点的连线平分两条切线的夹角．
20．如图，在Rt△ABC中，AC＝5，BC＝12，⊙O分别与边AB，AC相切，切点分别为E，C，则⊙O的半径是（　　）

A． B． C． D．
【分析】根据切线长定理得AE＝AC，根据勾股定理得AB的长，从而得到BE的长，再利用切割线定理得BE2＝BD•BC，从而可求得BD的长，也就得到了半径的长．
【解答】解：∵AE＝AC＝5，AC＝5，BC＝12，
∴AB＝13，
∴BE＝8；
∵BE2＝BD•BC，
∴BD＝，
∴CD＝，
∴圆的半径是，
故选：A．
【点评】此题综合运用了切线长定理、勾股定理和切割线定理．
21．如图，三个半径为的圆两两外切，且△ABC的每一边都与其中的两个圆相切，那么△ABC的周长是（　　）

A．12+6 B．18+6 C．18+12 D．12+12
【分析】从各圆心向边作垂线，由题意知△ABC是等边三角形，BD是∠EBF的平分线，可求得BE＝BF＝DEcot30°＝3，AW＝AS＝CG＝CH＝3；再根据四边形WFDR，SGTR，THED是矩形，WF＝SG＝EH＝DT＝2，从而求得△ABC的周长．
【解答】解：如图．连接AR、RS、RW、DF、DE，由题意知，△ABC是等边三角形，∠EDB＝60°，BD是∠EBF的平分线，
∴∠DBE＝30°，BE＝BF＝DEcot30°＝3，
同理，AW＝AS＝CG＝CH＝3，四边形WFDR，SGTR，THED是矩形，WF＝SG＝EH＝DT＝2，
∴△ABC的周长＝6BE+3EH＝18+6．
故选：B．

【点评】本题考查了切线长定理、等边三角形的判定和性质等知识点．
22．如图，△ABC中，∠C＝90°，AC＝8，BC＝6，O为△ABC的内切圆圆心，则阴影部分的面积为（　　）

A．2π B． C． D．
【分析】先利用勾股定理计算出AB＝10，再利用直角三角形内切圆半径的计算方法得到OD＝2，接着三角形角平分线的性质得到∠AOB＝135°，然后根据扇形面积公式计算得出答案．
【解答】解：如图，

∵∠C＝90°，AC＝8，BC＝6，
∴AB＝＝＝10，
∵⊙O为ABC的内切圆，
∴OD＝＝2，OB平分∠BAC，OC平分∠ABC，
∴∠AOB＝90°+∠C＝90°+×90°＝135°，
∴阴影部分的面积为＝．
故选：C．
【点评】本题考查了三角形的内切圆与内心：三角形的内心到三角形三边的距离相等；三角形的内心与三角形顶点的连线平分这个内角．也考查了直角三角形内切圆半径的计算方法和扇形面积公式．
23．已知如图，△ABC的内切圆⊙O与BC，CA，AB分别相切于点D，E，F，且AB＝9cm，BC＝15cm，CA＝12cm．求AF，BD，CE的长．

【分析】利用切线长定理得到AE＝AF，BF＝BD，CD＝CE，设AF＝xcm，则AE＝xcm，BF＝BD＝（9﹣x）cm，CE＝CD＝（12﹣x）cm，所以9﹣x+12﹣x＝15，解方程求出x，从而得到AF、BD、CE的长．
【解答】解：∵△ABC的内切圆⊙O与BC、CA、AB分别相交于点D、E、F，
∴AE＝AF，BF＝BD，CD＝CE，
设AF＝xcm，则AE＝xcm，BF＝BD＝AB﹣AF＝（9﹣x）cm，
∴CE＝CD＝CA﹣AE＝（12﹣x）cm，
∵BD+CD＝BC，
∴9﹣x+12﹣x＝15，
解得x＝3，
∴AF＝3cm，BD＝6cm，CE＝9cm．
【点评】本题考查了三角形的内切圆与内心：三角形的内心到三角形三边的距离相等；三角形的内心与三角形顶点的连线平分这个内角．也考查了切线长定理．
24．如图，在Rt△ABC中，∠C＝90°，AC＝5，⊙O是△ABC的内切圆，半径为2，则图中阴影部分的面积为（　　）

A．30﹣4π B．30﹣4π C．60﹣16π D．30﹣16π
【分析】先由切线长定理及勾股定理计算出三角形的另外两边长，再根据图中阴影部分面积＝△ABC的面积﹣⊙O的面积计算即可．
【解答】解：如图，记三个切点分别为D、E、F，连接OD、OE、OF，

则∠ODC＝∠OEC＝∠OFA＝90°，OD＝OE＝OF＝2，
∴四边形ODCE是正方形，
∴CE＝CD＝2，
∵⊙O是△ABC的内切圆，
∴AE＝AF＝5﹣2＝3，BD＝BF，
设BD＝BF＝x，则BC＝x+2，AB＝x+3，
在Rt△ABC中，52+（x+2）2＝（x+3）2，
∴x＝10，
∴BC＝12，
∴S阴影＝S△ABC﹣S⊙O＝＝30﹣4π．
故选：A．
【点评】本题考查切线长定理及勾股定理，解题关键是熟练应用切线长定理．
25．如图，木工用角尺的短边紧靠⊙O于点A，长边与⊙O相切于点B，角尺的直角顶点为C．已知AC＝6cm，CB＝8cm，则⊙O的半径为 　 　cm．

【分析】连接OA，OB，过点A作AD⊥OB于点D，利用矩形的判定与性质得到BD＝AC＝6cm，AD＝BC＝8cm，设⊙O的半径为rcm，在Rt△OAD中，利用勾股定理列出方程即可求解．
【解答】解：连接OA，OB，过点A作AD⊥OB于点D，如图，

∵长边与⊙O相切于点B，
∴OB⊥BC，
∵AC⊥BC，AD⊥OB，
∴四边形ACBD为矩形，
∴BD＝AC＝6cm，AD＝BC＝8cm．
设⊙O的半径为rcm，
则OA＝OB＝rcm，
∴OD＝OB﹣BD＝（r﹣6）cm，
在Rt△OAD中，
∵AD2+OD2＝OA2，
∴82+（r﹣6）2＝r2，
解得：r＝．
故答案为：．
【点评】本题主要考查了圆的切线的性质定理，勾股定理，矩形的判定与性质，依据题意添加适当的辅助线是解题的关键．
26．如图，AB为⊙O的直径，点P在AB的延长线上，PC，PD分别与⊙O相切于点C，D，若∠CPA＝40°，则∠CAD的度数为 　 　．

【分析】连接OC，OD，利用切线的性质定理和切线长定理求得∠OCP＝∠ODP＝90°，∠CPD＝80°，利用四边形的内角和定理和圆周角定理解得即可得出结论．
【解答】解：连接OC，OD，如图，

∵PC，PD分别与⊙O相切于点C，D，
∴OC⊥PC，OD⊥PD，∠CPO＝∠DPO＝40°，
∴∠OCP＝∠ODP＝90°，∠CPD＝80°．
∵四边形PCOD的内角和为360°，
∴∠CPD+∠COD＝180°，
∴∠COD＝100°．
∴∠CAD＝∠COD＝50°．
故答案为：50°．
【点评】本题主要考查了圆的切线的性质定理和切线长定理，圆周角定理，四边形的内角和，连接OC，OD是解题的关键．

题型4：切线的判定
27．如图，AB是圆O的一条弦，点E是劣弧AB的中点，直线CD经过点E且与直线AB平行，证明：直线CD是圆O的切线．

【分析】连接OE交AB于点F,由垂径定理得出OE⊥AB,由平行线的性质得出CD⊥OE,则可得出结论．
【解答】证明:连接OE交AB于点F,

∵点E是劣弧AB的中点,
∴OE⊥AB,
∵AB∥CD,
∴CD⊥OE,
∵OE是圆的半径,
∴直线CD是圆O的切线．
【点评】此题主要考查了切线的判定，同时也利用了垂径定理及平行线的性质,熟练掌握切线的判定是解题的关键．
28．如图，CD是⊙O的直径，并且AC＝BC，AD＝BD．求证：直线AB是⊙O的切线．

【分析】欲证明AB是⊙O的切线，只要证明CD⊥AB即可；
【解答】证明：∵CA＝CB，AD＝DB，
∴CD⊥AB，
∵CD是直径，
∴AB是⊙O的切线．
【点评】本题考查切线的判定、等腰三角形的性质等知识，解题的关键是熟练掌握基本知识，属于中考基础题．
29．如图，AB是⊙O的直径，⊙O交BC的中点于D，DE⊥AC于E，连接AD，求证：DE是⊙O的切线．

【分析】连接OD，只要证得∠EDO＝90°即可得到DE是⊙O的切线．
【解答】证明：连接OD，
∵D是BC的中点，
∴BD＝CD．
∵OA＝OB，
∴OD∥AC．
又∵DE⊥AC，
∴OD⊥DE．
∴DE是⊙O的切线．

【点评】本题考查了切线的判定定理：经过半径的外端且垂直于这条半径的直线是圆的切线．在判定一条直线为圆的切线时，当已知条件中未明确指出直线和圆是否有公共点时，常过圆心作该直线的垂线段，证明该线段的长等于半径，可简单的说成“无交点，作垂线段，证半径”；当已知条件中明确指出直线与圆有公共点时，常连接过该公共点的半径，证明该半径垂直于这条直线，可简单地说成“有交点，作半径，证垂直”．也考查了三角形中位线定理．
30．如图，AB为⊙O直径，AB＝AC，BC与⊙O交于D，且DE⊥AC．求证：DE是⊙O切线．

【分析】首先连接AD，DO，进而利用圆周角定理以及等腰三角形的性质和三角形中位线定理求出DO∥AC，进而得出即可．
【解答】证明：连接AD，DO，
∵AB是⊙O的直径，
∴∠ADB＝90°，
∵AB＝AC，
∴BD＝CD，
∵AO＝BO，
∴DO是△ABC的中位线，
∴DO∥AC，
∵DE⊥AC
∴OD⊥DE，
∴DE是⊙O的切线．

【点评】此题主要考查了切线的判定以及圆周角定理以及等腰三角形的性质和三角形中位线定理等知识，得出DO∥AC是解题关键．
31．如图，已知⊙O是四边形ABCD的外接圆，AB是⊙O的直径，BC＝CD，过点C作PM⊥AD交AD的延长线于点M，交AB的延长线于点P．
（1）求证：PM是⊙O的切线；
（2）若AB＝10，AD＝6，求CM的长．

【分析】（1）连接OC，根据弦，弧，圆心角的关系得到∠DAC＝∠CAO，推出AD∥OC，根据平行线的性质得到∠M＝∠OCP，于是得到结论；
（2）连接BD交OC于E，根据垂径定理得到OC⊥BD，根据圆周角定理得到BD⊥AM，推出四边形CMDE是矩形，根据矩形的性质得到CM＝DE，根据勾股定理即可得到结论．
【解答】解：（1）连接OC，
∵BC＝CD，
∴＝，
∴∠DAC＝∠CAO，
∵OC＝OA，
∴∠CAO＝∠ACO，
∴∠DAC＝∠ACO，
∴AD∥OC，
∴∠M＝∠OCP，
∵PM⊥AM，
∴OC⊥PM，
∴PM是⊙O的切线；

（2）连接BD交OC于E，
∵＝，
∴OC⊥BD，
∵AB是⊙O的直径，
∴BD⊥AM，
∴四边形CMDE是矩形，
∴CM＝DE，
∵BD＝＝8，
∴CM＝DE＝BD＝4．

【点评】本题考查了切线的判定，矩形的判定和性质，勾股定理，正确的作出辅助线是解题的关键．
32．如图，AB是⊙O的直径点F、C是半圆弧ABC上的三等分点，连接AC，AF，过点C作CD⊥AF交AF的延长线于点D，垂足为D．
（1）求证：CD是⊙O的切线；
（2）若⊙O的半径为4，求CD的长．

【分析】（1）连接OC，由OA＝OC，利用等边对等角得到一对角相等，再由等弧所对的圆周角相等得到一对角相等，等量代换得到一对内错角相等，确定出OC与AD平行，由CD与AD垂直，得到CD与OC垂直，即可得证；
（2）连接OF，利用等弧所对的圆心角相等及平角定义求出∠OCB的度数，在直角三角形OCE中，求出CE的长，利用角平分线性质得到CD＝CE，即可求出CD的长．
【解答】（1）证明：连接OC，
∵OA＝OC，
∴∠OAC＝∠OCA，
∵＝，
∴∠DAC＝∠CAB，
∴∠OCA＝∠DAC，
∴OC∥AD，
∵CD⊥AD，
∴CD⊥OC，
则CD为圆O的切线；
（2）解：连接OF，过C作CE⊥AB，
∵＝＝，
∴∠AOF＝∠FOC＝∠COB＝60°，
在Rt△OCE中，OC＝4，∠OCE＝30°，
∴CE＝2，
∵AC平分∠DAB，CD⊥AD，CE⊥AB，
∴CD＝CE＝2．

【点评】此题考查了切线的判定，圆心角、弧及弦之间的关系，等腰三角形的性质，平行线的判定与性质，熟练掌握切线的判定方法是解本题的关键．
33．如图，已知AC是⊙O的直径，BC是⊙O的弦，P是⊙O外一点，连接PB，AB，OB，且∠PBA＝∠ACB．
（1）求证：PB是⊙O的切线；
（2）连接OP，若AP＝BP，且OP＝8，⊙O的半径是2，求△OAP的面积．

【分析】（1）欲证明PB是切线，只要证明∠PBO＝90°即可．
（2）先证明△POB≌△POA，推出∠PAO＝∠PBO＝90°，推出PA＝＝＝2，根据S△POA＝•OA•PA计算即可．
【解答】解：（1）证明：∵AC是直径，
∴∠ABC＝90°，
∵OC＝OB，
∴∠OCB＝∠OBC，
∵∠PBA＝∠ACB，
∴∠PBA＝∠OBC，
∵∠OBA+∠OBC＝90°，
∴∠OBA+∠PBA＝90°，
∴∠PBO＝90°，
∴PB⊥OB，
∴PB是⊙O的切线．

（2）在△POB和△POA中，
，
∴△POB≌△POA，
∴∠PAO＝∠PBO＝90°，
∴PA＝＝＝2，
∴S△POA＝•OA•PA＝×2×2＝4．

【点评】本题考查切线的性质、圆周角定理、勾股定理、全等三角形的判定和性质等知识，解题的关键是灵活运用所学知识解决问题，属于基础题中考常考题型．
34．如图已知AB是⊙O的直径，AB＝10，点C，D在⊙O上，DC平分∠ACB，点E在⊙O外，∠EAC＝∠D．
（1）求证：AE是⊙O的切线；
（2）求AD的长．

【分析】（1）根据圆周角定理得出∠BCA＝90°，∠D＝∠B，求出∠B+∠BAC＝90°，∠EAC＝∠B，推出∠EAC+∠BAC＝90°，根据切线的判定得出即可；
（2）连接BD，进而利用勾股定理得出AD的长．
【解答】（1）证明：∵AB是⊙O的直径，
∴∠BCA＝90°，
∴∠B+∠BAC＝90°，
∵∠D＝∠B，∠EAC＝∠D，
∴∠EAC＝∠B，
∴∠EAC+∠BAC＝90°，
∴BA⊥AE，
∵BA过O，
∴直线AE是⊙O的切线；

（2）解：连接BD，
∵∠BCD＝∠DCA，
∴BD＝AD，
∵AB＝10，
∴AD＝BD＝×10＝5．

【点评】本题考查了圆周角定理，切线的判定的应用，能求出BA⊥AE是解此题的关键，注意：经过半径的外端，且垂直于这条半径的直线是圆的切线．
35．如图，AB是⊙O的直径，点D是⊙O上的一点，OC∥AD交⊙O于点E，点F在CD的延长线上，∠BOC+∠ADF＝90°．
（1）求证：CD是⊙O的切线；
（2）若AB＝6，CD＝4，求CE．

【分析】（1）连接OD，由OC∥AD得到∠BOC＝∠A，而∠ODA＝∠A，则∠ODA＝∠BOC，由于∠BOC+∠ADF＝90°，所以∠ODA+∠ADF＝90°，然后根据切线的判定定理得到结论；
（2）延长CO交⊙O于H，于是得到EH＝AB＝6，根据切割线定理即可得到结论．
【解答】（1）证明：连接OD，如图，
∵OC∥AD，
∴∠BOC＝∠A，
而OD＝OA，
∴∠ODA＝∠A，
∴∠ODA＝∠BOC，
∵∠BOC+∠ADF＝90°，
∴∠ODA+∠ADF＝90°，
即∠ODF＝90°，
∴OD⊥DF，
∴CD是⊙O的切线；

（2）延长CO交⊙O于H，
∴EH＝AB＝6，
∵CD是⊙O的切线，
∴CD2＝CE•CH，
即42＝CE（CE+6），
∴CE＝2（负值舍去）．

【点评】本题考查了切线的判定定理，切割线定理，知道经过半径的外端且垂直于这条半径的直线是圆的切线是解题的关键．

题型5：辅助圆-定点定圆（提升）
36．如图，在平面直角坐标系中，点A、B的坐标分别为（﹣3，0）、（0，4），以点A为圆心，以AB长为半径画弧交x轴上点C，则点C的坐标为（　　）

A．（5，0） B．（2，0）
C．（﹣8，0） D．（2，0）或（﹣8，0）
【分析】根据题意求出AB的长，以A为圆心作圆，与x轴交于C，C′，求出C的坐标即可．
【解答】解：∵点A、B的坐标分别为（﹣3，0）、（0，4），
∴OA＝3，OB＝4，
∴AB＝＝5，
∴AC′＝5，AC＝5，
∴C′点坐标为（2，0）；C点坐标为（﹣8，0）．
故选：D．

【点评】本题考查了勾股定理、坐标与图形的性质，作出辅助圆是解题的关键．
37．如图，点A，B的坐标分别为A（4，0），B（0，4），C为坐标平面内一点，BC＝2，点M为线段AC的中点，连接OM，OM的最大值为 　 　．

【分析】先判断出点C的运动轨迹是在半径为2的⊙B上，再取OD＝OA＝4，连接OD，则OM是△ACD的中位线，OM＝，进而可得OM最大值时，CD取最大值，此时D、B、C三点共线，计算即可求出结果．
【解答】解：∵C为坐标平面内一点，BC＝2，
∴点C的运动轨迹是在半径为2的⊙B上，
如图，取OD＝OA＝4，连接OD，

∵点M为线段AC的中点，
∴OM是△ACD的中位线，
∴OM＝，
∴OM最大值时，CD取最大值，此时D、B、C三点共线，
此时在Rt△OBD中，BD＝＝4，
∴CD＝2+4，
∴OM的最大值是1+2．
故答案为：1+2．
【点评】本题考察了坐标和三角形的中位线，定点定长构造辅助圆等，解题关键是确定点C的运动轨迹．
38．如图，四边形ABCD中，AB＝AC＝AD，∠CBD＝20°，∠BDC＝30°，则∠BAD＝　 　．

【分析】先根据AB＝AC＝AD可知，B、C、D三点在以点A为圆心，以AB为半径的圆上，再根据圆周角定理即可得出结论．
【解答】解：∵AB＝AC＝AD，
∴B、C、D三点在以点A为圆心，以AB为半径的圆上，
∵∠CBD＝20°，∠BDC＝30°，
∴∠BAC＝2∠BDC＝60°，∠CAD＝2∠CBD＝40°，
∴∠BAD＝∠BAC+∠CAD＝60°+40°＝100°．
故答案为：100°．
【点评】本题考查的是圆周角定理，熟知在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半是解答此题的关键．
39．如图，在矩形ABCD中，已知AB＝3，BC＝4，点P是BC边上一动点（点P不与B，C重合），连接AP，作点B关于直线AP的对称点M，则线段MC的最小值为（　　）

A．2 B． C．3 D．
【分析】当A，M，C三点共线时，线段CM的长度最小，求出此时CM的长度即可．
【解答】解：连接AM，

∵点B和M关于AP对称，
∴AB＝AM＝3，
∴M在以A圆心，3为半径的圆上，
∴当A，M，C三点共线时，CM最短，
∵AC＝，AM＝AB＝3，
∴CM＝5﹣3＝2，
故选：A．
【点评】本题主要考查圆的性质，关键是要考虑到点M在以A为圆心，3为半径的圆上．

41．在四边形ABCD中，DC∥AB，BC＝1，AB＝AC＝AD＝2，则BD长为多少　　．

【分析】以A为圆心，AB长为半径作圆，延长BA交⊙A于F，连接DF．在△BDF中，由勾股定理即可求出BD的长．
【解答】解：以A为圆心，AB长为半径作圆，延长BA交⊙A于F，连接DF．
∵AB＝AC＝AD＝2，
∴D，C在圆A上，
∵DC∥AB，
∴弧DF＝弧BC，
∴DF＝CB＝1，BF＝AB+AF＝2AB＝4，
∵FB是⊙A的直径，
∴∠FDB＝90°，
∴BD＝＝
故答案为：．

【点评】本题考查了勾股定理，解题的关键是作出以A为圆心，AB长为半径的圆，构建直角三角形，从而求解．

题型6：辅助圆-定弦定角（提升）
42．如图，在矩形ABCD中，AB＝8，BC＝6，点P在矩形的内部，连接PA，PB，PC，若∠PBC＝∠PAB，则PC的最小值是（　　）

A．6 B．﹣3 C．2﹣4 D．4﹣4
【分析】首先证明∠PAB+∠PBA＝90°，得∠APB＝90°，则点P在以AB为直径的圆上运动，设圆心为O，连接OC交⊙O于P，此时PC最小，利用勾股定理求出OC的长即可．
【解答】解：∵四边形ABCD是矩形，
∴∠ABC＝90°，
∴∠ABP+∠PBC＝90°，
∵∠PBC＝∠PAB，
∴∠PAB+∠PBA＝90°，
∴∠APB＝90°，
∴点P在以AB为直径的圆上运动，设圆心为O，连接OC交⊙O于P，此时PC最小，

∵OC＝＝＝2，
∴PC的最小值为2﹣4，
故选：C．
【点评】本题主要考查了矩形的性质，勾股定理等知识，利用定边对定角确定点P的运动路径是解题的关键．
43．如图，△ABC中，∠C＝90°，∠BAC＝30°，AB＝2，点P从C点出发，沿CB运动到点B停止，过点B作射线AP的垂线，垂足为Q，点Q运动的路径长为（　　）

A． B． C． D．
【分析】由AQ⊥BQ，得点Q在以AB为直径的⊙O上运动，运动路径为，连接OC，代入弧长公式即可．
【解答】解：∵AQ⊥BQ，
∴点Q在以AB为直径的⊙O上运动，运动路径为，连接OC，

∵∠ACB＝90°，OA＝OB，
∴CO＝OA＝1，
∴∠COB＝2∠CAB＝60°，
∴的长为，
故选：D．
【点评】本题主要考查了圆周角定理，弧长公式，确定点Q在以AB为直径的⊙O上运动是解题的关键．
44．如图，在矩形ABCD中，AD＝5，AB＝3，点E在AB上，＝，在矩形内找一点P，使得∠BPE＝60°，则线段PD的最小值为（　　）

A．2﹣2 B． C．4 D．2
【分析】如图，在BE的上方，作△OEB，使得OE＝OB，∠EOB＝120°，连接OD，过点O作OQ⊥BE于Q，OJ⊥AD于J．证明点P的运动轨迹是以O为圆心，OE为半径的⊙O，推出当点P落在线段OD上时，DP的值最小，想办法求出OD，OP，可得结论．
【解答】解：如图，在BE的上方，作△OEB，使得OE＝OB，∠EOB＝120°，连接OD，过点O作OQ⊥BE于Q，OJ⊥AD于J．

∵∠BPE＝∠EOB，
∴点P的运动轨迹是以O为圆心，OE为半径的⊙O，
∴当点P落在线段OD上时，DP的值最小，
∵四边形ABCD是矩形，
∴∠A＝90°，
∵AB＝3，AE：EB＝1：2，
∴BE＝2，
∵OE＝OB，∠EOB＝120°，OQ⊥EB，
∴EQ＝BQ＝，∠EOQ＝∠BOQ＝60°，
∴OQ＝1，OE＝2，
∵OJ⊥AD，OQ⊥AB，
∴∠A＝∠AJO＝∠AQO＝90°，
∴四边形AQOJ是矩形，
∴AJ＝OQ＝1，
JO＝AQ＝2，
∵AD＝5，
∴DJ＝AD﹣AJ＝4，
∴OD＝＝＝2，
∴PD的最小值＝OD﹣OP＝2﹣2，
故选：A．
【点评】本题考查点与圆的位置关系，矩形的性质，圆周角定理，解直角三角形等知识，解题的关键是学会添加辅助圆解决问题，属于中考选择题中的压轴题．
45．如图，点A是半径为8的圆O上一定点，点B是圆O上一动点，点P是弦AB的中点，则点B绕圆周运动一周，点P所经过的路径长为（　　）

A．4 B．8 C．4π D．8π
【分析】连接OP，OA，由点P为AB的中点，得∠OPA＝90°，则点P在以OA为直径的圆上运动，求出圆周长即可．
【解答】解：连接OP，OA，

∵点P为AB的中点，
∴∠OPA＝90°，
∴点P在以OA为直径的圆上运动，
∵OA＝8，
∴点P的运动路径长为：2π×4＝8π，
故选：D．
【点评】本题主要考查了垂径定理，利用定弦对定角确定点P的运动路径是解题的关键．
46．如图，P是矩形ABCD内一点，AB＝4，AD＝2，AP⊥BP，则当线段DP最短时，CP＝　 　．

【分析】因为AP⊥BP，则P点在AB为直径的半圆上，当P点为AB的中点O与D点连线与半圆AB的交点时，DP最短，求出此时PC的长度便可．
【解答】解：以AB为直径作半圆O，连接OD，与半圆O交于点P′，当点P与P′重合时，DP最短，

AO＝OP′＝OB＝AB＝2，
∵AD＝2，∠BAD＝90°，
∴OD＝2，∠ADO＝∠AOD＝∠ODC＝45°，
∴DP′＝OD﹣OP′＝2﹣2，
过P′作P′E⊥CD于点E，则
P′E＝DE＝DP′＝2﹣，
∴CE＝CD﹣DE＝+2，
∴CP′＝．
故答案为：2．
【点评】本题是一个矩形的综合题，主要考查了矩形的性质，勾股定理，圆的性质，关键是作辅助圆和构造直角三角形．

题型7：辅助圆-对角互补（提升）
47．如图，在四边形ABCD中，∠BAD＝∠BCD＝90°，∠ACD＝30°，AD＝2，E是AC的中点，连接DE，则线段DE长度的最小值为 　 ．

【分析】先判断出A、B、C、D四点共圆，且圆心为BD中点，再连接AO、CO，取AO中点F，连接EF，DF，利用圆周角定理及等边三角形的判定可得到△OAD为等边三角形，进而得到半径长、DF、EF，最后利用三角形三边关系即可求出DE最小值．
【解答】解：∵∠BAD＝∠BCD＝90°，
∴A、B、C、D四点共圆，且BD为直径，取BD中点O，则圆心为点O，
连接AO、CO，取AO中点F，连接EF，DF，
∵∠ACD＝30°，
∴∠AOD＝60°，
∵OA＝OD，
∴△OAD为等边三角形，
∴OA＝OD＝OC＝AD＝2，
∴∠AFD＝90°，则DF＝，
∵EF是△AOC的中位线，
∴EF＝OC＝1，
在△DEF中，DF﹣EF≤DE，
∴当D、E、F三点共线时，DE取到最小，最小值为．

∴DE的最小值为．
【点评】本题考查圆的隐形圆综合题，涉及到圆周角定理，中位线，等边三角形，直角三角形的性质，勾股定理，对角互补构造隐形圆，其中构造圆是解题的关键．
48．已知：在△ABC中，AB＝AC＝6，∠B＝30°，E为BC上一点，BE＝2EC，DE＝DC，∠ADC＝60°，则AD的长 　 　．

【分析】连接AE，根据等腰三角形的性质及勾股定理得到AE＝CE，证明A、D、C、E四点共圆，根据同弧所对圆周角相等，得到∠ADE＝30°．过A点作AM⊥DE，易得△AME是等腰直角三角形，从而求出AM长度，在Rt△AMD中，根据30°直角三角形的性质可求AD长度．
【解答】解：连接AE，过点A作AH⊥BC于H点，在Rt△ABH中，
∵∠B＝30°，∴AH＝AB＝3．
利用勾股定理可得BH＝3，
根据等腰三角形性质可知CH＝BH＝3，BC＝6．
∴CE＝BC＝2．
∴HE＝CH﹣CE＝．
在Rt△AHE中，由勾股定理可求AE＝2．
所以AE＝CE，∠CAE＝∠ACB＝30°，
所以∠AEB＝60°＝∠ADC，
∴四边形AECD对角互补，
∴点A、D、C、E四点共圆，
∴∠ADE＝∠ACE＝30°，
所以∠CDE＝∠ADC﹣∠ADE＝30°．
∵DE＝DC，∴∠DEC＝75°．
∴∠AED＝120°﹣75°＝45°．
过点A作AM⊥DE于M点，
则AM＝AE＝．
在Rt△AMD中，∠ADM＝30°，
∴AD＝2AM＝．
故答案为2．

【点评】本题主要考查了等腰三角形的性质、含30度角的直角三角形的性质、勾股定理以及圆周角的性质，正确作出辅助线、辅助圆是解题的关键．
49．如图，矩形ABCD的对角线相交于O，过点O作OE⊥BD，交AD点E，连接BE，若∠ABE＝20°，则∠AOE的大小是（　　）

A．10° B．15° C．20° D．30°
【分析】如图取BE的中点K．连接AK、OK．只要证明KA＝KB＝KO＝KE，推出A、B、O、E四点共圆，可得∠ABE＝∠AOE＝20°．
【解答】解：如图取BE的中点K．连接AK、OK．

∵四边形ABCD是矩形，
∴∠BAE＝90°，
∵EO⊥BD，
∴∠BOE＝90°，
∴四边形ABOE对角互补，
∴A、B、O、E四点共圆，
∵BK＝KE，
∴KA＝KB＝KO＝KE，
∴∠ABE＝∠AOE＝20°，
故选：C．
【点评】本题考查矩形的性质、直角三角形斜边中线定理、四点共圆等知识，解题的关键是学会添加常用辅助线，利用辅助圆解决问题，属于中考常考题型．
50．如图所示，∠MON＝45°，Rt△ABC，∠ACB＝90°，BC＝6，AC＝8，当A、B分别在射线OM、ON上滑动时，OC的最大值为（　　）

A．12 B．14 C．16 D．14
【分析】在AB的下方作等腰直角△AQB，∠AQB＝90°，作BH⊥QC于H，勾股定理得AB＝，点O在以点Q为圆心，QB为半径的圆上，当点C、Q、O共线时，OC最大，再求出CQ的长即可．
【解答】解：如图，在Rt△ABC中，由勾股定理得AB＝，
在AB的下方作等腰直角△AQB，∠AQB＝90°，作BH⊥QC于H，

∴点O在以点Q为圆心，QB为半径的圆上，
∵∠AQB+∠ACB＝180°，
∴点A、C、B、Q共圆，
∴∠BCQ＝∠BAQ＝45°，
∴BH＝CH＝3，
在Rt△BQH中，由勾股定理得QH＝4，
∴CQ＝7，
当点C、Q、O共线时，OC最大，
∴OC的最大值为OQ+CQ＝5+7＝12，
故选：A．
【点评】本题主要考查了勾股定理，等腰直角三角形的性质，定边对定角确定点O的运动路径，以及对角互补模型是解题的关键，难度较大．