初中数学24.2.2 直线和圆的位置关系达标测试
展开
24.2.2 切线的判定与性质及切线长定理
|
注意：切线的判定方法： （1）定义：直线和圆有唯一公共点时，这条直线就是圆的切线； （2）定理：和圆心的距离等于半径的直线是圆的切线； （3）判定定理：经过半径外端并且垂直于这条半径的直线是圆的切线.（切线的判定定理中强调两点：一是直线与圆有一个交点，二是直线与过交点的半径垂直，缺一不可）. |
题型1：切线的判定-连半径证垂直
|
【变式1-1】如图，在⊙O中，AB为直径，BP为⊙O的弦，AC与BP的延长线交于点C，且
|
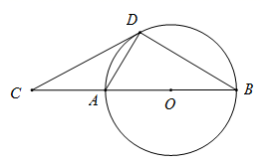
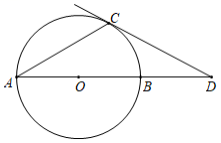
【变式1-2】如图，D为⊙O上一点，点C在直径BA的延长线上，且
|
题型2：切线的判定-作垂直证半径
求证：AC是
|
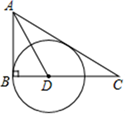
【变式2-1】如图，在Rt△ABC中，∠ABC=90°，∠BAC的平分线交BC于D，以D为圆心，DB长为半径作⊙D．求证：AC与⊙D相切.
|
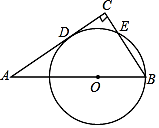
【变式2-2】如图，点C在以AB为直径的⊙O上，弧AC＝
|
题型3：切线的判定多选项问题
A．与圆只有一个交点的直线是圆的切线 B．经过半径的外端，且垂直于这条半径的直线是圆的切线 C．与圆心的距离等于这个圆的半径的直线是圆的切线 D．垂直于半径的直线是圆的切线
|
【变式3-1】下列命题中：①相等的圆心角所对的弧相等；②平分弦的直径垂直于弦；③垂直于半径的直线是圆的切线；④E，F是∠AOB的两边OA，OB上的两点，则不同的E，O，F三点确定一个圆：其中正确的有（ ） A．1个 B．2个 C．3个 D．0个
|
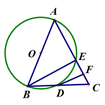
【变式3-2】如图，AB为⊙O的直径，AB＝AC，AC交⊙O于点E，BC交⊙O于点D，F为CE的中点，连接DF.给出以下五个结论：①BD＝DC；②AD＝2DF；③
A．4 B．3 C．2 D．1
|
切线的性质定理： |
注意：切线的性质： （1）切线和圆只有一个公共点；（2）切线和圆心的距离等于圆的半径； （3）切线垂直于过切点的半径；（4）经过圆心垂直于切线的直线必过切点； （5）经过切点垂直于切线的直线必过圆心. |
题型4：切线的性质-求长度
A．8 B．
|
【变式4-1】如图，
A．6 B．4 C．
|
【变式4-2】如图，Rt△ABC中，∠C=90°，BC=3，点O在AB上，OB=2，以OB为半径的⊙O与AC相切于点D，交BC于点E，求弦BE的长．
|
题型5：切线的性质-求角度
A．35° B．40° C．45° D．50°
|
【变式5-1】如图，已知
|
【变式5-2】如图，AB是
|
题型6：切线的性质-求半径
|
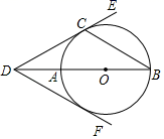
【变式6-1】如图，BE是⊙O的直径，点A和点D是⊙O上的两点，过点A作⊙O的切线交BE延长线于点C．
（1）若∠ADE＝28°，求∠C的度数； （2）若AC＝2
|
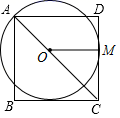
【变式6-2】如图，O为正方形ABCD对角线上一点，以O为圆心，OA的长为半径的⊙O与CD相切于点M，
（1）求证：BC与⊙O相切； （2）若正方形的边长为1，求⊙O的半径.
|
切线长定理 圆外切四边形的性质：圆外切四边形的两组对边之和相等. |
注意： |
题型7：切线长定理-求周长
A．8cm B．5cm C．6.5cm D．无法确定
|
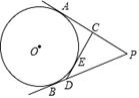
【变式7-1】如图，PA、PB分别切⊙O于点A、B，且PA＝8，CD切⊙O于点E，交PA、PB于C、D两点，则△PCD的周长为（ ）
A．32 B．24 C．16 D．8
|
【变式7-2】如图，△ABC中，∠C＝90°，BC＝5，⊙O与△ABC的三边相切于点D、E、F，若⊙O的半径为2，则△ABC的周长为（ ）
A．14 B．20 C．24 D．30
|
三角形的内切圆：与三角形各边都相切的圆叫做三角形的内切圆. |
注意： |
题型8：三角形的内切圆-求半径
A．1 B．
|
【变式8-1】如图，Rt△ABC中，∠C＝90°，AB＝13，BC＝5，则其内切圆半径为（ ）
A．1 B．2 C．3 D．4
|
【变式8-2】若方程x2-7x+12=0的两个根分别是直角三角形两直角边的长，则这个直角三角形的内切圆半径为 .
|
题型9：三角形的内切圆-求面积
|
【变式9-1】一直角三角形的斜边长为c，其内切圆半径是r，则三角形面积与其内切圆的面积之比是（ ） A．
|
【变式9-2】正三角形外接圆面积是 A．
|
题型10：三角形的内切圆-求角度
A．
|
【变式10-1】如图，点I是△ABC的内心，点O是△ABC的外心，若∠BOA=140°，则∠BIA的度数是（ ）
A．100° B．120° C．125° D．135°
|
【变式10-2】如图，
A．
|
一、单选题
1．已知⊙O的半径为4，点O到直线m的距离为d，若直线m与⊙O公共点的个数为2个，则d可取（ ）
A．5 B．4.5 C．4 D．0
2．在△ABC中，∠C=90°，AC=6，BC=8，以C 为圆心r为半径画⊙C，使⊙C与线段AB有且只有两个公共点，则r的取值范围是（ ）
A．6≤r≤8 B．6≤r＜8 C．
＜r≤6 D．＜r≤8
3．如图所示，AB是⊙O的直径，点C为⊙O外一点，CA，CD是⊙O的切线，A，D为切点，连接BD，AD．若∠ACD=30°，则∠DBA的大小是（ ）
A．15° B．30° C．60° D．75°
4．在平面直角坐标系中，以点(-1，2)为圆心，1为半径的圆必与( )
A．x轴相交 B．y轴相交 C．x轴相切 D．y轴相切
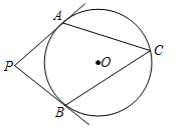
5．如图，过⊙O外一点P引⊙O的两条切线PA、PB，切点分别是A、B，OP交⊙O于点C，点D是 
上不与点A、点C重合的一个动点，连接AD、CD，若∠APB=80°，则∠ADC的度数是（ ）
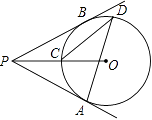
A．15° B．20° C．25° D．30°
6．已知Rt△ACB，∠ACB=90°，I为内心，CI交AB于D，BD=
，AD=
，则S△ACB=（ ）
A．12 B．6 C．3 D．7.5
7．如图，PA、PB是⊙O的切线，切点分别为A、B，点C在⊙O上，如果∠P＝50°，那么∠ACB等于（ ）
A．40° B．50° C．65° D．130°
二、填空题
8．已知在直角坐标平面内，以点P（﹣3，4）为圆心，r为半径画圆，⊙P与坐标轴恰好有三个交点，那么r的取值是 ．
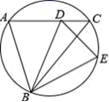
9．如图，△ABC内接于圆，点D是AC上一点，将∠A沿BD翻折，点A正好落在圆上点E处.若∠C=50°，则∠ABE的度数为 .
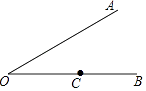
10．如图，∠O=30°，C为OB上一点，且OC=6，以点C为圆心，半径为2 
的圆与直线OA的位置关系是 ．
11．如图，AB为⊙O的直径，C为⊙O外一点，过C作⊙O的切线，切点为B，连接AC交⊙O于点D，∠C＝42°．点E在AB右侧的半圆周上运动（不与A，B重合），则∠AED的度数为 ．
三、解答题
12．在△ABC中， 
，以边AB上一点O为圆心，OA为半径的圈与BC相切于点D，分别交AB，AC于点E，F
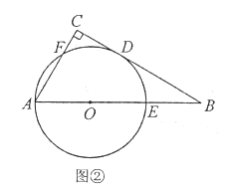
（1）如图①，连接AD，若 
，求∠B的大小；
（2）如图②，若点F为 
的中点， 
的半径为2，求AB的长．
13．已知PA、PB、DE是⊙O的切线，切点分别为A、B、F，PO=13cm，⊙O的半径为5cm，求△PDE的周长．
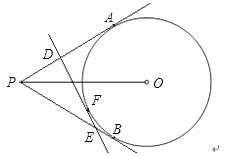
14．如图，已知AB为⊙O的直径，AD，BD是⊙O的弦，BC是⊙O的切线，切点为B，OC∥AD，BA，CD的延长线相交于点E.
（1）求证：DC是⊙O的切线；
（2）若AE＝1，ED＝3，求⊙O的半径．
15．如图，在△ABC中，AB=AC，点D在BC上，BD=DC，过点D作DE⊥AC，垂足为E，⊙O经过A，B，D三点．
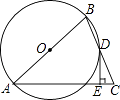
（1）求证：AB是⊙O的直径；
（2）判断DE与⊙O的位置关系，并加以证明；
（3）若⊙O的半径为3，∠BAC=60°，求DE的长．
人教版九年级上册24.2.2 直线和圆的位置关系课堂检测： 这是一份人教版九年级上册24.2.2 直线和圆的位置关系课堂检测，文件包含九年级数学上册242点直线圆与圆的位置关系9大题型-重要笔记2022-2023学年九年级数学上册重要考点精讲精练人教版原卷版docx、九年级数学上册242点直线圆与圆的位置关系9大题型-重要笔记2022-2023学年九年级数学上册重要考点精讲精练人教版解析版docx等2份试卷配套教学资源，其中试卷共33页， 欢迎下载使用。
初中数学人教版九年级上册24.4 弧长及扇形的面积课堂检测： 这是一份初中数学人教版九年级上册24.4 弧长及扇形的面积课堂检测，文件包含九年级数学上册244弧长和扇形面积13大题型-重要笔记2022-2023学年九年级数学上册重要考点精讲精练人教版原卷版docx、九年级数学上册244弧长和扇形面积13大题型-重要笔记2022-2023学年九年级数学上册重要考点精讲精练人教版解析版docx等2份试卷配套教学资源，其中试卷共56页， 欢迎下载使用。
初中数学人教版九年级上册22.1.1 二次函数课后作业题： 这是一份初中数学人教版九年级上册22.1.1 二次函数课后作业题，文件包含九年级数学上册2211二次函数讲+练-重要笔记2022-2023学年九年级数学上册重要考点精讲精练人教版原卷版docx、九年级数学上册2211二次函数讲+练-重要笔记2022-2023学年九年级数学上册重要考点精讲精练人教版解析版docx等2份试卷配套教学资源，其中试卷共18页， 欢迎下载使用。
