三角形和四边形中的中点问题课件 -中考数学复习微专题

这是一份三角形和四边形中的中点问题课件 -中考数学复习微专题，共15页。PPT课件主要包含了练一练，联想二构造中线，＜AD＜4，综合提升等内容，欢迎下载使用。

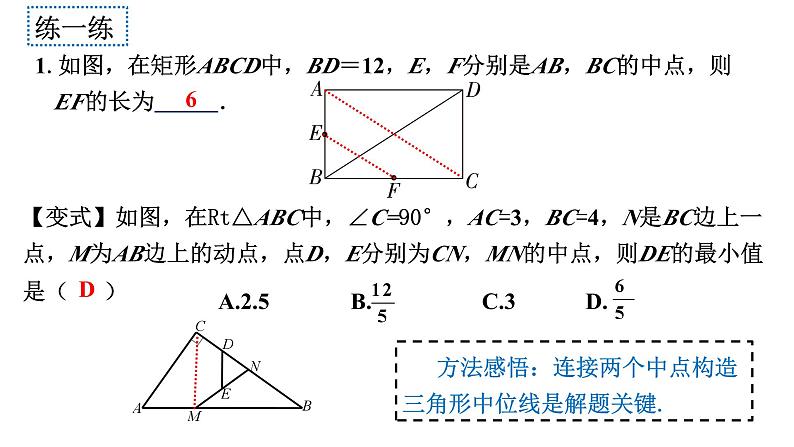
1.如图，在矩形ABCD中，BD＝12，E，F分别是AB，BC的中点，则 EF的长为 ．
方法感悟：连接两个中点构造三角形中位线是解题关键.
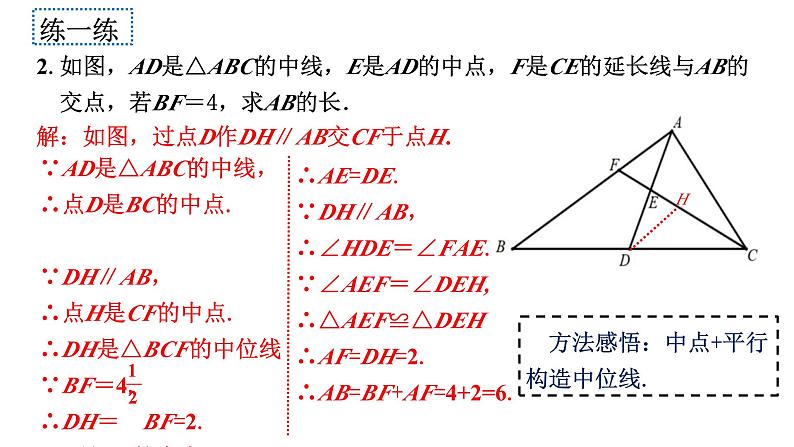
2.如图，AD是△ABC的中线，E是AD的中点，F是CE的延长线与AB的 交点，若BF＝4，求AB的长．
方法感悟：中点+平行 构造中位线.
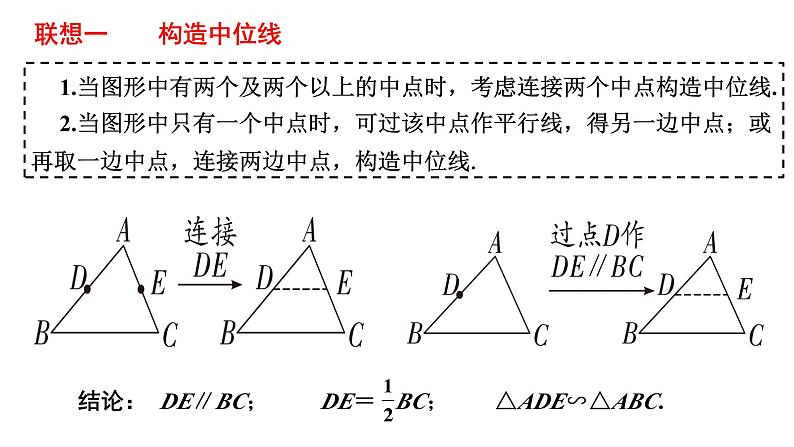
联想一　 构造中位线
1.当图形中有两个及两个以上的中点时，考虑连接两个中点构造中位线. 2.当图形中只有一个中点时，可过该中点作平行线，得另一边中点；或再取一边中点，连接两边中点，构造中位线.
3.如图，在等腰三角形ABC中，AB＝AC＝10，BC＝12，点D为BC的中 点，DE⊥AB于点E，求cs∠BDE的值．
方法感悟：等腰三角形+底边中点联想等腰三角形的“三线合一”.
方法感悟：直角三角形+斜边中点联想“斜边上的中线等于斜边的的一半”.
结论：AD⊥BC；∠BAD＝∠CAD.
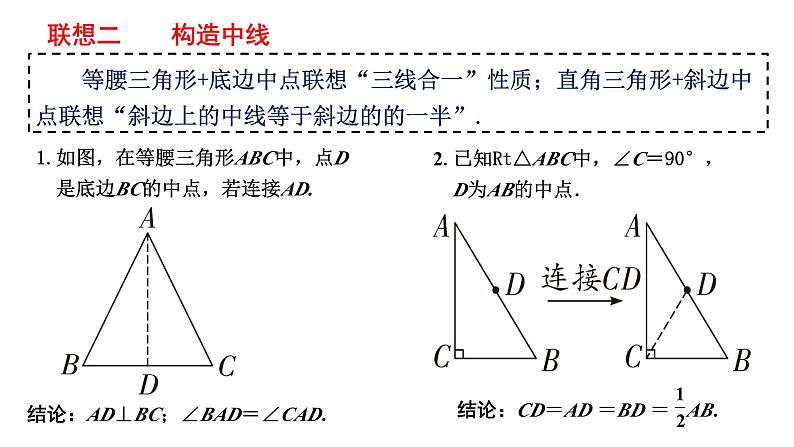
等腰三角形+底边中点联想“三线合一”性质；直角三角形+斜边中点联想“斜边上的中线等于斜边的的一半”.
1.如图，在等腰三角形ABC中，点D 是底边BC的中点，若连接AD.
2.已知Rt△ABC中，∠C＝90°， D为AB的中点．
5. 如图，已知D为△ABC中BC边的中点，AB=12，AC=18，BM⊥AM 于点M.连接DM，若AM为∠BAC的平分线，求MD的长.
联想三 遇见过中点的垂线，考虑用垂直平分线的性质.　
如图，在△ABC中，D是BC的中点，ED⊥BC.结论：BD ＝CD； BE＝CE； ∠BED＝∠DEC；∠EBC＝∠ECB.
6.如图，在△ABC中，D，E分别是BC，AD的中点，若S△AEC= 2cm2， 则S△ABC为（ ） A.4cm2 B.8cm2 C.12cm2 D.16cm2
联想四 遇一边的中点求面积问题，常联想到“三角形的中线等分面积”.
7. 如图，在△ABC中，AB=5，AC=3，AD是BC边上的中线，则AD的取 值范围是　　　　　　. 
方法感悟：将中线延长一倍，构造全等三角形，能将问题轻松解决.
8.如图,在□ABCD中，E为AD的中点，连接CE，以CE为边作正方形 CEFG，使点F落在AB上，FG交BC于点H，求∠ECD的度数.
联想五 遇到三角形一边上的中点，常联想到倍长中线或倍长类中线，构造全等三角形.
结论：△ACD ≌△EBD
结论：△BDE≌△CDF
1.如图，已知四边形ABCD为平行四边形，E为AB边的中点，请仅用无 刻度直尺在下图中按要求作图.(保留作图痕迹). （1）在图①中作出CD边的中点F； （2）在图②中作出AD边的中点G.
解（1）如图①，点F即为所作.
解（2）如图②，点G即为所作.