相似三角形的基本模型-数学中考复习课件PPT

这是一份相似三角形的基本模型-数学中考复习课件PPT，共60页。PPT课件主要包含了基本模型，模型解读，模型应用，变式训练，模型巩固，思路呈现，AE1，△AEF∽△CBF，△AEF≌△DEG，AFDG等内容，欢迎下载使用。

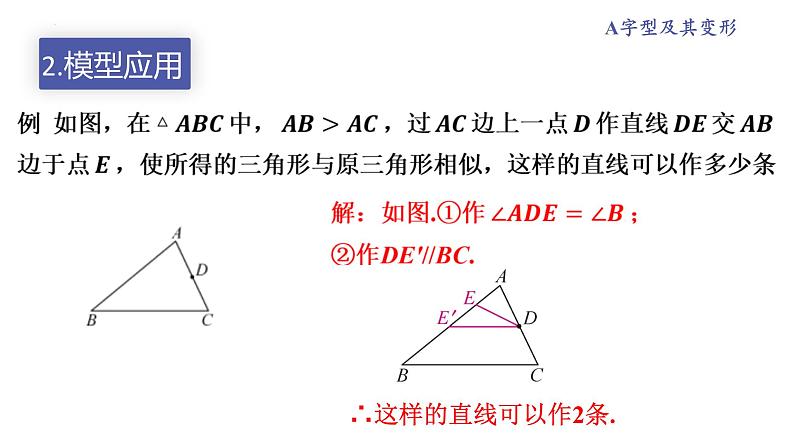
∴这样的直线可以作2条.
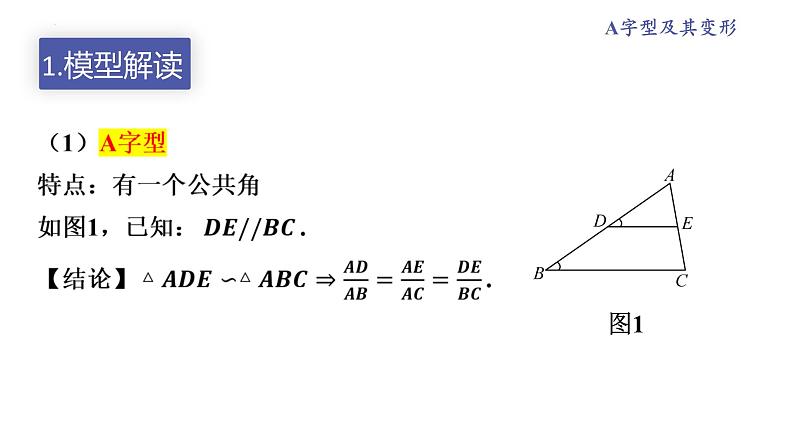
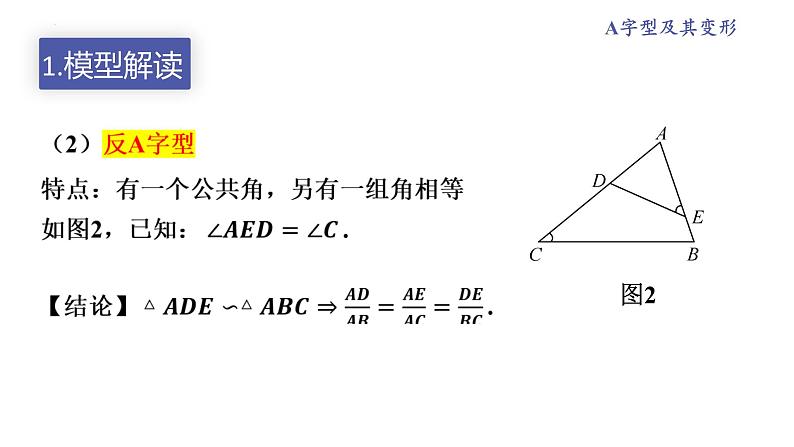
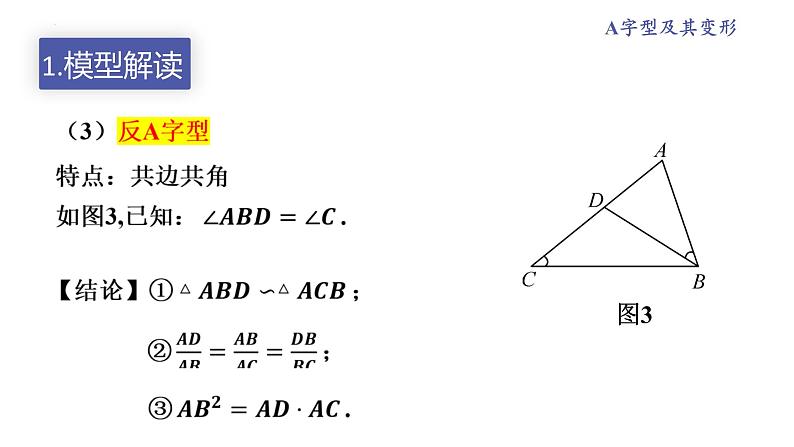
A字型相似与反A字型相似
特征:有一组隐含的等角（即对顶角相等）.
在Rt△ABC中，由勾股定理得BC=4
过点D作DG∥AB交CF于点G
特征：两个相似三角形且共用一组相等角的顶点.
如图，△ABC和△EDC都是等腰三角形，AB＝AC，EC＝ED，∠BAC＝∠CED＝70°，连接EA并延长，交BD于点F，求∠AFB的度数.
∵∠ACB＝∠ECD，∴∠BCD＝∠ACE，∴△BCD∽△ACE，∴∠CBD＝∠CAE，∠BDC＝∠AEC，∴∠AFB＝∠BDC＋∠CDE＋∠DEF＝ ∠CDE＋∠CED＝180°－∠ECD＝180°－55°＝125°.
特征：两个三角形的一条边在一条直线上，并且有一个顶点重合.
设AB=x，则PC=x-4
1. 如图，在等腰△ABC中，AB＝AC＝3，BC＝4，点D是BC的中点，作∠EDF＝∠B，交AC于点E，交BA的延长线于点F，若CE＝1，则AF的长为________．
2. (2022达州改编)如图，点E在矩形ABCD的AB边上，将△ADE沿DE翻折，点A恰好落在BC边上的点F处，若CD＝3BF，BE＝4，则AD的长为________．
3. 如图，在正方形ABCD中，AB＝6，点E是BC边上一点，连接AE，过点E作EF⊥AE交AD的延长线于点F，若AF＝15，则BE的长为________．
4.（1）如图1，在四边形ABCD中，点P为AB上一点，∠DPC = ∠A = ∠B = 90°，找出图中的相似三角形，并说明理由.
解：（1）△ADP ∽ △BPC.理由如下：∵∠DPC = ∠A = ∠B = 90°，∴∠ADP + ∠APD = 90°，∠BPC + ∠APD = 90°.∴∠ADP = ∠BPC.∴△ADP ∽ △BPC .
（2）如图2，在四边形ABCD中，点P为AB上一点，当∠DPC = ∠A = ∠B = α时，（1）中结论是否还成立？说明理由.
解：（2）成立.理由如下：∵∠BPD = ∠DPC + ∠BPC，∠BPD = ∠A + ∠ADP，∴∠DPC + ∠BPC = ∠A + ∠ADP.∵∠DPC = ∠A = ∠B = α，∴∠ADP = ∠BPC.∴△ADP ∽ △BPC .
（3）如图3，在△ABD中，AB = 6，AD = BD = 5，点P以每秒1个单位长度的速度，由点A出发，沿边AB向B运动，且满足∠DPC = ∠A，设点P的运动时间为t秒，当DC = 4BC时，求t的值.
过点P作PM⊥AB于点M过点P作PN⊥BC于点N
含90°的“对角互补”相似型
1.如图，∠AOB = 90°，OC 为∠AOB 内部的一条射线且∠BOC = 60°.点D为射线OA上一点，作CE⊥CD交OB于点E.若CE = 3，则CD = ____.
2. 如图，在Rt△ABC中，∠ABC = 90°，AB = 3，BC = 4，在 Rt△MPN 中，点P在AC上，PM交AB于点 E，PN交 BC于点F.当 PE = 2PF 时，则AP = ____．
3.综合与实践问题情境：如图1，在正方形ABCD中，点E是对角线AC上一点，连接 BE，过点E分别作AC，BE 的垂线，分别交直线BC，CD于点F，G. 试猜想线段BF和GC的数量关系，并说明理由．
数学思考：（1）请回答上述问题.
解：BF = CG.理由如下：∵四边形 ABCD 是正方形 ∴∠ABC = ∠D = 90°AB = CB = CD = AD ∴∠BAC = ∠ACB = 45°∠ACD = ∠DAC = 45°∵EF⊥AC， ∴∠FEC = 90° ∴∠EFB = 90°-∠ACF = 45°∴∠EFB = ∠ECF = ∠ECG ∴EF = EC∵BE⊥EG∴∠BEG = 90°
∴∠BEG = ∠FEC ∴∠BEC + ∠CEG = ∠BEC + ∠FEB ∴∠FEB = ∠CEG ∴△BEF ≌ △GEC∴BF = CG
解：∵四边形ABCD是矩形，∴∠BCD = 90°. ∴∠BCE + ∠ACD = 90°. ∵EF⊥AC，∴∠FEC = 90°. ∴∠BCE + ∠EFB = 90°，∠FEB + ∠BEC = 90°. ∴∠EFB = ∠ECG.
问题拓展：（3）在（2）的条件下，当点E为AC的中点时，请直接写出△CEG的面积.
过点F作FM⊥AB于点M过点G作GN⊥AD于点N
变式1　如图，在矩形ABCD中，AD＝2AB，点E是AD边上一点，且∠BFC＝∠A，求证：BD＝2CE.
证明：∵四边形ABCD是矩形，∴AD＝BC＝2AB＝2CD，∠BCD＝∠ADC＝∠A＝90°，∴∠DBC＋∠BDC＝90°.∵∠BFC＝∠A＝90°，∴∠ECD＋∠BDC＝90°，∴∠DBC＝∠ECD.
解：如图，过点E作EM⊥CD于点M，过点G作GN⊥AD于点N，设EF，GH相交于点O，则EM＝BC，GN＝AB，∵EF⊥GH，∴∠FOH＝90°.∵四边形ABCD是矩形，∴∠D＝90°，
∴∠GHN＋∠EFD＝180°，∵∠EFM＋∠EFD＝180°，∴∠GHN＝∠EFM.∵∠GNH＝∠EMF，∴△GHN∽△EFM，∴ ＝ .