圆-中考数学一轮复习课件

这是一份圆-中考数学一轮复习课件，共60页。PPT课件主要包含了°直角，垂直平分线，例4图，第10题，第11题，且只有一个，三条角平分线，外接圆，圆心角，πr2等内容，欢迎下载使用。

第25课时　圆的相关概念及性质
1. 理解圆、弧、弦、圆心角、圆周角的概念,了解等圆、等弧的概 念.2. 探索并掌握垂径定理及其推论.3. 探索圆周角与圆心角及其所对弧的关系,了解并证明圆周角定理 及其推论.4. 知道三角形的外心,并能画任意三角形的外接圆.
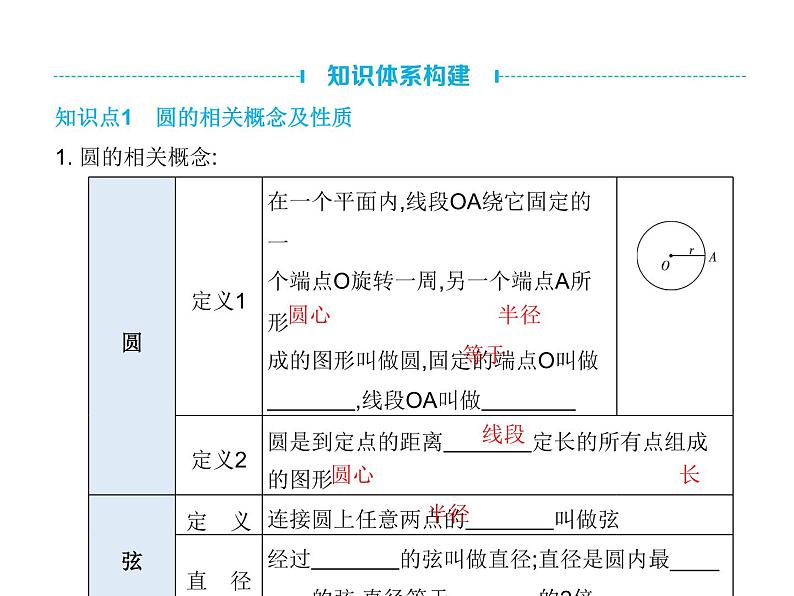
知识点1　圆的相关概念及性质1. 圆的相关概念:
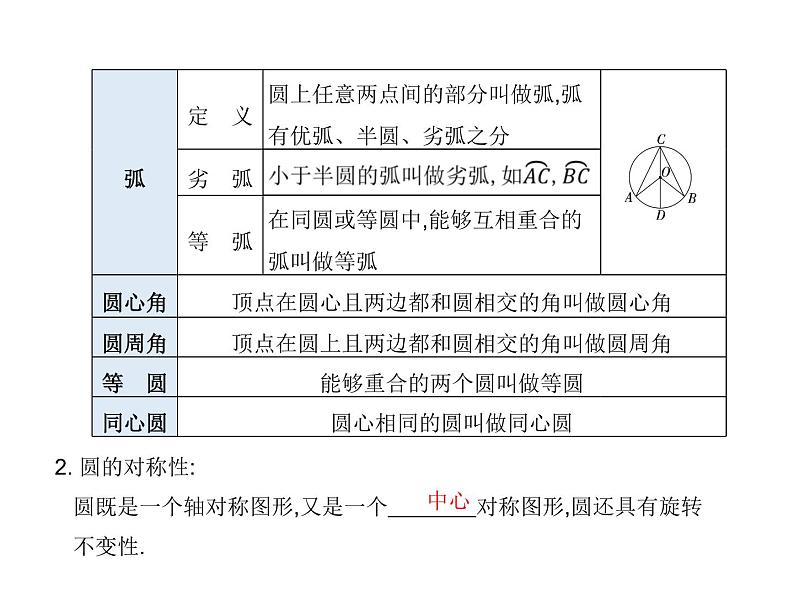
2. 圆的对称性: 圆既是一个轴对称图形,又是一个　　　　对称图形,圆还具有旋转 不变性. 
知识点3　弧、弦、圆心角的关系1. 定理:在同圆或等圆中,相等的圆心角所对的弧　　　　,所对的弦 也　　　　. 2. 推论:在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组 量相等,那么它们所对应的其余各组量都分别　　　　. 
[温馨提示] 弦心距、半径、弦的一半构成的直角三角形,常用于求未知线段的长或角的度数,为构造这个直角三角形,常连接半径或作弦心距,利用勾股定理求未知线段的长.
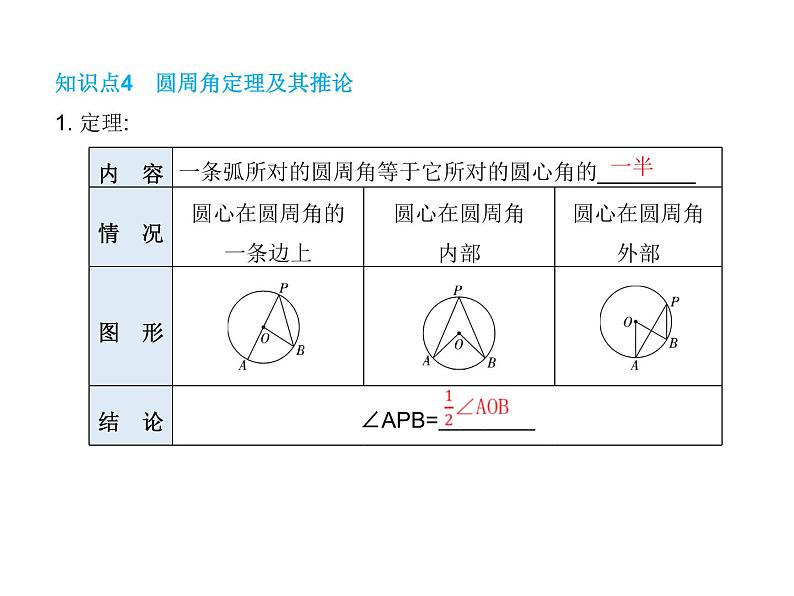
知识点4　圆周角定理及其推论1. 定理:
2. 推论:(1) 推论1:同弧或等弧所对的圆周角　　　　. (2) 推论2:半圆(或直径)所对的圆周角是　　　 　;90°的圆周角所对的弦是　　　　. (3) 推论3:如果三角形一边上的中线等于这边的一半,那么这个三角形是　　　　三角形. 
[温馨提示] 1. 一条弦(不是直径)对着两条弧,分为优弧和劣弧,优弧和劣弧对着的两个圆周角互补;2. 一条弧只对着一个圆心角,但却对着无数个圆周角.
知识点5　圆内接多边形
考点一　垂径定理及其推论例1 (2022·青海)如图①所示为一个隧道的横截面,它的形状是以点O为圆心的圆的一部分,C是☉O中弦AB的中点,CD经过圆心O交☉O于点D.若AB=4m,CD=6m,则☉O的半径长为　　　　m. [思路点拨] 如图②,连接OA,根据垂径定理的推论可得CD⊥AB,在Rt△AOC中,利用勾股定理构造与半径有关的方程,解之即可.
[非常点评] 利用垂径定理及其推论进行计算时,通常是在半径、弦心距和弦的一半所组成的直角三角形中,利用勾股定理直接求或构造方程求出未知线段的长,一般地,在圆中求弦长时往往作弦心距利用垂径定理、勾股定理求解.
[非常点评] 在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等.在运用弧、弦、圆心角之间的关系解决问题时,一定要注意“在同圆或等圆中”这一前提条件,否则结论不一定成立.
考点三　圆周角定理及其推论例3 (2022·兰州)如图,△ABC内接于☉O,CD是☉O的直径.若∠ACD=40°,则∠B的度数为 (　　)A. 70° B. 60° C. 50° D. 40°[思路点拨] 由圆周角定理的推论知∠CAD=90°,利用直角三角形的性质求得∠D的度数,最后利用同弧所对圆周角相等求出∠B的度数.[非常点评] 进行与圆有关的角度的相关计算时,一般先判断角是圆周角还是圆心角,再转化成同弧或等弧所对的圆周角或圆心角,利用同弧或等弧所对的圆周角相等,同弧或等弧所对的圆周角是圆心角的一半等关系求解.
∵ CD是☉O的直径,∴ ∠CAD=90°.∴ ∠ACD+∠D=90°.∵ ∠ACD=40°,∴ ∠D=∠B=90°-40°=50°.故选C.
考点四　圆内接四边形例4 (2022·自贡)如图,四边形ABCD内接于☉O,AB是☉O的直径.若∠ABD=20°,则∠BCD的度数是 (　　)A. 90°B. 100°C. 110°D. 120°[思路点拨] 根据AB是☉O的直径,可以得到∠ADB=90°,再根据∠ABD=20°和三角形内角和定理,可以得到∠A的度数,最后根据圆内接四边形对角互补得到∠BCD的度数.
∵ AB是☉O的直径,∴ ∠ADB=90°.∵ ∠ABD=20°,∴ ∠A=90°-20°=70°.∵ 四边形ABCD是圆内接四边形,∴ ∠A+∠BCD=180°.∴ ∠BCD=180°-70°=110°.故选C.
[非常点评] 解答与圆有关的角的度数的计算问题时,常常要结合“圆内接四边形的性质”及“圆周角定理及其推论”,有时再结合三角形的内角和定理等进行求解.
10. (2022·盐城)请借助如图所示的图形,求证:垂直于弦AB的直径CD平分弦以及弦所对的两条弧.
11. (2021·徐州)如图,AB为☉O的直径,点 C,D在☉O上,AC与OD交于点E,AE=EC,OE=ED.连接BC,CD.求证:(1) △AOE≌△CDE;(2) 四边形OBCD是菱形.
(1) 在△AOE和△CDE中,∵ AE=CE,∠AEO=∠CED,OE=DE,∴ △AOE≌△CDE　(2) ∵ △AOE≌△CDE,∴ AO=CD,∠AOE=∠D.∴ OB∥CD.∵ AO=OB,∴ OB=CD.∴ 四边形OBCD为平行四边形.∵ OB=OD,∴ 四边形OBCD是菱形
第26课时　与圆有关的位置关系
1. 探索并了解点与圆的位置关系,了解直线与圆的位置关系及三角 形内切圆的概念,会判断直线与圆的位置关系.2. 掌握切线的概念,探索切线与过切点的半径的关系,会用三角尺过 圆上一点画圆的切线.3. 探索并证明切线长定理,会利用它进行证明和相关计算.
知识点1　与圆有关的位置关系1. 点和圆的位置关系: 如果设圆的半径为r,点到圆心的距离为d,那么: (1) dr⇔点在　　　　. 
2. 直线和圆的位置关系: 设☉O的半径为r,圆心O到直线l的距离为d. 即:(1) d>r⇔直线l与圆　　　　;  (2) d=r⇔直线l与圆　　　　;  (3) d[温馨提示] 判断直线和圆的位置关系有两种方法:一是根据公共点的个数判断;二是根据圆心到直线的距离与半径的大小关系判断.
知识点2　圆的切线1. 定义:与圆有　　　　 　　公共点的直线叫做圆的切线,唯一的公共 点叫做　　　　. 2. 切线的性质: (1) 圆的切线垂直于经过　　　　的半径;  (2) 经过圆心且垂直于切线的直线经过　　　　;  (3) 经过切点且垂直于切线的直线经过　　　　. 3. 切线的判定: (1) 与圆有　　　　　　公共点的直线是圆的切线;  (2) 如果圆心到一条直线的距离等于圆的　　　　,那么这条直线是 圆的切线;  (3) 经过半径的外端并且　　　　于这条半径的直线是圆的切线. 
知识点3　切线长和切线长定理
知识点4　三角形的内切圆1. 三角形的内切圆:与三角形各边　　　　的圆叫做三角形的内切圆. 这个三角形叫做圆的　　　　三角形. 2. 三角形的内心:内切圆的圆心叫做三角形的　　 　,它是三角形 　　　　　　　　　的交点.三角形的内心到三边的　　　　相等. 
考点一　与圆有关的位置关系例1 (2021·嘉兴)已知平面内有☉O和点A,B,☉O的半径为2cm,线段OA=3cm,OB=2cm,则直线AB与☉O的位置关系为 (　　)A. 相离 B. 相交C. 相切 D. 相交或相切[非常点评] 本题是直线与圆位置关系的应用,要判断直线与圆的位置关系,在已知圆的半径的前提下,只要求出圆心到直线的距离,与半径比较大小即可判断.设圆心到直线的距离为d,圆的半径为r.若dr,则直线与圆相离.
∵ ☉O的半径为2cm,线段OA=3cm,OB=2cm,∴ 点A到圆心O的距离大于圆的半径,点B到圆心O的距离等于圆的半径.∴ 点A在☉O外,点B在☉O上.∴ 易得直线AB与☉O的位置关系为相交或相切.故选D.
考点二　切线的性质与判定例2 (2022·泰州)如图①,PA与☉O相切于点A,PO与☉O相交于点B,点C在优弧AB上,且不与点A,B重合.若∠P=26°,则∠C的度数为　　　　. [思路点拨] 如图②,连接OA,由PA与☉O相切于点A,可得∠OAP=90°,从而根据∠P的度数求出∠AOB的度数,再根据圆周角定理求出∠C的度数.[非常点评] 看到圆的切线就应想到过切点的半径与切线垂直,从而为求角度或勾股定理的应用进行铺垫.
例3 (2022·衡阳)如图,AB为☉O的直径,过圆上一点D作☉O的切线CD,交BA的延长线于点C,过点O作OE∥AD交CD的延长线于点E,连接BE.(1) 直线BE与☉O相切吗?请说明理由.(2) 若CA=2,CD=4,求DE的长. [思路点拨] (1) 连接OD,由切线的性质可得∠ODE=90°,然后利用平行线和等腰三角形的性质可得∠DOE=∠EOB,进而可证△DOE≌△BOE,最后利用全等三角形的性质证得∠OBE=90°解决问题;(2) 设☉O的半径为r,先在Rt△ODC中,利用勾股定理求出r的长,再利用(1)的结论可得DE=BE,最后在Rt△BCE中,利用勾股定理进行计算即可解答.
(1) 直线BE与☉O相切.理由:如图,连接OD.∵ CD与☉O相切于点D,∴ ∠ODE=90°.∵ AD∥OE,∴ ∠ADO=∠DOE,∠DAO=∠EOB.∵ OD=OA,∴ ∠ADO=∠DAO.∴ ∠DOE=∠EOB.∵ OD=OB,OE=OE,∴ △DOE≌△BOE.∴ ∠ODE=∠OBE=90°.∵ OB是☉O的半径,∴ 直线BE与☉O相切.(2) 设☉O的半径为r.在Rt△ODC中,OD2+DC2=OC2,∴ r2+42=(r+2)2,解得r=3.∴ AB=2r=6.∴ BC=AC+AB=2+6=8.由(1),得△DOE≌△BOE,∴ DE=BE.在Rt△BCE中,BC2+BE2=CE2,∴ 82+BE2=(4+DE)2.∴ 64+DE2=(4+DE)2.∴ DE=6.∴ DE的长为6.
[方法归纳] 判定圆的切线的常见思路 (1) 若已知直线与圆的公共点,则采用判定定理法,其基本思路是当已知点在圆上时,连接过这点的半径,证明这条半径与直线垂直即可,可简述为有切点,连半径,证垂直;(2) 若未知直线与圆的公共点,则采用数量关系法,其基本思路是过圆心作直线的垂线段,证明垂线段的长等于圆的半径,可简述为无切点,作垂线,证相等.
考点三　切线长定理与内切圆例4 (2022·眉山)如图所示为不倒翁的主视图,不倒翁的圆形脸恰好与帽子边沿PA,PB分别相切于点A,B,不倒翁的鼻尖正好是圆心O.若∠OAB=28°,则∠APB的度数为 (　　) A. 28° B. 50° C. 56° D. 62°[思路点拨] 由☉O与PA,PB分别相切于点A,B可知PA=PB,∠OAP=90°,又因为∠OAB=28°,从而可求得∠PAB的度数,最后利用三角形内角和定理及等腰三角形的性质求解即可.
[非常点评] 过圆外一点引圆的两条切线,根据切线长定理可得有关线段与角的结论,进而为解决其他问题打下基础.
∵ ☉O与PA,PB分别相切于点A,B,∴ PA=PB,∠OAP=90°.∴ ∠PAB=∠PBA.∵ ∠OAB=28°,∴ ∠PAB=90°-28°=62°.∴ ∠APB=180°-2∠PAB=180°-124°=56°.故选C.
例5 (2021·毕节)如图,☉O是△ABC的外接圆,点E是△ABC的内心,AE的延长线交BC于点F,交☉O于点D,连接BD,BE.(1) 求证:DB=DE;(2) 若AE=3,DF=4,求DB的长. [思路点拨] (1) 依据三角形内心的性质可得∠BAD=∠CAD,∠ABE=∠CBE,由圆周角定理的推论可得∠CAD=∠CBD=∠BAD,从而可证∠BED=∠DBE,根据等角对等边即可得结论;(2) 由∠D=∠D,∠BAD=∠FBD,可得△ABD∽△BFD,进而由相似三角形性质构造方程,从而可求DB的长.
[非常点评] 本题考查了三角形内心的性质、圆周角定理的推论,相似三角形的判定与性质,根据三角形内心的性质证得△ABD∽△BFD是解题的关键.
5. (2022·连云港)如图,AB是☉O的直径,AC是☉O的切线,A 为切点,连接 BC,与☉O交于点D,连接OD.若∠AOD=82°,则∠C的度数是　　　　. 6. (2022·秦淮二模)如图,☉O是△ABC的内切圆,与AB,BC,CA的切点分别 为D,E,F.若∠BDE+∠CFE=110°,则∠A的度数是　　　　. 7. (2021·泰州)如图,在平面直角坐标系中,点A的坐标为(8,5),☉A与x 轴相切,点P在y轴正半轴上,PB与☉A相切于点B.若∠APB=30°,则点P 的坐标为　　　　　　. 8. 如图所示的网格是由边长为1个单位长度的小正方形组成的,已知点A, B,C在平面直角坐标系中的坐标分别为(3,6),(-3,3),(7,-2),则△ABC 内心的坐标为　　　　. 
9. (2022·安徽)已知AB为☉O的直径,C为☉O上一点,D为BA的延长线上一点,连接CD.(1) 如图①,若CO⊥AB,∠D=30°,OA=1,求AD的长;(2) 如图②,若DC与☉O相切,E为OA上一点,且∠ACD=∠ACE,求证:CE⊥AB.
10. (2022·广元)如图,在Rt△ABC中,∠ACB=90°,以AC为直径的☉O交AB于点D,E是边BC的中点,连接DE.(1) 求证:DE是☉O的切线;(2) 若AD=4,BD=9,求☉O的半径.
(1) 如图①,连接OD,OE.∵ OA=OD,∴ ∠A=∠ODA.∵ E是边BC的中点,OA=OC,∴ OE∥AB.∴ ∠DOE=∠ODA,∠A=∠COE.∴ ∠COE=∠DOE.∵ OC=OD,OE=OE,∴ △COE≌△DOE.∵ ∠ACB=90°,∴ ∠ODE=∠ACB=90°.∵ OD为☉O的半径,∴ DE是☉O的切线　
第27课时　与圆有关的计算
1. 了解正多边形的概念及正多边形与圆的关系,能将正多边形问题 转化为三角形问题.2. 会计算扇形的弧长、面积及组合图形的周长与面积.3. 理解圆柱、圆锥的侧面展开图,掌握圆柱、圆锥的侧面积和全面 积的计算方法.
知识点1　正多边形和圆
知识点2　弧长及扇形面积的相关计算
[温馨提示] 1. 如果题目中没有明确给出精确度,可用含“π”的数表示弧长;2. 应区分弧、弧长这两个概念,弧长相等的弧不一定是等弧.
知识点3　圆锥的侧面积和全面积
考点一　与正多边形有关的计算例1 (2022·株洲)如图,∠MON=60°,正五边形ABCDE的顶点A,B在射线OM上,顶点E在射线ON上,则∠AEO的度数为　　　　.  
[误区警示] 此类问题容易出错的地方,一是不知道几何体的侧面展开图与几何体各个部分之间的关联,二是没有掌握相关的计算公式.圆锥的侧面展开图的相关公式:S圆锥侧=πrl,S圆锥全=πrl+πr2.其中r为底面圆的半径,l为母线长.
例6 (2022·玄武二模)如图,沿一条母线将圆锥侧面剪开并展平,得到一个扇形.若扇形的半径R=6cm,扇形的圆心角θ=120°,则该圆锥的高为　　　　cm. [非常点评] 圆锥的侧面展开图是扇形,要注意扇形与圆锥的联系:扇形的弧长等于圆锥底面圆的周长,扇形的半径等于圆锥的母线长.
[非常点评] 对于此类求不规则图形的面积的题目,关键是将不规则图形转化为规则图形,常通过直接和差、平移、旋转、分割等方法,把不规则图形的面积转化为规则图形面积的和或差,如本题中将阴影部分的面积转化为扇形面积与三角形面积的差.
例8 (2022·宿迁)如图,在△ABC中,∠ABC=45°,AB=AC,以AB为直径的☉O与边BC交于点D.(1) 判断直线AC与☉O的位置关系,并说明理由;(2) 若AB=4,求图中阴影部分的面积.[思路点拨] (1) 根据等腰三角形的性质和三角形内角和定理可得∠BAC=90°,从而可得结论;(2) 连接OD,AD,根据图中阴影部分的面积=S△ABC-S△BOD-S扇形AOD可求得结果.
(1) 直线AC与☉O相切.理由:∵ ∠ABC=45°,AB=AC,∴ ∠ABC=∠C=45°.∴ ∠BAC=180°-2×45°=90°.∴ BA⊥AC.∵ AB是☉O的直径,∴ 直线AC与☉O相切.
[非常点评] 证明直线与圆相切时,若题中说明了直线与圆有交点,则连接交点与圆心,证明半径垂直于直线即可判定直线是圆的切线;若题中没有说明直线与圆有交点,则过圆心作直线的垂线段,证明垂线段的长等于圆的半径也可判定直线是圆的切线.当所求阴影部分的面积是不规则图形的面积时,可将不规则图形转化为规则图形或几个规则图形的组合来计算阴影部分的面积.
1. (2022·湖北)一个扇形的弧长是10πcm,其圆心角是150°,此扇形的 面积为 (　　) A. 30πcm2B. 60πcm2 C. 120πcm2D. 180πcm22. (2022·无锡)在Rt△ABC中,∠C=90°,AC=3,BC=4,以AC所在直线为轴, 把△ABC旋转1周,得到圆锥,则该圆锥的侧面积为 (　　) A. 12πB. 15π C. 20πD. 24π