

中考复习数学隐圆小专题课件
展开模型二:动点+定点(圆心)=定长(半径)
模型一:直角对定弦(直径)
模型四:四点共圆(利用圆内接四边形对角互补)
模型三:定角(圆周角)+定长(弦长)
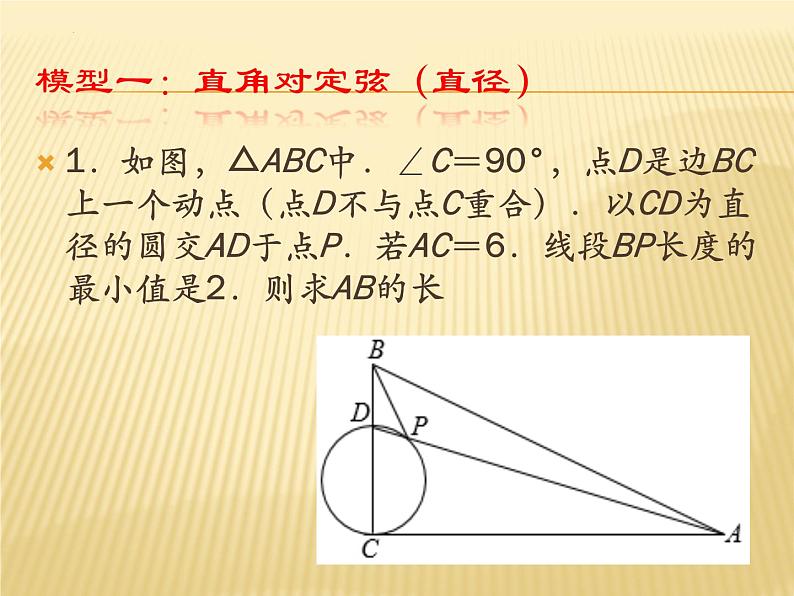
1.如图,△ABC中.∠C=90°,点D是边BC上一个动点(点D不与点C重合).以CD为直径的圆交AD于点P.若AC=6.线段BP长度的最小值是2.则求AB的长
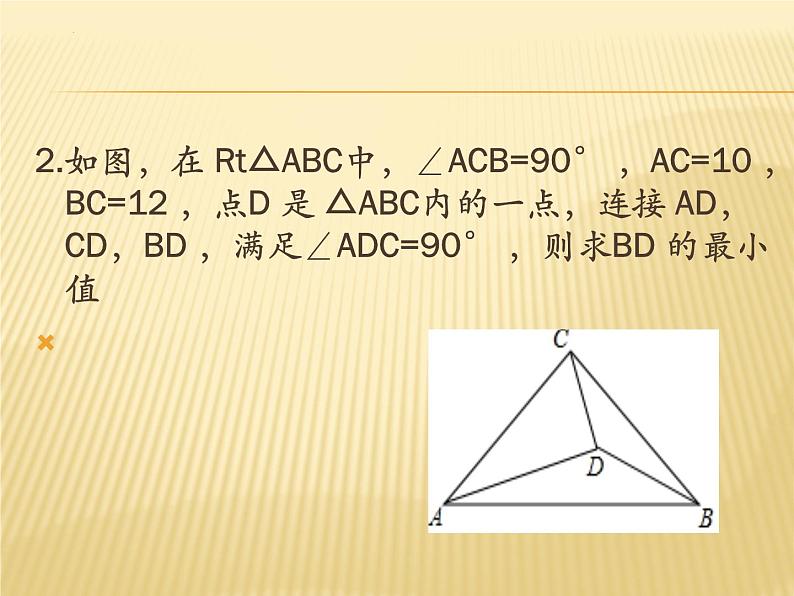
2.如图,在 Rt△ABC中,∠ACB=90° ,AC=10 ,BC=12 ,点D 是 △ABC内的一点,连接 AD, CD,BD ,满足∠ADC=90° ,则求BD 的最小值
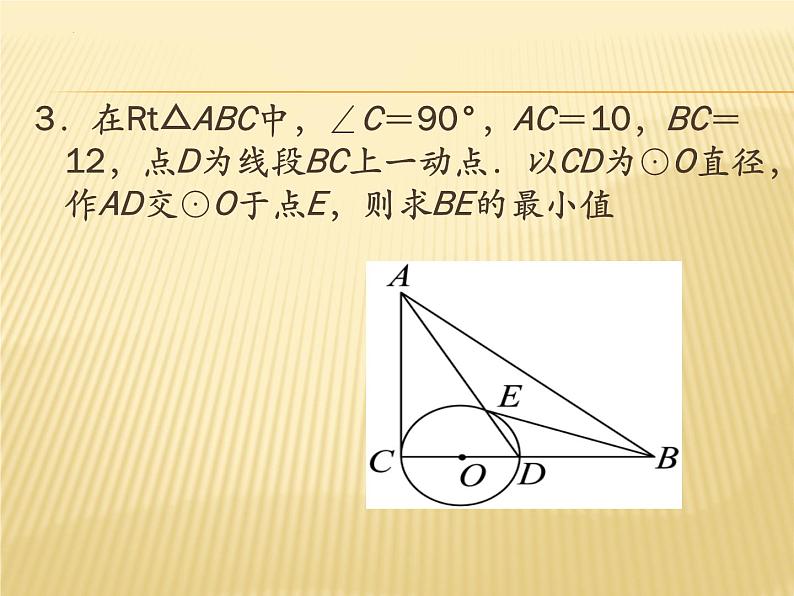
3.在Rt△ABC中,∠C=90°,AC=10,BC=12,点D为线段BC上一动点.以CD为⊙O直径,作AD交⊙O于点E,则求BE的最小值
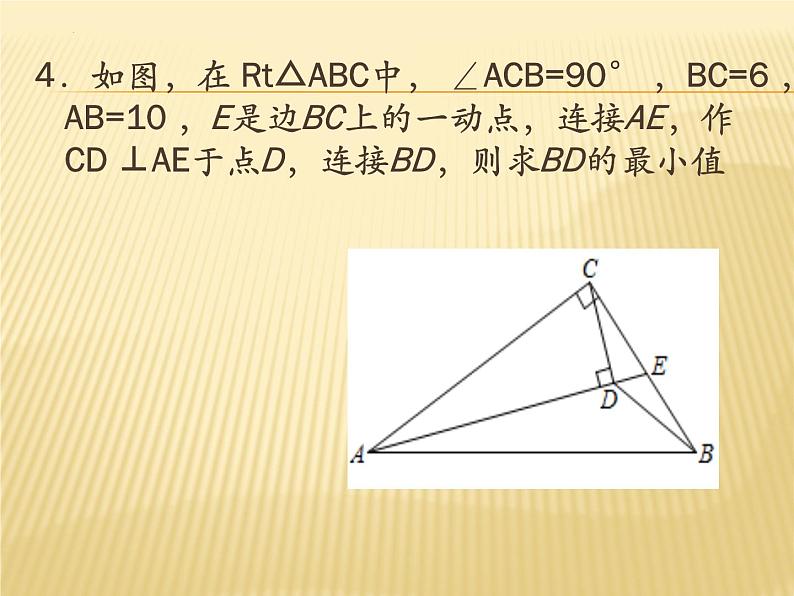
4.如图,在 Rt△ABC中, ∠ACB=90° ,BC=6 ,AB=10 ,E是边BC上的一动点,连接AE,作 CD ⊥AE于点D,连接BD,则求BD的最小值
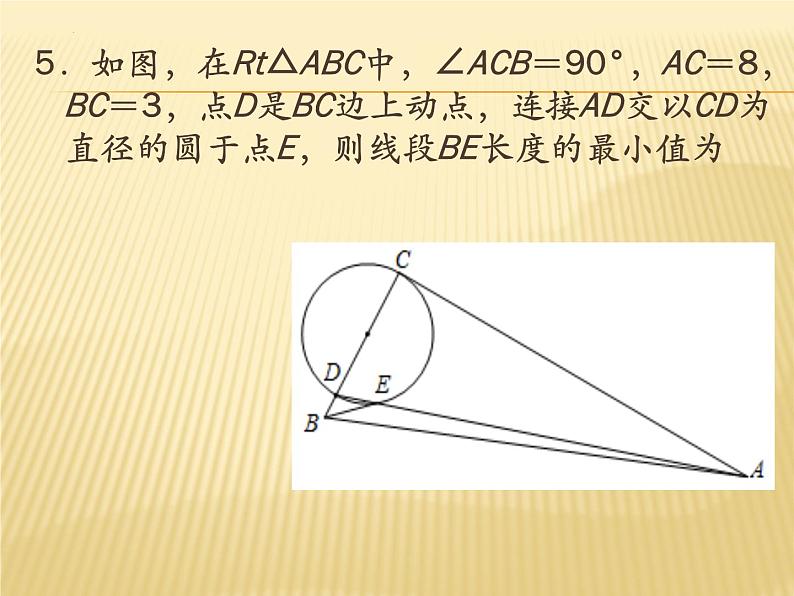
5.如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=3,点D是BC边上动点,连接AD交以CD为直径的圆于点E,则线段BE长度的最小值为
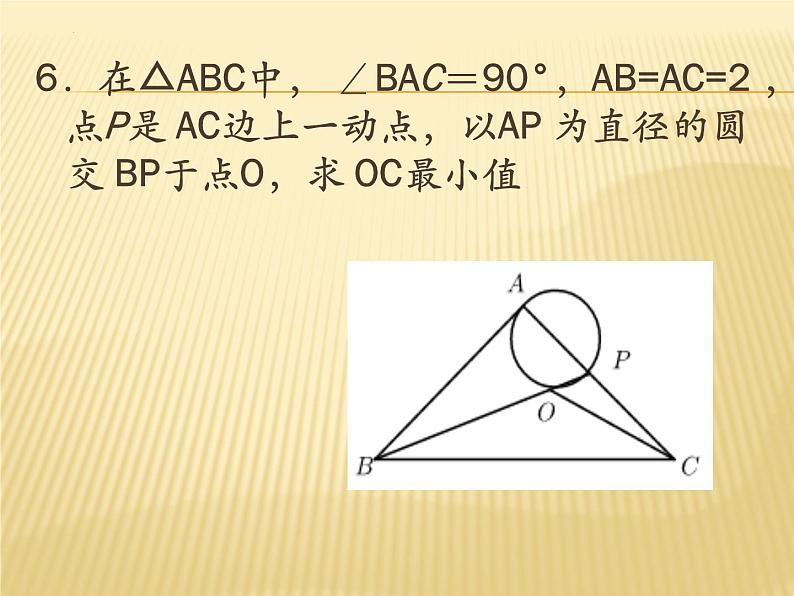
6.在△ABC中, ∠BAC=90°,AB=AC=2 ,点P是 AC边上一动点,以AP 为直径的圆交 BP于点O,求 OC最小值
1.如图,一架梯子靠在墙角,梯子长5米,在沿着墙角缓慢下滑直至水平地面的过程中,梯子的中点P的移动轨迹长度为__;
模型三:定角(圆周角)+定长(弦长)
1.如图,P为等边△ABC外的一个动点(P点与A点分别在BC所在直线的不同侧),且∠APB=60°,AB=1,则求PB+PC的最大值
2.如图,在△ABC中,AC=4 ,BC=6 ,∠ACB=30° ,D是△ABC内一动点,⊙O为 的外接圆,圆O交直线BD于点P,交边BC于点E,若,AE=CP,则求AD的最大值
3.如图,在△ABC中,AC=3 , , ∠ACB=60°,过点A作BC的平行线l,P为直线l上一动点,⊙O为△APC的外接圆,直线BP交⊙O于E点,则求AE的最小值
4.如图,等边△ABC中,AB=3 ,点D,点E分别是边BC,CA上的动点,且 BD=CE,连接AD、BE交于点F,当点D从点B运动到点C时,则点F的运动路径的长度
5.如图,边长为4的正三角形ABC,点M,N分别是边AB,AC上的动点,连接BN,CM交于点P.若BN=CM,当点M由点B运动到点A时,点P所经过的路径长为
模型四:四点共圆(利用圆内接四边形对角互补)
1.如图,正方形ABCD的边长为4,点E是正方形外一动点,且点E在CD的右侧,∠AED=45° ,P为AB的中点,当E运动时,求线段PE的最大值
2.如图, 是Rt△ABC和 Rt △ABD的公共斜边,AC=BC, ∠BAD=32° ,E是 的中点,联结DE、CE、CD,求 ∠ECD度数。
3.如图所示,AB=AC=AD , ∠BAC=60° ,求∠BDC
4.在Rt△ABC中, ∠ACB=90° ,AC=4,D为平面内一点,连接AD ,CD. ∠ADC=30°,则求线段BD 的最小值
模型五:定角定高(补充)
1.解答题(求面积最大值)(1)如图1,在△ABC中,BC=8,D为BC上一点,AD=6,则△ABC面积的最大值是 ;(2)如图2,在在△ABC中,∠BAC=60°,AG为BC边上的高,⊙O为在△ABC的外接圆,若AG=3,试判断BC是否存在最小值?若存在,请求出最小值;若不存在,请说明理由。
(3)如图3,王先生有一块矩形地ABCD, , 现在他想利用这块地建一个四边形鱼塘AMFN,且满足点E在CD上,AD=DE,点F在BC上,且CF=6,点M在AE上,点N在AB上,∠MFN=90°,这个四边形AMFN的面积是否存在最大值?若存在,求出面积大的最大值;若不存在,请说明理由。
小瓜豆+隐圆+一箭穿心
1.如图,AB是⊙O的直径,C是圆上一点,且∠AOC=120°,⊙O的半径为2,P为圆上的一动点,Q为AP的中点,则求CQ的长的最大值
2.如图,点A,B的坐标分别为A(2,0),B(0,2).点C为平面内一点且BC=1,点M为线段AC的中点,连接OM,则求OM的最大值
3.如图,在正方形ABCD中,AB=4,G是BC的中点,点E是正方形内一个动点,且EG=2,连接DE,将线段DE绕点D逆时针旋转90°得到线段DF,连接CF,则求线段CF长的最小值
1.如图,平面直角坐标系xOy中,点A的坐标为(8,5),⊙A与x轴相切,点P在y轴正半轴上,PB与⊙A相切于点B.若∠APB=30°,则点P的坐标为 _ __.
2.如图,直线 与坐标轴交于A,B两点,已知⊙O的半径为2,若P是⊙O上的一个动点,则求△ABP面积的最大值。
如图,在Rt△AOB中, , ∠A=30°, ⊙O 的半径为1, 点P 是 边AB上的动点,过点 P作⊙O的一条切线 PQ(其中点Q 为切点),则求线段 PQ长度的最小值
中考数学复习微专题五圆中经典模型——隐圆问题模型四四点共圆课件: 这是一份中考数学复习微专题五圆中经典模型——隐圆问题模型四四点共圆课件,共12页。PPT课件主要包含了基本模型,针对训练,针对巩固等内容,欢迎下载使用。
中考数学复习微专题五圆中经典模型——隐圆问题模型三直角所对的是直径课件: 这是一份中考数学复习微专题五圆中经典模型——隐圆问题模型三直角所对的是直径课件,共8页。PPT课件主要包含了基本模型,针对训练,针对巩固等内容,欢迎下载使用。
中考数学复习微专题五圆中经典模型——隐圆问题模型二动点到定点定长课件: 这是一份中考数学复习微专题五圆中经典模型——隐圆问题模型二动点到定点定长课件,共8页。PPT课件主要包含了基本模型,针对训练,针对巩固等内容,欢迎下载使用。












